基于mit6.006的作业解析

发表于 更新于 分类于 ， 阅读次数： 本文字数： 3.3k 阅读时长 ≈ 12 分钟

hw1

时间复杂度分析

对这种形式的函数可以这样比较

\[f_1=n^{\sqrt{n}}=(2^{lgn})^{\sqrt{n}}\] \[f_2=n^{10}.2^{n/2}=2^{lg(10n)+n/2}\]

复杂度计算

对于T(n,n): T (x, y) = Θ(x + y) + T (x/2, y/2). 化成

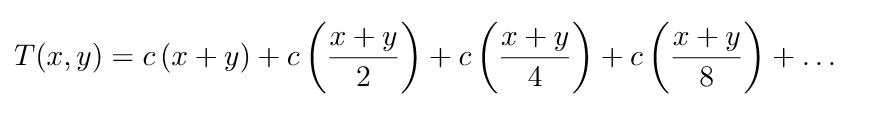
得到θ(n)

T (x, y) = Θ(x) + T (x, y/2). 等于lgy个θ(x) 即，θ(nlgn)

T (x, y) = Θ(x) + S(x, y/2), S(x, y) = Θ(y) + T (x/2, y).

化成T (x, y) = Θ(x) + Θ(y/2) + T (x/2, y/2). 与第一个例子相似，θ(n)

寻峰算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
def algorithm1(problem, trace = None):
    # if it's empty, we're done
    if problem.numRow <= 0 or problem.numCol <= 0:
        return None
    # the recursive subproblem will involve half the number of columns
    mid = problem.numCol // 2
    # information about the two subproblems
    (subStartR, subNumR) = (0, problem.numRow)
    (subStartC1, subNumC1) = (0, mid)
    (subStartC2, subNumC2) = (mid + 1, problem.numCol - (mid + 1))
    subproblems = []
    subproblems.append((subStartR, subStartC1, subNumR, subNumC1))
    subproblems.append((subStartR, subStartC2, subNumR, subNumC2))
    # get a list of all locations in the dividing column
    divider = crossProduct(range(problem.numRow), [mid])
    # find the maximum in the dividing column
    bestLoc = problem.getMaximum(divider, trace)
    # see if the maximum value we found on the dividing line has a better
    # neighbor (which cannot be on the dividing line, because we know that
    # this location is the best on the dividing line)
    neighbor = problem.getBetterNeighbor(bestLoc, trace)
    # this is a peak, so return it
    if neighbor == bestLoc:
        if not trace is None: trace.foundPeak(bestLoc)
        return bestLoc
    # otherwise, figure out which subproblem contains the neighbor, and
    # recurse in that half
    sub = problem.getSubproblemContaining(subproblems, neighbor)
    if not trace is None: trace.setProblemDimensions(sub)
    result = algorithm1(sub, trace)
    return problem.getLocationInSelf(sub, result)
def algorithm2(problem, location = (0, 0), trace = None):
    # if it's empty, we're done
    if problem.numRow <= 0 or problem.numCol <= 0:
        return None
    nextLocation = problem.getBetterNeighbor(location, trace)
    if nextLocation == location:
        # there is no better neighbor, so return this peak
        if not trace is None: trace.foundPeak(location)
        return location
    else:
        # there is a better neighbor, so move to the neighbor and recurse
        return algorithm2(problem, nextLocation, trace)
def algorithm3(problem, bestSeen = None, trace = None):
    # if it's empty, we're done
    if problem.numRow <= 0 or problem.numCol <= 0:
        return None
    midRow = problem.numRow // 2
    midCol = problem.numCol // 2
    # first, get the list of all subproblems
    subproblems = []
    (subStartR1, subNumR1) = (0, midRow)
    (subStartR2, subNumR2) = (midRow + 1, problem.numRow - (midRow + 1))
    (subStartC1, subNumC1) = (0, midCol)
    (subStartC2, subNumC2) = (midCol + 1, problem.numCol - (midCol + 1))
    subproblems.append((subStartR1, subStartC1, subNumR1, subNumC1))
    subproblems.append((subStartR1, subStartC2, subNumR1, subNumC2))
    subproblems.append((subStartR2, subStartC1, subNumR2, subNumC1))
    subproblems.append((subStartR2, subStartC2, subNumR2, subNumC2))
    # find the best location on the cross (the middle row combined with the
    # middle column)
    cross = []
    cross.extend(crossProduct([midRow], range(problem.numCol)))
    cross.extend(crossProduct(range(problem.numRow), [midCol]))
    crossLoc = problem.getMaximum(cross, trace)
    neighbor = problem.getBetterNeighbor(crossLoc, trace)
    # update the best we've seen so far based on this new maximum
    if bestSeen is None or problem.get(neighbor) > problem.get(bestSeen):
        bestSeen = neighbor
        if not trace is None: trace.setBestSeen(bestSeen)
    # return if we can't see any better neighbors
    if neighbor == crossLoc:
        if not trace is None: trace.foundPeak(crossLoc)
        return crossLoc
    # figure out which subproblem contains the largest number we've seen so
    # far, and recurse
    sub = problem.getSubproblemContaining(subproblems, bestSeen)
    newBest = sub.getLocationInSelf(problem, bestSeen)
    if not trace is None: trace.setProblemDimensions(sub)
    result = algorithm3(sub, newBest, trace)
    return problem.getLocationInSelf(sub, result)
def algorithm4(problem, bestSeen = None, rowSplit = True, trace = None):
    # if it's empty, we're done
    if problem.numRow <= 0 or problem.numCol <= 0:
        return None
    subproblems = []
    divider = []
  
    if rowSplit:
        # the recursive subproblem will involve half the number of rows
        mid = problem.numRow // 2
  
        # information about the two subproblems
        (subStartR1, subNumR1) = (0, mid)
        (subStartR2, subNumR2) = (mid + 1, problem.numRow - (mid + 1))
        (subStartC, subNumC) = (0, problem.numCol)
  
        subproblems.append((subStartR1, subStartC, subNumR1, subNumC))
        subproblems.append((subStartR2, subStartC, subNumR2, subNumC))
  
        # get a list of all locations in the dividing column
        divider = crossProduct([mid], range(problem.numCol))
    else:
        # the recursive subproblem will involve half the number of columns
        mid = problem.numCol // 2
  
        # information about the two subproblems
        (subStartR, subNumR) = (0, problem.numRow)
        (subStartC1, subNumC1) = (0, mid)
        (subStartC2, subNumC2) = (mid + 1, problem.numCol - (mid + 1))
  
        subproblems.append((subStartR, subStartC1, subNumR, subNumC1))
        subproblems.append((subStartR, subStartC2, subNumR, subNumC2))
  
        # get a list of all locations in the dividing column
        divider = crossProduct(range(problem.numRow), [mid])
  
    # find the maximum in the dividing row or column
    bestLoc = problem.getMaximum(divider, trace)
    neighbor = problem.getBetterNeighbor(bestLoc, trace)
  
    # update the best we've seen so far based on this new maximum
    if bestSeen is None or problem.get(neighbor) > problem.get(bestSeen):
        bestSeen = neighbor
        if not trace is None: trace.setBestSeen(bestSeen)
  
    # return when we know we've found a peak
    if neighbor == bestLoc and problem.get(bestLoc) >= problem.get(bestSeen):
        if not trace is None: trace.foundPeak(bestLoc)
        return bestLoc
  
    # figure out which subproblem contains the largest number we've seen so
    # far, and recurse, alternating between splitting on rows and splitting
    # on columns
    sub = problem.getSubproblemContaining(subproblems, bestSeen)
    newBest = sub.getLocationInSelf(problem, bestSeen)
    if not trace is None: trace.setProblemDimensions(sub)
    result = algorithm4(sub, newBest, not rowSplit, trace)
    return problem.getLocationInSelf(sub, result)

算法一二如课程笔记所述，均是正确的，以下是证明

  • algo1
  1. 证明算法不可能返回一个空值，首先算法不可能得到一个负索引的子数组（在只有一列的时候必然会得到结果而不是继续划分），在最小问题的情况下，如果此时子问题有一列，那么必然返回一个峰值，如果有两列，不管目前讨论的列是不是最大值，都会递归成最小为1为列的子问题，不会返回空值
  2. 证明返回的位置确实是峰值位置，如果算法1返回一个位置（r1，c1），则该位置必须具有列c1中的最大值，并且必须是某个递归子问题中的峰值。为了推导矛盾，假设（r1，c1）不是原始问题中的峰值。在某个子问题中，位置（r1，c1）与列c2相邻（|c1 - c2| = 1），并且值必须满足不等式val（r1，c1）< val（r1，c2）。
    让（r2，c2）是算法1在c2列中找到的最大值的位置。因此，必定有val（r1，c2）≤ val（r2，c2）。因为c2是分割线，且算法选择在包含（r1，c1）的一半上进行递归，所以我们知道val（r2，c2）< val（r2，c1）。因此，我们有以下不等式链：
    val（r1，c1）< val（r1，c2）≤ val（r2，c2）< val（r2，c1）
    但是，为了使算法1将（r1，c1）作为峰值返回，（r1，c1）处的值必须是其列中的最大值，即val（r1，c1）≥ val（r2，c1）。因此，我们得到了一个矛盾。
  • algo3是错误的

时间复杂度是θ(n)，情况类似复杂度题目的第一个情况，1+1/2+1/4……

反例

如图所示的反例会选择返回一个在当前子问题中看起来像一个峰值，但是与子问题外部的某个更大值相邻的位置

0 0 9 8 0 0 0
0 0 0 0 0 0 0
0 1 0 0 0 0 0
0 2 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0

对算法四的证明

  • algo4

时间复杂度是θ(n),类似算法3

算法四交叉进行行和列的最大值寻找

  1. 如果峰值问题不为空，则算法将始终返回一个位置。在算法中，根据是在行还是列上分割，递归子问题的维度会相应地减少。所以算法要么在某个时刻停止并返回一个位置，要么最终检查一个行数或列数为非正的子问题。但是，问题的行数或列数变为严格负数的唯一方式是在某个时刻m=0或n=0。因此，如果算法没有返回位置，它必定最终检查一个空的子问题。然而，证明假设该情况不会发生。
  2. 如果算法返回一个位置，则该位置将是原始问题中的一个峰值。如果算法返回一个位置(r1, c1)，那么该位置必定是某个递归子问题中的峰值。另外，如果(r2, c2)是算法执行过程中的最佳位置（存储在bestSeen变量中的位置），那么必定满足val(r1, c1) ≥ val(r2, c2)。证明假设(r1, c1)不是原始问题的峰值。那么当位置(r1, c1)通过递归调用链向上传递时，它必定在某个级别停止是不是峰值。因此，必定存在一个包含位置(r1, c1)的子问题，在该级别中，该子问题的某个邻居(r3, c3)的值满足val(r1, c1) < val(r3, c3)。对于(r3, c3)既是递归子问题的邻居又不包含在子问题中，它必定在算法的执行过程中被检查过。因此，必定满足val(r3, c3) ≤ val(r2, c2)。因此，我们得到以下不等式链：val(r1, c1) < val(r3, c3) ≤ val(r2, c2) ≤ val(r1, c1)。这导致了矛盾。

hw2

科赫雪花

简单的演示
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
SNOWFLAKE(n)
 e1, e2, e3 = edges of an equilateral triangle with side length 1
 SNOWFLAKE-EDGE(e1, n)
 SNOWFLAKE-EDGE(e2, n)
 SNOWFLAKE-EDGE(e3, n)
SNOWFLAKE-EDGE(edge, n)
 if n = = 0
  edge is an edge on the snowflake
 else
  e1, e2, e3 = split edge in 3 equal parts
 SNOWFLAKE-EDGE(e1, n − 1)
 f2, g2 = edges of an equilateral triangle whose 3rd edge is e2, pointing outside the snowflake
 ∆(f2, g2, e2) is a triangle on the snowflake’s surface
 SNOWFLAKE-EDGE(f2, n − 1)
 SNOWFLAKE-EDGE(g2, n − 1)
 SNOWFLAKE-EDGE(e3, n − 1)

从主函数（层数视为-1)开始对每条边进行处理，这一层有三个节点。 而对边处理的函数则遵从这样的流程

  1. 把边等分成三个部分e1,e2,e3
  2. 对e1进行递归
  3. 以e2为一条边向外侧生成一个等边三角形，f2,g2是这个三角形的另外两条边
  4. 以此对f2,g2,e3进行递归 函数实际上把一条边拓展出了一个三角形 因此第i层的节点数是:\[3*4^i\]

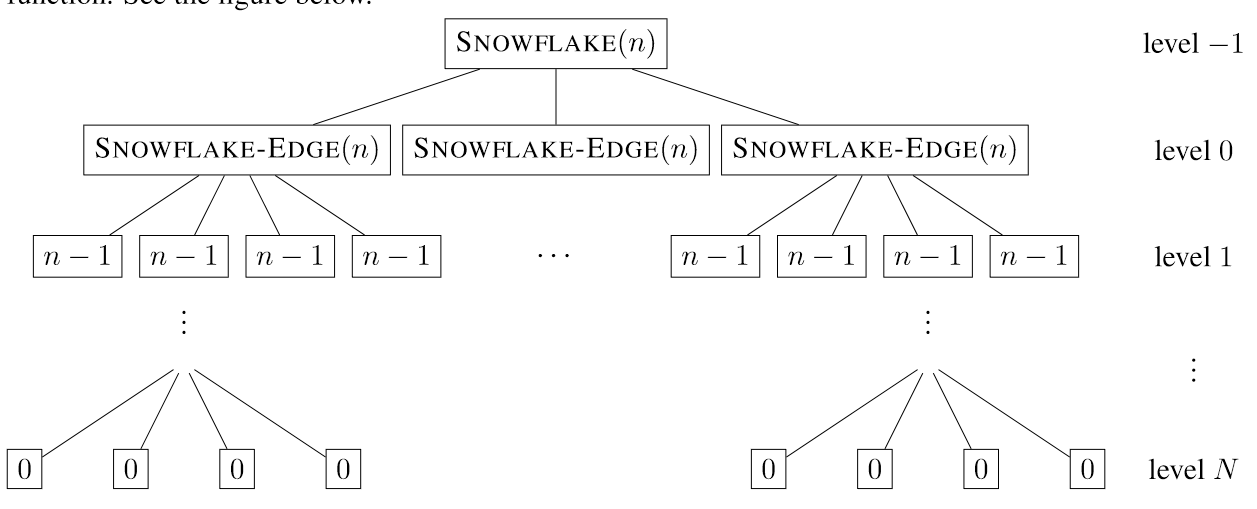
3D 硬件加速渲染

在这种渲染方式中，cpu计算分解出的三角形顶点的集合，发给gpu进行绘制，因此cpu的执行时间只取决于分解出的三角形数量，也就是θ(4^n)

2D 硬件加速渲染

在这种渲染方式中，cpu实际上只计算不断分割出的线段集合，在本题中就是计算最外侧的轮廓的顶点的集合，计算结束后发给gpu绘制 时间复杂度依旧是θ(4^n)，但需要注意的是由于计算完了才开始渲染，因此递归树的中间节点不会对渲染产生时间消耗

软件渲染

在没有硬件加速器的2D渲染（也称为软件渲染）中，CPU 像上一部分一样，为每个路径编译一个线段列表，但它也负责 用于“光栅化”每个线段。 光栅化获取线段端点的坐标 并计算位于线段上的所有像素的坐标。 用这些像素在显示器上绘制线段。光栅化算法在时间上的消耗与线段的长度成正比，线段上的像素数量与线段的长度成正比。 在整个问题中，假设所有线段的长度至少为一个像素，因此 光栅化的成本大于编译线段的成本。 需要注意的是：

  1. 中间节点依旧对渲染无影响
  2. 由于每次对边处理实际上增加了该边1/3的像素点，所以最后一层产生的代价是\[θ({(1/3)}^n)\]
  3. 同理，总渲染代价和cpu处理（只处理像素点）的时间复杂度都是\[θ({(4/3)}^n)\]

没有硬件加速的 3D 渲染

在这种情况下， CPU 编译三角形列表，然后光栅化每个三角形。 我们知道一种算法 栅格化一个三角形，其运行时间与三角形的表面积成正比。三角形内的像素数量与三角形的面积成正比。可以假设边长为 l 的三角形的面积为 θ(l^2)。 顺着递归树进行分析，首层只增加了三个节点，每个新节点对应一个边长是原边长1/3的新三角形，增加了1/3的面积，之后的每一层都有4^i个节点，对应4/9的面积增长，即每层的增长是 \[\frac{1}{3}.\frac{4}{9}^i\] 可以用等比数列的求和算出答案，但时间复杂度必然是θ(1)

电路模拟

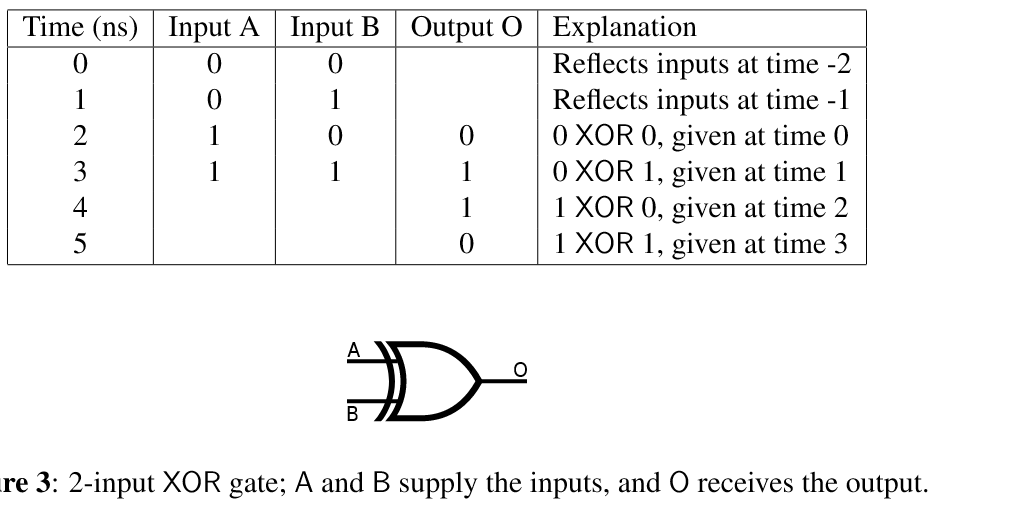如图是对一个异或门的模拟，两个输入端AB产生的信号会在2ns的延迟后在输出端产生一个结果，除此以外没有延迟 按照题意运行python -m cProfile -s time circuit.py < tests/5devadas13.in 得到如下结果（不完全），可以看到消耗最多时间的是lt(lower than)和find_min两个函数

1
2
3
4
5
6
7
8
9
   ncalls  tottime  percall  cumtime  percall filename:lineno(function)
625762426  319.980    0.000  319.980    0.000 circuit.py:286(__lt__)
   259964  315.431    0.001  635.431    0.002 circuit.py:381(_find_min)
    64400    1.371    0.000  639.636    0.010 circuit.py:423(step)
828793/634381    0.463    0.000    0.612    0.000 {built-in method builtins.len}
   194381    0.421    0.000  635.865    0.003 circuit.py:361(min)
    32768    0.352    0.000    0.352    0.000 {method 'write' of '_io.TextIOWrapper' objects}
    65554    0.309    0.000    0.723    0.000 circuit.py:163(transition_output)
        1    0.290    0.290  640.116  640.116 circuit.py:456(run)

随后题意要求基于原来的api实现一个优先队列(最小堆)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
class PriorityQueue:
    """Array-based priority queue implementation."""
    def __init__(self):
        """Initially empty priority queue."""
        self.queue = []
    def leftchid(self,key):
        return 2*key+1
    def rightchild(self,key):
        return 2*key+2
    def parent(self,key):
        return (key-1)//2
    def swap(self,key1,key2):
        temp=self.queue[key2]
        self.queue[key2]=self.queue[key1]
        self.queue[key1]=temp
    def __len__(self):
        # Number of elements in the queue.
        return len(self.queue)
    def sift_up(self,key):
        while True:
            p=self.parent(key)
            if (p<0 or self.queue[p]<=self.queue[key]):
                break
            else:
                self.swap(p,key)
                key=p
    def append(self, key):
        """Inserts an element in the priority queue."""
        if key is None:
            raise ValueError('Cannot insert None in the queue')
        self.queue.append(key)
        self.sift_up(self.__len__()-1)
    def min(self):
        """The smallest element in the queue."""
        if len(self.queue) == 0:
            return None
        return self.queue[0]
    def sift_down(self,key):
        while True:
            lft,rht = self.leftchid(key),self.rightchild(key)
            min_key=key
            if (lft<self.__len__() and self.queue[lft]<self.queue[key]):
                min_key=lft
            if (rht<self.__len__() and self.queue[rht]<self.queue[min_key]):
                min_key=rht
            if (min_key==key): break
            self.swap(min_key,key)
            key =min_key
    def pop(self):
        """Removes the minimum element in the queue.
        Returns:
            The value of the removed element.
        """
        if len(self.queue) == 0:
            return None
        self.swap(0,self.__len__()-1)
        min_val=self.queue.pop(self.__len__()-1)
        self.sift_down(0)
        return min_val
    def _find_min(self):
        # Computes the index of the minimum element in the queue.
        # This method may crash if called when the queue is empty.
        if self.__len__==0:
            raise ValueError('cannot find min of empty queue')
        return 0

python3可以运行所有测试，但无法运行可视化程序，不过也无所谓了，优化后再次运行一开始的输入

1
2
3
4
5
6
7
8
ncalls  tottime  percall  cumtime  percall filename:lineno(function)
    65583    2.826    0.000    5.321    0.000 circuit.py:389(sift_down)
    65583    1.006    0.000    1.901    0.000 circuit.py:366(sift_up)
  1930321    0.807    0.000    1.109    0.000 circuit.py:362(__len__)
  1349048    0.772    0.000    0.772    0.000 circuit.py:357(swap)
  1432334    0.719    0.000    0.719    0.000 circuit.py:286(__lt__)
    64400    0.698    0.000    9.608    0.000 circuit.py:451(step)
2450781/2256369    0.473    0.000    0.567    0.000 {built-in method builtins.len}

问题解决了,amdtel的offer什么时候发？