机器学习笔记 all in one

李宏毅机器学习 动手学深度学习

前期工作

数学

统计

机器学习的本质是寻找一个理想的函数,这个理想可以定义为在训练集和全集上表现几乎一致,使用统计的原理可以尽可能理解这其中的一些关系:
定义: |𝐿 ℎ, 𝒟𝑡𝑟𝑎𝑖𝑛 − 𝐿 ℎ, 𝒟𝑎𝑙𝑙 | > 𝜀时Dtrain是差的,那么:

\[P(\mathcal{D}_{t r a i n}\;i s\;b a d)\leq|\mathcal H|\cdot2e x p(-2N\varepsilon^{2})\]

其中,N是训练样本数,H为备选函数的集合,也就是如果想要这个理想条件,H和N会存在这种约束条件
需要注意的是,这个理想条件并不包括具体的loss值,如果H过小,那么loss就可能会很大

概率论

数学期望:

\[E[X]=\sum_{x}x P(X=x).\]

当函数f(x)的输入是从分布P中抽取的随机变量时,f(x)的期望值为:

\[E_{x\sim P}[f(x)]=\sum_{x}f(x)P(x).\]

方差：

\[\operatorname{Var}[X]=E\left[(X-E[X])^{2}\right]=E[X^{2}]-E[X]^{2}.\]

分布

信息论

熵

在不同的领域中，熵被表示为混乱程度，不确定性，惊奇程度，不可预测性，信息量等，但在机器学习中我们只需要对信息论中的熵有基本了解
信息论中熵的概念首次被香农提出，目的是寻找一种高效/无损地编码信息的方法，即无损编码事件信息的最小平均编码长度 即信息熵H(X) = -Σ p(x) log2 p(x) (p为概率)

接下来说明这个公式，假设我们用二进制的哈夫曼编码，一个信息出现概率是1/2,即其他所有情况加起来也是1/2，那么我们会发现其编码长度必然是-log(1/2),也就是1，恰好和我们的香农熵定义一致了，这是为什么呢？
严谨的数学证明超出了cs专业范围，这里只说一下直观理解，熵有两个性质：

• 概率越小信息量越大(如果一个小概率事件发生了，就排除了非常多其他可能性)
• 假设两个随机变量x,y相互独立，那么分别观测两个变量得到的信息量应该和同时观测两个变量的信息量是相同的，h(x+y)=h(x)+h(y)

如此一来对数函数的负数完美符合条件，基数则无所谓，直观地理解，基数对应用几进制编码，而要最短化编码，越小概率就应该用更长的位数，把短位数腾出来给大概率事件用，当然实际中编码的位数是离散的，而且相比对数取负只能多不能少，因此香农熵是一个理论最优值，熵编码就指无损情况下的编码方式，最常用的就是哈夫曼编码，所有熵编码方式的编码长度大于等于香农熵

现实中常用二进制编码信息，例如对8种不同的信息，最直观的编码是三位二进制，每三位表示一个独特信息。
我们可以用概率表示每种信息出现的可能，例如8种信息，每个都等可能出现，那么以概率为权的哈夫曼编码就会用所有的3位二进制编码这8种信息，熵就是3，而其他情况熵可以当做哈夫曼树的总编码长度算
那么如何理解熵能反映混乱度呢？如果熵比较大(即平均编码长度较长)，意味着这一信息有较多的可能状态，相应的每个状态的可能性比较低；因此每当来了一个新的信息，我们很难对其作出准确预测，即有着比较大的混乱程度/不确定性/不可预测性

交叉熵：
交叉熵用于评估估计概率得到的熵与真实熵的差距，交叉的含义很直观，就是使用P计算期望，使用Q计算编码长度
为什么这么选而不是反过来呢？这取决于我们的目的，一般来说，我们希望估计的编码长度和理论最优的熵差距较小，要比对取优的主要是模型的编码长度即logQ，可以这么理解，熵公式中的对数函数视为视为对一个特定概率事件的编码长度，由于现实的概率分布实际上是确定的，那么需要评估的也就是编码方式的效率
由于熵是给定概率分布下的最优值，交叉熵只可能大于等于熵，两者差越小或者说交叉熵越小表示模型估计越准
例如在最极端的one-hot编码中，交叉熵等价于对应正确解标签的输出的自然对数

线性代数

范数

范数是具有“长度”概念的函数，用于衡量一个矢量的大小（测量矢量的测度）
由于不是数学系的，这里就极为不严谨地记录一下范数的理解：

• 0范数，向量中非零元素的个数
• 1范数，为绝对值之和
• 2范数，就是通常意义上的模

正则化的目的可以理解为限制权重向量的复杂度，实际做法为在损失函数中加入与权重向量复杂度有关的惩罚项，而范数在某种意义上可以反映这点，因此可作为选取正则项的依据
顺便一提a star算法也会用类似的测度估计距离

工具

cuda

Compute Unified Device Architecture (CUDA):简单地说，就是允许软件调用gpu来计算的一个接口
CUDA Runtime API vs. CUDA Driver API

• 驱动版本需要≥运行时api版本
• driver user-space modules需要和driver kernel modules版本一致
• 当我们谈论cuda时，往往是说runtime api

以下是nvida的介绍原文：

It is composed of two APIs:

• A low-level API called the CUDA driver API,
• A higher-level API called the CUDA runtime API that is implemented on top of the CUDA driver API.

The CUDA runtime eases device code management by providing implicit initialization, context management, and module management. The C host code generated by nvcc is based on the CUDA runtime (see Section 4.2.5), so applications that link to this code must use the CUDA runtime API.

In contrast, the CUDA driver API requires more code, is harder to program and debug, but offers a better level of control and is language-independent since it only deals with cubin objects (see Section 4.2.5). In particular, it is more difficult to configure and launch kernels using the CUDA driver API, since the execution configuration and kernel parameters must be specified with explicit function calls instead of the execution configuration syntax described in Section 4.2.3. Also, device emulation (see Section 4.5.2.9) does not work with the CUDA driver API.

简单地说,driver更底层，更抽象但性能和自由度更好，runtime则相反

容器

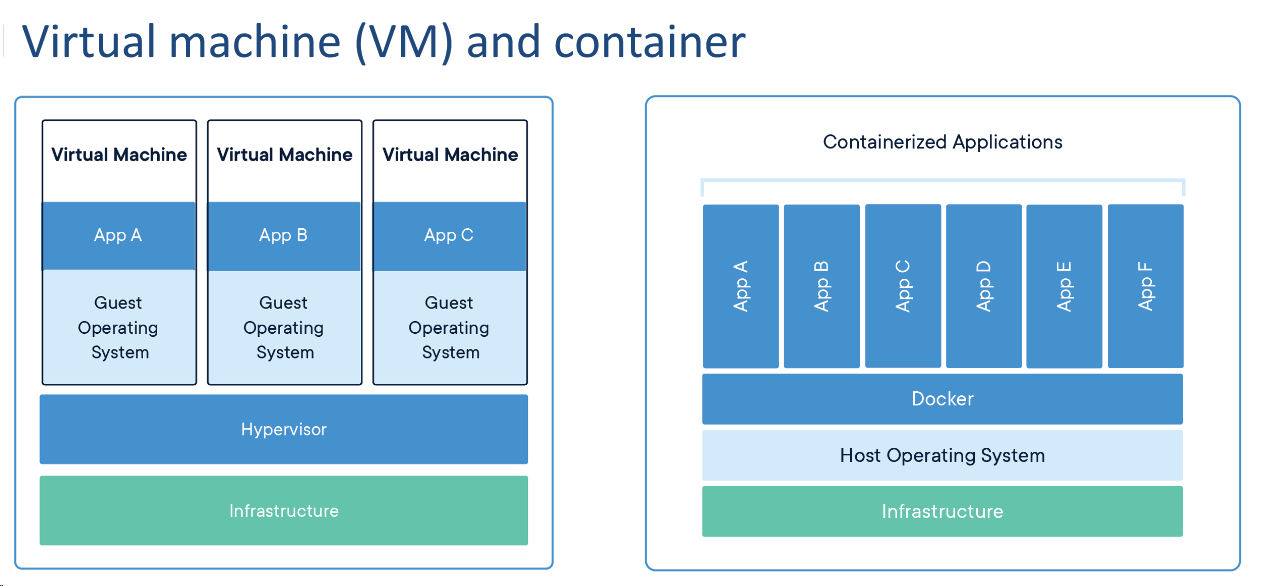
infrastructure(基础设施)
简单地说，虚拟机的隔离级别比容器更高，虚拟机会模拟出一个系统及其系统api，而docker依旧调用宿主机的api，因此docker更为轻量级
docker是处理复杂环境问题的良策，比虚拟机更为轻量
其他常用的容器:Slurm and Kubernetes

Docker Hub repository of PyTorch

python

import numpy as np 
import matplotlib.pyplot as plt  
# 生成数据  x = np.arange(0, 6, 0.1) # 以 0.1 为单位,生成 0 到 6 的数据 

y1 = np.sin(x)
y2 = np.cos(x)  

# 绘制图形  
plt.plot(x, y1, label="sin") plt.plot(x, y2, linestyle = "--", label="cos") 
# 用虚线绘制 
plt.xlabel("x") 
# x 轴标签 
plt.ylabel("y") 
# y 轴标签 
plt.title('sin & cos') 

plt.show()

理论

官方文档
Official Pytorch Tutorials
pytorch-for-numpy-users

张量

张量tensor:用于表示n维数据的一种概念，例如一维张量是向量，二维是矩阵……

dim in PyTorch == axis in NumPy

import torch
import numpy as np

def test():
    print("", torch.cuda.is_available())
    if torch.cuda.is_available():
        device = torch.device("cuda")
        print(f"There are {torch.cuda.device_count()} GPU(s) available.")
        print("Device name:", torch.cuda.get_device_name(0))
    else:
        print("No GPU available, using the CPU instead.")
        device = torch.device("cpu")
test()

 True
There are 1 GPU(s) available.
Device name: NVIDIA GeForce RTX 2070

以下是一些朴素的张量操作:

x = torch.tensor([[1, -1], [-1, 1]])
print(x)
x = torch.from_numpy(np.array([[1, -1], [-1, 1]]))
print(x)

tensor([[ 1, -1],
        [-1,  1]])
tensor([[ 1, -1],
        [-1,  1]])

x = torch.zeros([2, 2])
print(x)
x = torch.ones([1, 2, 5]) 
print(x)

tensor([[0., 0.],
        [0., 0.]])
tensor([[[1., 1., 1., 1., 1.],
         [1., 1., 1., 1., 1.]]])

x = torch.zeros([2, 3])
print(x.shape)

x = x.transpose(0, 1)
print(x.shape)

torch.Size([2, 3])  
torch.Size([3, 2])

A = torch.arange(20, dtype=torch.float32).reshape(5, 4) 
B = A.clone() # 通过分配新内存,将A的一个副本分配给B  

A*B#按元素乘法的Hadamard积，即矩阵相同位置的元素相乘，得到结果矩阵该位置的元素，数学符号⊙

'''
结果如下：
tensor([[ 0., 1., 4., 9.], 
        [ 16., 25., 36., 49.], 
        [ 64., 81., 100., 121.],
        [144., 169., 196., 225.],
        [256., 289., 324., 361.]])

'''

A_sum_axis0 = A.sum(axis=0)  #沿0轴对A求和
A_sum_axis0, A_sum_axis0.shape


'''
numpy的对某一轴求和，就是把输入轴所有值加起来，投影到剩下的轴上，这个轴不是消失了，而是现在被投影到一起，例如二维矩阵里，沿0轴求和，就是沿着所有行求和，所有行的对应元素加起来，投影到一行，结果行数为1可以降低一个维度为向量，作为sum的输出(更高维情况下除了输入轴都不变，最后维度-1)
在这个例子中，结果是：
(tensor([40., 45., 50., 55.]), torch.Size([4]))

如果让sum的参数keepdims=True，就不会执行维度减一的操作，结果会是个行数1，列数4的矩阵

'''

沿某个轴计算A元素的累积总和,比如axis=0(按行计算),可以调用cumsum函数。此函数不会沿任何轴降低输入张量的维度。

A.cumsum(axis=0)  
tensor([[ 0., 1., 2., 3.],  
        [ 4., 6., 8., 10.],  
        [12., 15., 18., 21.],  
        [24., 28., 32., 36.],  
        [40., 45., 50., 55.]])

神经网络的定义

对每一层神经网络，输入的x乘以权重向量w(eight)，加上一个标量b(ias)后就是输出y
例如训练一个将32维向量转化为64维向量输出的模型，权值矩阵规模是64×32,输入向量是32×1，输出是64×1
算出线性的权值和之后，增加一层激活函数Activation Function,激活函数常是非线性的，用于增强网络学习能力，如果没有激活函数，网络就是单纯的有很多层数的线性回归
最基础的神经网络是全连接前馈神经网络(fully-connected feed-forward network):前馈表示从前到后训练，全连接表示相邻的两层中，所有的神经元都是相连的;网络第一层称为输入层（input layer），最后一层称为输出层（output layer），中间的层数被称为隐藏层(hidden layer)

前向和反向，forward && backward:理解这两个词应该看英文，forward这个前指的是时间上从前往后，也就是训练时的正常时间顺序，backward与其相反，就是从结果推开头

深度学习：这个定义非常简单粗暴，意思是隐藏层很多，一般可能有三位数起步，并非越多层就越好，这需要合适的数据集，合适的提取特征方式，即特征工程feature engineering，才能定义一个较好的网络

常见激活函数：

• Sigmoid函数也叫Logistic函数，用于隐层神经元输出，取值范围为(0,1)，它可以将一个实数映射到(0,1)的区间，可以用来做二分类。在特征相差比较复杂或是相差不是特别大时效果比较好，图像类似一个S形曲线:
  • $ f(x)=\frac{1}{1+e^{-x}} $
• ReLU函数又称为修正线性单元（Rectified Linear Unit），是一种分段线性函数，弥补了sigmoid函数的梯度消失问题(即该函数两端非常平滑，导数趋近0，遇到数值偏两端的数据，loss很难传播):
  • $f(x)={\left\{\begin{array}{l l}{x}&{,x\gt =0}\\ {0}&{,x\lt 0}\end{array}\right.} $

损失函数loss function：评估训练成果的一个标准，越小越好
loss = criterion(model_output, expected_value) #nn:neural network

• criterion = nn.MSELoss():Mean Squared Error
• criterion = nn.CrossEntropyLoss():Cross Entropy 交叉熵

常见问题

1. 模型偏差：模型在训练资料上的损失函数很大时，可能是因为在这个问题中选择的模型太过简单，以至于无论用这个给模型选择什么样的参数θ，损失函数f(θ)都不会变得很小
2. 优化问题，梯度下降看上去很美好，但常常会卡在一个局部最优（local minima）点，这个局部最优可能和全局最优（global minima）差得很远，因此需要选取更好的优化算法如 Adam，RMSProp，AdaGrad 等
3. 过拟合，训练集Loss很小，测试集却很大，需要注意的是首先得满足前一个条件，不然也可能是1.2.问题
   1. 最有效的一种解决方案是增加训练资料，但很多时候是无法做到的
   2. 第二种方法就是数据增广（Data Augmentation），常用于图像处理。既然不能增加数据，那就更好地利用现有数据；例如：对图像左右镜像，改变比例等等，需要注意不能过度改变数据特征，例如上下颠倒图片
   3. 增加对模型的限制，常见如早停止，正则化，丢弃部分不合理数据等等

优化算法 optimizer

torch.optim
e.g.

1. optimizer.zero_grad()：重设梯度(即训练完一段后梯度置0,截断反向传播再继续训练)
2. Call loss.backward() 反向传播以减少损失
3. Call optimizer.step() 调整模型参数

归一化 Normalization

训练中的数据很多情况下大小完全不统一，基于直觉的想法是：同一维度的数据我们只关心其相对大小关系，不同维度的数据我们认为它们的地位平等，尺度应到一致，所以需要归一化
简单地说就是把一个维度的数据大小都调整到[0-1]这个区间，例如softmax函数就用于将一个向量转化成概率分布(令其总和为1)

归一化normalization容易和正则化regularization搞混，来看看词典解释：

• normalization: to start to consider something as normal, or to make something start to be considered as normal
• regularization: the act of changing a situation or system so that it follows laws or rules, or is based on reason

也就是，归一化偏向于“正常”，正则化偏向于“规则”，差别非常微妙，但硬要说的话，0-1的数据看起来是比其他的更“正常”一点

神经网络中进行的处理有推理(inference)和学习两个阶段。神经网络中未被正规 化(归一化)的输出结果有时被称为“得分”。也就是说,当神经网络的推理只需要给出一个答案的情况下,因为此时只对得分最大值感兴趣,所以不需要 Softmax 层。 不过,神经网络的学习阶段则需要 Softmax 层

梯度下降

梯度下降法：
有点类似于牛顿法(牛顿法理论是二阶收敛，梯度则为一阶，牛顿法速度更快计算量更大)，所谓的梯度就是一个多元函数中，对一个点求各个元的偏导数取值组成的一个表示方向的向量(即偏导数乘对应元的单位向量)
这个梯度一般指向当前点增加最快的方向，把他乘以-1就会得到下降最快的方向(一般用于最小化损失函数)，梯度只表示方向，因此还需要选择合适的步长α，乘以方向向量后就得到移动的路径，步长太长了会跨过极小值然后来回震荡，太短了效率会很差
梯度下降算法需要设置一个学习率(learning rate)，每次迭代中，未知参数的梯度下降的步长取决于学习率的设置，这种由人为设定的参数被称为超参（hyperparameters）
如果我们的数据集很大，计算梯度会相当复杂，则可以分为n个batch,每个batch有B个资料，即 mini-batch 梯度下降（MBGD，Mini-Batch GradientDescent
在numpy里用形如np.random.choice(scope, num)的方法就可以在scope内随机选取num个索引作为mini batch

反向传播

通俗讲解反向传播
反向传播是梯度下降在神经网络上的具体实现方式，与前向训练过程相反，用结果的损失值修正训练中的权值，在数学上就是求损失对前一层权重的偏导数
但是损失函数的参数是本层的输出值，因此需要链式法则求偏导，先求出损失函数对输出的偏导，再乘以本层输出对前一层权重的偏导(当然我们知道本层神经元收到上层的输出后还要算个激活函数才能得到最后的输出，因此中间还有一步本层输出对上层输出求偏导，只有上层输出直接和上层权重有关)

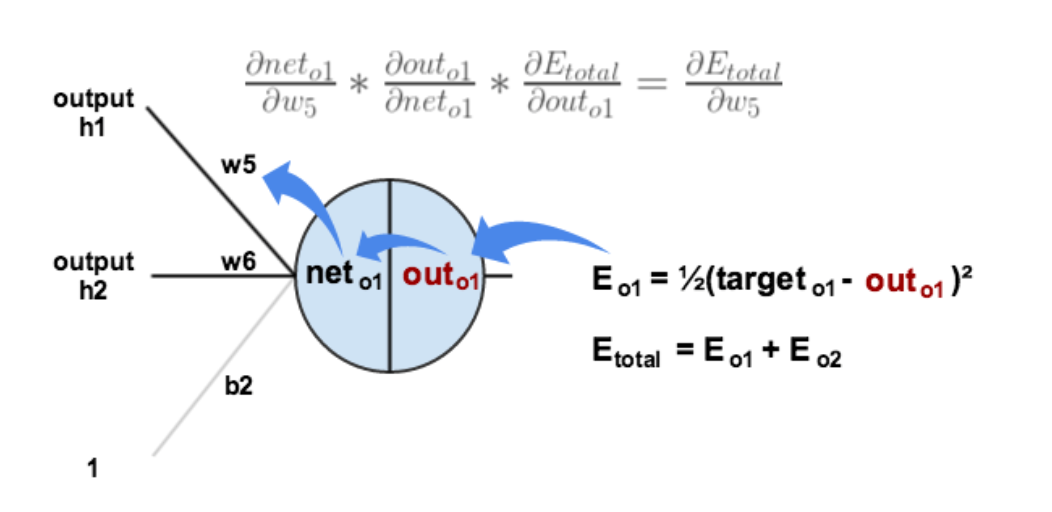如图，权重结合上层out得到net,net经过激活函数得到本层out，本层out用来计算损失值，因此反向传播会反过来算
对着这些复杂的名称求偏导数看起来有点奇怪，但这和常见的yx没什么不同
得到偏导函数后，接下来正如在梯度下降中学到的，我们希望通过不断调整上层权重来最小化结果层的损失函数，每次用一个“学习速率 \(\eta\) ”乘以偏导数来更新权重

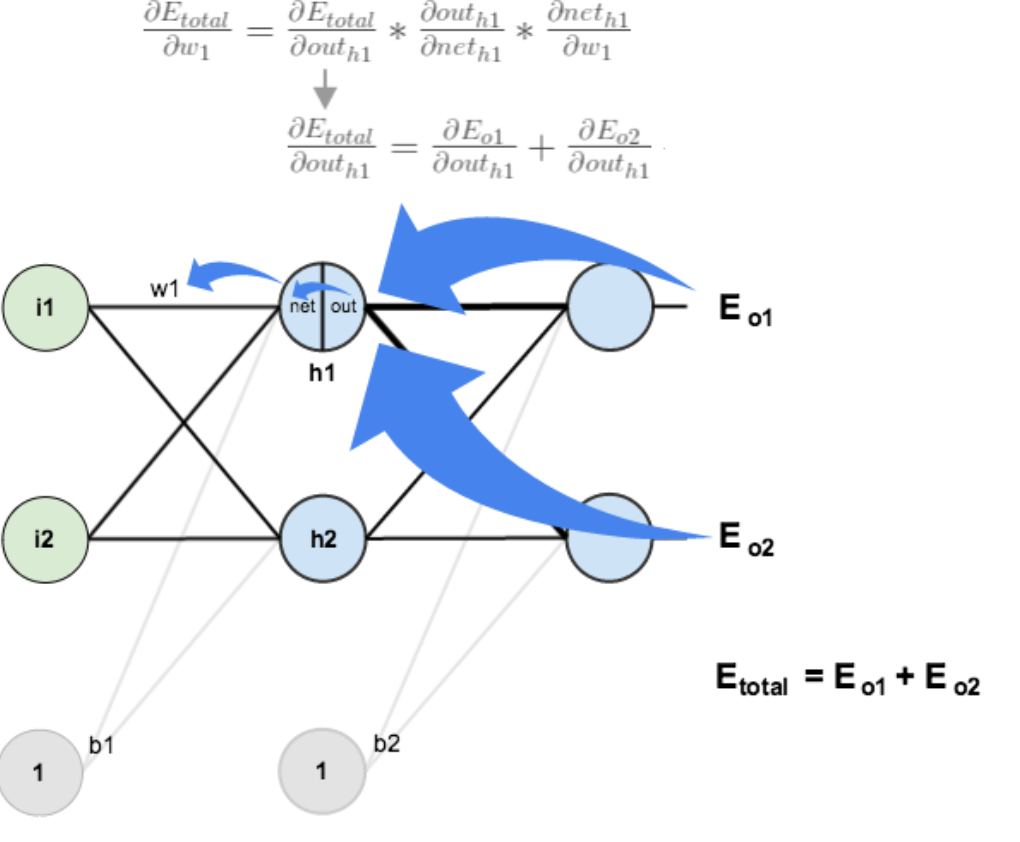
涉及隐藏层时稍微有所不同，在由于隐藏层的下一层会连到不同的结果，也就会产生多个损失值，在out部分需要对不同的损失值求偏导，即总误差对outh1的偏导是E(o1)和E(o2)对outh1偏导的和

dataset = MyDataset(file)
tr_set = DataLoader(dataset, 16, shuffle=True)
model = MyModel().to(device)
criterion = nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), 0.1)

for epoch in range(n_epochs):
    model.train()
    for x, y in tr_set:
        optimizer.zero_grad()
        x, y = x.to(device), y.to(device)
        pred = model(x)
        loss = criterion(pred, y)
        loss.backward()
        optimizer.step() #更新模型的参数

梯度消失：

如果我们用最常见的sigmoid函数，且在某层上输入值在函数的两端，此时导数非常小，也就是梯度非常小，这层上的反向传播几乎无法更新，不仅如此，更之前的层级也很难继续传播，这就是所谓的梯度消失问题。
除了更新缓慢问题外，这还会导致浅层和深层的更新程度区别巨大，让模型变得“不均匀”，此外，由于sig函数的梯度区间较小，模型深了几乎必然有这种问题

ReLU用于解决梯度消失问题，其梯度要么是0要么是1，只在负端消失，这样有个可能的好处，如果负端的数据其实是噪声或者是一些我们不关注的特征，那么扔掉反而会让模型效果更好
这种激活函数的缺点是，梯度非负数，对于一层所有的w，梯度的符号都是一样的，只能一起增大或者减小，这可能减少模型的准确度
通常，激活函数的输入值有一项偏置项(bias)，假设bias变得太小，以至于输入激活函数的值总是负的，那么反向传播过程经过该处的梯度恒为0,对应的权重和偏置参数此次无法得到更新。如果对于所有的样本输入，该激活函数的输入都是负的，那么该神经元再也无法学习，称为神经元”死亡“问题

LeakyReLU的提出就是为了解决神经元”死亡“问题，其输入小于0的部分，值为负，且有微小的梯度，除了避免死亡还有一个可能的好处是，该微小的梯度可能让训练有一些微小的振动，在特定情况能跳出局部最优解

python实现:

def sigmoid(x): 
    return 1 / (1 + np.exp(-x)) #NumPy的广播特性:如果在标量和 NumPy 数组之间进行运算,则标量会和 NumPy 数组的各个元素进行运算

def relu(x): 
    return np.maximum(0, x)

参考项目:

• Huggingface Transformers (transformer models: BERT, GPT, ...)
• Fairse (sequence modeling for NLP & speech)
• ESPnet (speech recognition, translation, synthesis, ...)

Momentum

梯度下降简单易懂，但当然也存在问题，考虑如下的函数：

\[f(x,y)=\frac{1}{20}x^{2}+y^{2}\]

其x轴梯度远小于y轴梯度，函数像一个山岭，但底部是个起伏不大的抛物线，更新路径是一个个之字形，y轴更新地快不断震荡，x轴则慢慢向真正的底部前进
也就是说，对非均向(anisotropic)的函数，梯度下降效率有限

Momentum(动量)是一种改进的优化方式，这里不管其物理含义，具体更新方法如下所示：

\[v\leftarrow\alpha v-\eta{\frac{\partial L}{\partial W}}\] \[W\leftarrow W+v\]

其他变量我们都知道了，这个v对应物理上的速度，表示物体在梯度方向受力，α模拟类似摩擦力导致的减速，一般比1略小，如0.9，也就是说，原来的梯度下降可视为无阻力的运动，动量法让其速度越来越慢，这可以有效减少路径的折线情况

AdaGrad

学习率衰减(learning rate decay),即随着学习的进行,使学习率逐渐减小是一种常见的思路；AdaGrad进一步发展了这个想法,针对不同参数,赋予相互独立的学习率，即Adaptive Grad

\[h\leftarrow h+{\frac{\partial L}{\partial W}}\leftarrow{\frac{\partial L}{\partial W}}\] \[W\leftarrow W-\eta\frac{1}{\sqrt{h}}\frac{\partial L}{\partial W}\]

h保存了以前的所有梯度值的平方和,这样能够按参数的元素进行学习率衰减,使变动大的参数的学习率逐渐减小，直至无限接近0；RMSProp 方法会舍弃一些比较早的梯度避免这个问题
为了避免棘手的除0问题，h的平方根可以加一个微小值如1e-7

adam是2015年提出的新方法,直观但不准确地说就是融合了 Momentum 和 AdaGrad 的方法

正则化

正则化指为解决适定性问题或过拟合而加入额外信息的过程，在机器学习中，常见的就是为损失函数添加一些调整项
根据前文所述，学习的过程就是根据损失函数与权重的关系不断调整权重以最小化损失，而正则化的目的是不要让权重关系太复杂以致于没有普适性。我们将原始的损失函数画一个图，正则项再画一个图，需要找的就是两个函数同样权重基础上的最小和
用比较简单的双权重，均方误差损失函数来说，w1,w2就是xy轴，最后的loss作为z轴，原始损失函数L可能千奇百怪，但最后要找的是其与正则项的最小和.这个值通常在两个函数的交点取，而(二维层面上)L1的图像是菱形，l2是个圆，符合直观地推导，前者交点很容易在坐标轴上取，后者容易在离坐标轴近的地方取，即l1容易让权重稀疏，L2容易让它们的值的绝对值较小且分布均匀
数学上讲，抛开不确定的损失函数，l1正则项的导数是w×正负信号量，迭代时如果w大于0会减少，大于0会增加，最后很容易变成0；而l2的导数是w的一次函数且一次项系数小于1，迭代让w不断减小，这个减小量与w本身有关，因此一般来说不容易减到0

训练技巧

初始权值

什么是最好的初始权重？这个问题很难回答，不如反过来举一些反例
相同的权重肯定是最坏的选择，由于随机梯度下降法对相同或者相似的权值会有非常相似的传导效果，最终模型的权值也会趋同，降低其表达力

一般来说，我们用高斯分布来初始权重，例如常用的Xavier初始值根据上层(以及下层)的节点数量确定初始权重的分布，例如在与前一层有n个节点连接时,初始值使用标准差为 \(\frac{1}{\sqrt{n}}\) 的分布
Xavier初始值是以激活函数是线性函数为前提而推导出来的。因为sigmoid函数和tanh函数左右对称,且中央附近可以视作线性函数,所以适合使用Xavier初始值。但当激活函数使用ReLU时,一般推荐使用ReLU专用的初始值,也就是Kaiming He等人推荐的初始值,也称为“He初始值”
当前一层的节点数为n时,He初始值使用标准差为 \(\sqrt{\frac{2}{n}}\) 的高斯分布。当Xavier初始值是 \({\sqrt{\frac{1}{n}}}\) 时,(直观上)可以解释为,因为ReLU的负值区域的值为0,为了使它更有广度,所以需要2倍的系数

Batch Normalization

Batch Norm的思路是调整各层的激活值分布使其拥有适当的广度,具体而言,就是进行使数据分布的均值为0、方差为1的正规化

\[\mu_{B}\,\leftarrow\,\frac{1}{m}\sum_{i=1}^{m}x_{i}\] \[\sigma_{B}^{2}\iff\sum_{i=1}^{m}(x_{i}-\mu_{B})^{2}\] \[\hat{x}_{i}\enspace\leftarrow\ \frac{x_{i}\leftarrow\mu_{B}}{\sqrt{\sigma_{B}^{2}\,+\,\varepsilon}}\,\]

ε 是一个微小值，用来防止除0

Batch Norm 层会对正规化后的数据进行缩放和平移的变换:

\[y i\longleftarrow\gamma\hat{x}_{i}+\beta\]

γ、β是参数，初始为1、0，随后根据学习来调整

抑制过拟合

权值衰减：为损失函数加上权重的平方范数(L2范数)，即让正则项为 \(\textstyle{ {\frac{1}{2}}\lambda W^{2} }\) ，其中λ是控制正则化强度的超参数，其梯度也会加上一个λW

dropout：在学习的过程中随机删除神经元，停止向前传递信号

class Dropout:
    def __init__(self, dropout_ratio=0.5):
        self.dropout_ratio = dropout_ratio
        self.mask = None

    def forward(self, x, train_flg=True):
        if train_flg:
            self.mask = np.random.rand(*x.shape) > self.dropout_ratio#*x.shape 将 x 的形状解包
            return x * self.mask
        else:
            return x * (1.0 - self.dropout_ratio)

    def backward(self, dout):
        return dout * self.mask

集成学习：让多个模型单独进行学习,推理时再取多个模型的输出的平均值。Dropout可以理解为：通过在学习过程中随机删除神经元,从而每一次都让不同的模型进行学习；推理时,通过对神经元的输出乘以删除比例,可以取得模型的平均值。

超参数

超参数(hyper-parameter)：如各层的神经元数量、batch 大小、参 数更新时的学习率或权值衰减等
需要注意的是，不能使用测试数据评估超参数的性能，否则会让超参数的值会对测试数据发生过拟合，一般用验证数据来评估性能 有报告显示，在进行神经网络的超参数的最优化时,与网格搜索等有规律的搜索相比,随机采样的搜索方式效果更好。这是因为在 多个超参数中,各个超参数对最终的识别精度的影响程度不同 大致的步骤是：

1. 设定超参数的范围
2. 从设定的超参数范围中随机采样
3. 使用1.中采样到的超参数的值进行学习,通过验证数据评估识别精度(但是要将epoch设置得很小)
4. 重复1. 2. 不断缩小参数到一个合理的值

weight_decay = 10 ** np.random.uniform(-8, -4)#uniform生成指定范围内的随机数,默认0维度，可以指定维度

神经网络模型

python 相关

• DataLoader(train_date,shuffle=True)中shuffle表示打乱数据集，符合直觉的想法是：这对避免过拟合有帮助
  
• epoch是一个单位。一个epoch表示学习中所有训练数据均被使用过一次时的更新次数。比如,对于 10000 笔训练数据,用大小为100笔数据的mini-batch进行学习时,重复随机梯度下降法100次,所有的训练数据就都被“看过”了。此时,100次就是一个epoch

class My_model(nn.Module):
    def __init__(self，inputdim):
        super(My_model,self).__init__()
        self.layers=nn.sequential(#将多个层按顺序组合在一起
            nn.Linear(input_dim,64), 
            nn.ReLU(),
            nn.Linear(64，32),
            nn.ReLU(),
            nn.Linear(32，1)
        )

    def forward(self, x):
        x = self.layers(x)
        x = x.sgueeze(1)#(B,l) -> B
        return x

#Training loop
for epoch in range(3000):
    model.train() # Set your model to train mode.
    # tgdm is a package to visualize your training progress
    train_pbar = tqdm(train_loader, position=0, leave=True)
    for x, y in train_pbar:
        x, y = x.to('cuda'), y.to('cuda')
        pred = model(x)
        loss = criterion(pred, y)
        loss.backward()# Compute gradient(backpropagation).
        optimizer.step()# Update parameters.
        optimizer.zero_grad() # Set gradient to zero.

PyTorch Documentation

广播机制(broadcasting mechanism):

1. 通过适当复制元素来扩展一个或两个数组,以便操作的不同张量具有相同的形状;
   
2. 对生成的数组执行按元素操作

例如，a和b分别是3 × 1和1 × 2矩阵，广播会成为一个更大的3 × 2矩阵:矩阵a将复制列,矩阵b将复制行,然后再按元素相加 广播机制有一些实用的技巧:

A = torch.arange(20, dtype=torch.float32).reshape(5, 4) 
sum_A = A.sum(axis=1, keepdims=True)

A / sum_A #sum_A没有降维，仍然是个矩阵，可以通过广播将A除以sum_A。

'''
结果如下：
tensor([[0.0000, 0.1667, 0.3333, 0.5000],  
        [0.1818, 0.2273, 0.2727, 0.3182],
        [0.2105, 0.2368, 0.2632, 0.2895],  
        [0.2222, 0.2407, 0.2593, 0.2778],  
        [0.2286, 0.2429, 0.2571, 0.2714]])

这是一种很方便的归一化操作
'''

基础训练方法示例

def load_array(data_arrays, batch_size, is_train=True):  #@save
    """构造一个PyTorch数据迭代器"""
    dataset = data.TensorDataset(*data_arrays)
    return data.DataLoader(dataset, batch_size, shuffle=is_train)

batch_size = 10
data_iter = load_array((features, labels), batch_size)

使用iter构造Python迭代器，并使用next从迭代器中获取第一项

next(iter(data_iter))

[tensor([[-0.0714, -1.8597],
         [-0.4744,  0.4050],
         [ 0.2402,  0.5660],
         [ 1.6367, -0.9899],
         [ 0.6723,  0.1904],
         [ 0.5322, -0.4337],
         [-0.5749,  0.6719],
         [-0.0317,  1.3456],
         [ 1.0865, -1.3968],
         [-0.0130, -0.9245]]),
 tensor([[10.3747],
         [ 1.8749],
         [ 2.7762],
         [10.8325],
         [ 4.9005],
         [ 6.7224],
         [ 0.7743],
         [-0.4169],
         [11.1058],
         [ 7.3157]])]

Sequential类将多个层串联在一起,并自动让其前向传播
在PyTorch中，全连接层在Linear类中定义。
值得注意的是，我们将两个参数传递到nn.Linear中，第一个指定输入特征形状，即2，第二个指定输出特征形状，输出特征形状为单个标量，因此为1。

# nn是神经网络的缩写
from torch import nn

net = nn.Sequential(nn.Linear(2, 1))

可以直接访问参数以设定它们的初始值，如通过net[0]选择网络中的第一个图层，然后使用weight.data和bias.data方法访问参数。
我们还可以使用替换方法normal_和fill_来重写参数值。

net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)

损失函数与优化算法：

loss = nn.MSELoss()
trainer = torch.optim.SGD(net.parameters(), lr=0.03)#使用小批量随机梯度下降，第一个参数是优化对象，lr则是学习率

训练：

num_epochs = 3
for epoch in range(num_epochs):
    for X, y in data_iter:
        l = loss(net(X) ,y)
        trainer.zero_grad()
        l.backward()
        trainer.step()
    l = loss(net(features), labels)
    print(f'epoch {epoch + 1}, loss {l:f}')

epoch 1, loss 0.000247
epoch 2, loss 0.000110
epoch 3, loss 0.000110

比较生成数据集的真实参数和通过有限数据训练获得的模型参数
要访问参数，我们首先从net访问所需的层，然后读取该层的权重和偏置

w = net[0].weight.data
print('w的估计误差：', true_w - w.reshape(true_w.shape))
b = net[0].bias.data
print('b的估计误差：', true_b - b)

w的估计误差： tensor([0.0005, 0.0006])
b的估计误差： tensor([0.0006])

线性模型

回归问题常常用若干输入产生一个连续值作为输出，线性回归（Linear Regression）和逻辑回归（Logistics Regression）是常见的线性模型

线性回归

线性回归，即y = wx + b ,是最简单的回归模型，但纯一次项的拟合能力较为受限，这种情况下就需要多项式回归
我们将w视为权值向量，x视为从一次x'到n次x'组成的向量，那么多项式模型依旧可以用原先的线性公式表示
增加多项式的次数可以更好拟合训练集，但对测试集的效果就未必了，很容易出现过拟合问题,如果出现，依旧需要正则化，增加数据数量或者维度等优化 线性模型优化是个纯粹的数学问题，其解析解在线代课上就会讲到，即：

\[\mathbf{w}^{*}=(\mathbf{X}^{\mathsf{T}}\mathbf{X})^{-1}\mathbf{X}^{\mathsf{T}}\mathbf{y}.\]

python实现

求梯度更像一个数学问题，这里就用pytorch的自动求导功能，实际上也可以自己通过计算图实现
简单生成一个有噪声项 \(\epsilon\) 的数据集，噪声项有标准差0.01,均值为0的正态分布生成

def synthetic_data(w, b, num_examples):  #@save
    """生成y=Xw+b+噪声"""
    X = torch.normal(0, 1, (num_examples, len(w)))根据正态分布随机计算初始权值向量
    y = torch.matmul(X, w) + b
    y += torch.normal(0, 0.01, y.shape)
    return X, y.reshape(-1,1)#-1表示不固定形状，根据总元素数和其他维度数量计算该维度

true_w = torch.tensor([2, -3.4])#w形状与features单行的形状相同
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)#labels被reshape为单列的向量
labels.shape

torch.Size([1000])

通过生成第二个特征features[:, 1]和labels的散点图， 可以直观观察到两者之间的线性关系。

d2l.set_figsize()#控制图像大小
d2l.plt.scatter(features[:, 1].detach().numpy(), labels.detach().numpy(), 1);#detach() 用于从计算图中分离张量

svg

为了提高效率，设置一个划分小批量的工具函数：

def data_iter(batch_size, features, labels):
    num_examples = len(features)
    indices = list(range(num_examples))
    # 这些样本是随机读取的，没有特定的顺序
    random.shuffle(indices)
    for i in range(0, num_examples, batch_size):
        batch_indices = torch.tensor(
            indices[i: min(i + batch_size, num_examples)])
        yield features[batch_indices], labels[batch_indices]

定义模型：

def linreg(X, w, b): 
    """线性回归模型"""
    return torch.matmul(X, w) + b

def squared_loss(y_hat, y): 
    """均方损失"""
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2

def sgd(params, lr, batch_size):  
    """小批量随机梯度下降"""
    with torch.no_grad():
        for param in params:
            param -= lr * param.grad / batch_size
            param.grad.zero_()

w = torch.normal(0, 0.01, size=(2,1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss

for epoch in range(num_epochs):    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w, b), y)  # X和y的小批量损失
        # 因为l形状是(batch_size,1)，而不是一个标量。l中的所有元素被加到一起， 并以此计算关于[w,b]的梯度
        l.sum().backward()
        sgd([w, b], lr, batch_size)  # 使用参数的梯度更新参数
    with torch.no_grad():
        train_l = loss(net(features, w, b), labels)
        print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')

epoch 1, loss 0.030660
epoch 2, loss 0.000105
epoch 3, loss 0.000046

print(f'w的估计误差: {true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差: {true_b - b}')

w的估计误差: tensor([ 0.0001, -0.0006], grad_fn=<SubBackward0>)
b的估计误差: tensor([0.0004], grad_fn=<RsubBackward1>)

分类

分类问题最简单的解决方法莫过于对回归产生的结果进行筛选，一个区间对应一个类别，但这么做会很难处理区间的划分情况，因此需要其他的处理方法
分类问题的损失函数与回归不同，可以单纯用分类错误率计算，常用模型有感知机、支持向量机等

感知机

感知机接收多个输入信号,根据权重输出一个信号，例如0和1
如果我们用最简单的感知机(依旧输出一个连续值，通过激活函数产生分类)，那么分类任务的重点就是找的一个合适的门槛值threshold
需要注意的是，感知机本质上是个线性的界限，通过权重向量和偏置值划分不同的输入，设想这样的情况：

1. 有多种输入需要分成两类
2. 其中一类有两个输入连成直线L1,另一类中有两个输入可以连成直线L2
3. 如果L1和L2相交，那么我们不可能在中间画一条线把两个直线分开(证明就不管了)

事实上，例如异或门就无法通过感知机实现，因为我们要分开(1,0)(0,1)以及(0,0)(1,1)，这两类的连线相交，准确地说，这是说单层感知机，因为曲线就可以划分这两类，也就是“单层感知机无法分离非线性空间”
例如，对异或门这个问题。加一层神经就能将分界线拓展为抛物线，也就是次数+1，这样就能进行非线性划分(多层感知机) 此外，也可以通过加一层feature转化层，将原来的x映射为可以被线性划分的x'

python中定义阶跃函数(输入超过阈值,就切换输出):

def step_function(x): 
    y=x>0 return #产生bool数组
    y.astype(np.int) # 将bool数组转换为1与0的int数组

def step_function(x): 
    return np.array(x > 0, dtype=np.int) 

x = np.arange(-5.0, 5.0, 0.1) 
y = step_function(x) 
plt.plot(x, y) 
plt.ylim(-0.1, 1.1) # 指定 y 轴的范围 
plt.show()

逻辑回归(discriminative model)

逻辑回归的目标是预测一个二元变量（例如，0或1、是或否）。通过逻辑函数（sigmoid 函数）将线性组合的输入转换为概率值
相比线性回归，其最大的特点是输出在0-1之间，可以理解为概率，一般用于处理分类（二分）问题

经过简单（并不）的梯度运算，可以得到常用loss函数的梯度为：

1. 交叉熵: \(\sum_{n}-{\bigg(}{ {\hat{y}^{n}-f_{w,b}(x^{n})} { } } {\bigg)}x_{i}^{n}\)
2. 均方根: \(2(f_{w,b}(x)-\hat{y})f_{w,b}(x)\left(1-f_{w,b}(x)\right)x_{i}\)

这样一来就有个问题，均方根的梯度在损失较大和较小时都很小，只有交叉熵符合远更新快近更新慢的条件

基于概率的分类方法(generative model)

如果有两个类c1,c2用于分类，抽到一个样本x,这就像高中数学地抽小球问题，随机抽个样本是某类小球的概率取决于在抽取的黑盒子里不同类别的分布。
此时我们的目的是根据参数预测分类，也就是说不同类别的分布只能猜想，于是假设在最简单的两个参数情况下，概率密度函数满足基于这两个参数的高斯(正态)分布，训练时，我们希望分别通过样本得到两类各自的分布情况，也就是这个高斯分布的均值和协方差矩阵

极大似然估计可以理解为利用已知的样本结果信息，反推最具有可能（最大概率）导致这些样本结果出现的模型参数值，例如抽球(放回式)问题中抽一百次，七十次是白球,三十次为黑球，若抽到白球的概率是p，这个结果的概率是p^70(1-p)30，符合直觉的猜想是p=0.7，这是因为我们下意识用了极大似然估计。
要令出现此情况的概率最大，只需要求导算一次极值就会得到p=0.7，由此产生了一个估计

使用极大似然估计，类似抽球问题，得到目前结果的概率其实结果所有取样点概率的积，省略怎么计算，最后我们能得到两组(μ, ∑)
此时模型确定了，我们可以得到P(x|Ci), i = 1, 2，这是种先验概率（Prior Probability），通过贝叶斯公式就能算出后验概率（Posterior Probability）：P(Ci|x)

\[ P(A | B) = \frac{P(B | A) \cdot P(A)}{P(B)} \]

这么一来，分类就可以根据最大后验概率对应的种类来选
优化：
为了避免过拟合可以统一∑，模型概率变为： \[\operatorname{L}(u^{1},\vert u^{2},\Sigma)=\prod_{i=1}^{79}f_{\mu^{1},\Sigma}(x^{i})\times\prod_{j=1}^{61}f_{\mu^{2},\Sigma}(x^{79+j})\]

协方差矩阵可以直接按样本数量加权和
统一协方差矩阵后，其实如果进行化简会发现此时依旧是一个线性模型，即wx+b形式的模型

在统计学中，方差是用来度量单个随机变量的离散程度，而协方差则一般用来刻画两个随机变量的相似程度

以上两种model，其实逻辑回归的准确率在宝可梦数据集上略好于概率分布，这可能是因为概率模型会预先假设数据符合一种概率分布，因此概率模型相对更适合模型数量少或者有一定noise的情况

softmax

前两个模型考虑了二分的情况，那么多个类别呢？这时仍然需要模型输出概率，但是概率总和需要小于等于1，然后选一个最高的作为输出；问题变成了如何得到这样的概率，可以用softmax
对每个输出值 \(o_j\) 预测概率值 \(\hat y_j\) 可以这么得到：
\[ {\hat{y} }_{j}={\frac{\exp(o_{j})}{\sum_{k}\exp(o_{k})} } \]
\(\hat y_j\) 可以视为对给定任意输入x的每个类的条件概率，即P(y = 某类 | x)
整个数据集的条件概率为：
\[P({\bf Y}\mid{\bf X})=\prod_{i-1}^{n}P({\bf y}^{(i)}\mid{\bf x}^{(i)}).\]
根据最大似然估计,我们最大化P(Y|X),相当于最小化所有子概率的负对数和
\[ -\log P(\mathbf{Y}\mid\mathbf{X})=\sum_{i=1}^{n}-\log P(\mathbf{y}^{(i)}\mid\mathbf{x}^{(i)})=\sum_{i=1}^{n}l(\mathbf{y}^{(i)},{\hat{\mathbf{y} } }^{(i)}) \]
其中的损失函数是交叉熵
\[l({\bf y},\hat{\bf y})=-\sum_{j=1}^{q}y_{j}\log\hat{y}_{j}.\] $$\begin{align} l({\bf y},\hat{\bf y})= -\sum_{j=1}^{q}y_{j}\log{\frac{\exp(o_{j})}{\sum_{k=1}^{q}\exp(o_{k})}} \\ =\sum_{j=1}^{q}y_{j}\log\sum_{k=1}^{q}\exp(o_{k})-\sum_{j=1}^{q}y_{j}o_{j} \\ =\log\sum_{k=1}^{q}\exp(o_{k})-\sum_{j=1}^{q}y_{j}o_{j}. \end{align}$$ $$ \partial_{o_{j}l}({\bf y},\hat{\bf y})=\frac{\exp(o_{j})}{\sum_{k=1}^{q}\exp(o_{k})}-y_{j}=\mathrm{sofmax}({\bf o})_{j}-y_{j} $$

softmax是一个非线性函数,但softmax回归的输出仍然由输入特征的仿射变换(保持点、直线和面之间相对关系的变换)决定，因此,softmax回归是一个线性模型
看上去很巧，导数就是softmax模型分配的概率与实际发生的情况(由独热标签向量表示)之间的差异 数学原理

优化技巧

训练效果取决于很多因素，常见的排查思路有：

• Model Bias: 训练数据有一定倾向性，实际的function set过于小以致于没有理想的函数，此时可能需要增加参数或者增加数据量
• 局部最小值和鞍点: 可以用泰勒公式估算附近的函数值，这两种点的梯度(一阶导)都是0，区别在于二阶导数，如果恒非正/非负，就是极值，否则就是鞍点
  • 令附近点与求导的点之间的向量为v,泰勒公式的二阶项可以写成 \(v^THv\) 的形式(H是对各个w的二阶导数项组成的句子)，用线代的指示，该式恒非正/非负等价于H的特征值恒非正/非负
    • 这样一来，对鞍点，设H的特征向量为u， \(u^THu = \lambda||u||^2\) , 沿着为负的特征向量方向就能继续下降
  • 另一种思路是所谓的动量，动量本质上是之前的梯度的加权和，类比物理上的动量，能一定程度上保持训练整体的倾向,将其与当前梯度相加,能一定程度上帮助跳出局部最低点
• 有时静态的更新很难达到最低点(更新快会遇到不同参数收敛速度不同导致的震荡，慢会龟速爬行)，因此需要动态的更新机制: \(\theta_{i}^{t+1}\leftarrow\theta_{i}^{t}-\frac{\eta}{\sigma_{i}^{t} }\,g_{i}^{t}\) 其中 \(\sigma_{i}^{t}=\sqrt{\frac{1}{t+1} \sum_{i=0}^{t}(g_{i}^{t})^{2} }\) \(g_{i}^{t}=\frac{\partial L}{\partial\theta_{i}}|_{\theta=\theta^{t}}\) (adagrad)
  • 但依然有问题: 同一个参数在不同的取值范围内收敛速度也不同，因此需要进一步的动态机制(RMS Prop): \(\theta_{i}^{t+1}\leftarrow\theta_{i}^{t}-\frac{\eta}{\sigma_{i}^{t}}\,g_{i}^{t}\quad\sigma_{i}^{t}=\sqrt{\alpha\!\left(\sigma_{i}^{t-1}\right)^{2}+(1-\alpha)\!\left(g_i^{t}\right)^{2}}\) 从而让最近的梯度影响更大
  • 著名的adam就是同时用了 momentum和 RMS Prop,动量与 \(\sigma\) 的不同是: 动量考虑方向,而后者只考虑大小
• 上述方法还是会有震荡,只不过震荡会最后收敛,因此考虑能否动态调整学习率
  • 最常见的做法是学习率衰减learning rate decay
  • warm up,也就是让学习率先快后慢,很难解释,但先快后慢的warmup在很多知名模型里表现很好

一般来说,adam比SGDM(使用动量的sgd)速度快,但最后收敛的效果差一点,这两者可以说是两个极端,常用的优化策略会在两者间折中或者微调,但可解释性嘛,都很难说 以下简单的记录一些相关方法:

adam部分:

• SWATS: 朴素的方法,先用adam快速逼近目标,再用sgdm慢慢收敛
• AMSGrad: 某些局部的梯度可能会超过几个数量级的高,因但由于adam算的是平方均根,这个局部梯度影响会非常有限,(例如a比b小100倍,平方根只差10倍,100个a的梯度却大于一个b的梯度) 因此可以记住一个历史最大值,从而相对扩大大梯度的影响力, 这样的话连续遇到小梯度学习率不会减少, \({ {\theta_{t}=\theta_{t-1}-\frac{p}{\sqrt{\hat{v}_{t}+\varepsilon}}m_{t}\space\space } } { {\hat{v}_{t}=\operatorname*{max}(\hat{v}_{t-1},v_{t})} }\) 但这其实没有解决adagrad学习率不断衰减的问题,只是延缓了
• AdaBound: 给learning rate设置上下限(clip函数),简单粗暴,可解释性也很迷
• cyclicalLR: 让lr周期性波动,简单的线性波动或者cos函数都可以,lr大是探索性的,小是寻找收敛点,类似的有SGDR,One-cycle LR等

RAdam: 用于解决训练初期梯度方差大,先用sgdm积累足够的样本,再转到类似adam的方法,同时让非初期的梯度有更高影响力
假设梯度是取样于一种分布,因此参数只和取样次数t有关,学习率满足以下条件,其中rt是恒增的

\[\begin{array}{c}{ {\rho_{t}=\rho_{\infty}-\frac{2t\beta_{2}^{\ t} }{1-\beta_{2}^{\ 2} } } }\\ { {\rho_{\infty}=\displaystyle\frac{2}{1-\beta_{2}^{\prime} }-1} }\\ r_{t}={\sqrt{\frac{(\rho_{t}-4)(\rho_{t}-2)\rho_{\infty} } {(\rho_{\infty}-4)(\rho_{\infty}-2)\rho_{t} } } } \end{array}\]

\[\theta_{t}=\theta_{t-1}-\eta\hat{m}_{t} \space when \space 𝜌𝑡 ≤ 4\]

\[\theta_{t}=\theta_{t-1}-{\frac{\eta r_{t} }{ {\sqrt{\hat{v} }_{t}+\varepsilon} } }\,{\hat{m} }_{t} \space when \space 𝜌𝑡 > 4\]

这是一个比较保守的策略,防止太过激进的学习

动量相关:

• Nesterov accelerated gradient (NAG): 与普通动量法区别是,用动量来预测下一个参数位置,通过预测位置的梯度更新参数 \(m_{t}={\lambda}m_{t-1}+\eta\nabla L(\theta_{t-1}-\lambda m_{t-1})\)

其他:

• Lookahead: 一种很抽象的方法,不管用什么优化方法,每轮中走k步到一个理论上的终点,在起点和终点间找一个点作为实际终点
  
• Shuffling,Dropout,Gradient noise: 这些都是增加随机性的方法
• Warm-up,Curriculum learning(先学容易的数据),Fine-tuning(使用预训练的模型)

经验上,cv用sgdm多一点;nlp,gan用adam多一点

Normalization

为了处理不同维度上输入规模不一的问题,需要归一化
Feature Normalization: 我们把统一维度的x输入视为正态分布的,令 \(\widetilde{x}_{i}^{r}\leftarrow{\frac{x_{i}^{r}-m_{i} }{\sigma_{i}} }\) 其中m为平均数,𝜎是标准差
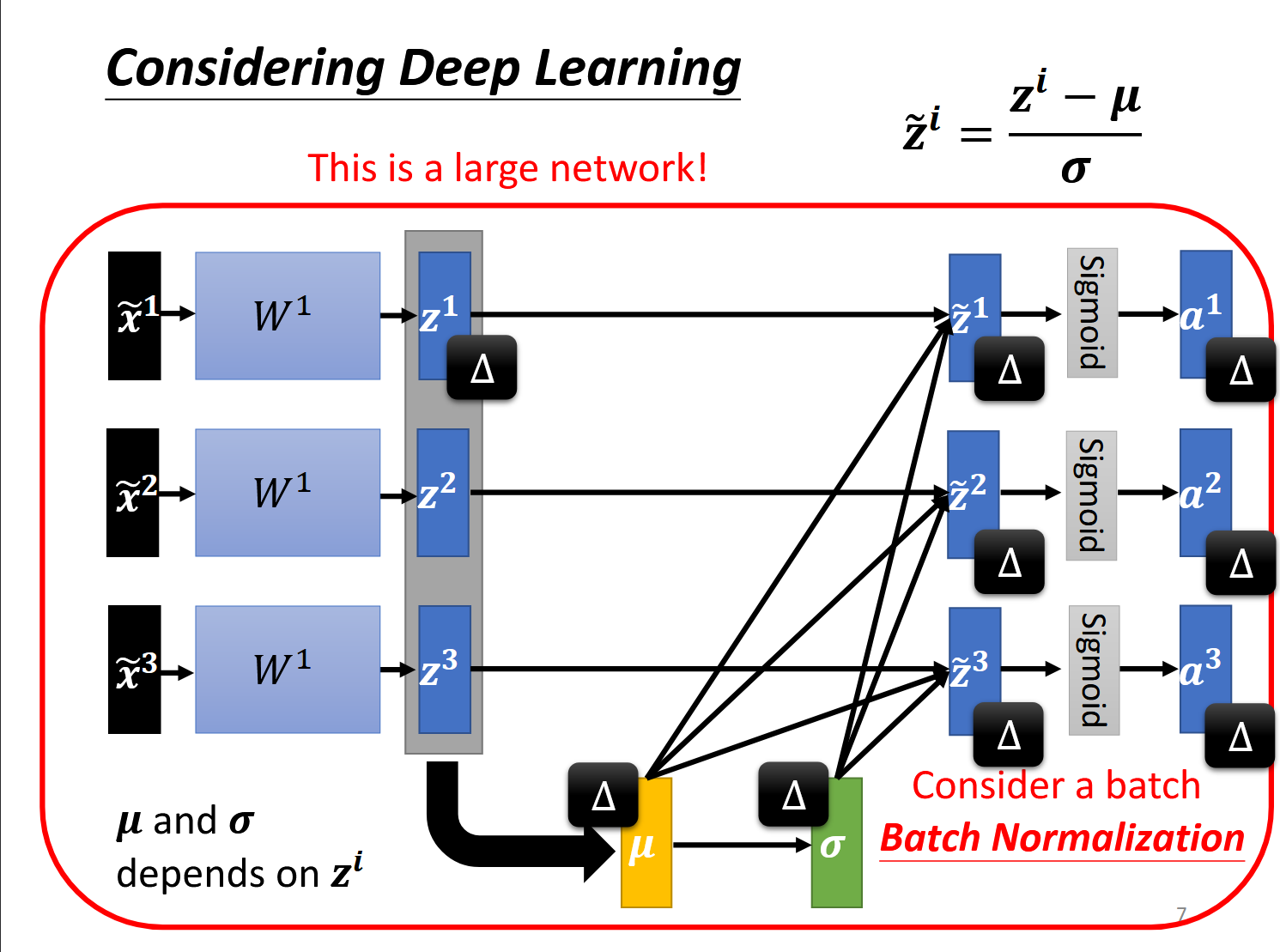
当然也可以对与w的加权和z向量做归一化: \({\tilde{z}}^{i}=\frac{z^{i}-\mu}{\sigma}\)
然后令 \(z^{i}=\gamma\Theta\widetilde{z}^{i}+\beta\) , 其中γ初始为1,β初始为0,这两个是学习参数,用于在之后调整分布
这样的归一化计算量较大,实际中一般只对batch做归一化

卷积神经网络CNN

名词解释:

• Receptive Field（感受野）: 字面意思,就是神经元的视野,cv中我们希望神经元各自只捕捉一个局部特征,一般感受野会是方形矩阵
  • 最常见的rf是覆盖所有维度(channel)的,也就是所有色彩空间,常见的rf是3×3,且会有复数的神经元
  • 共享参数: 即两个神经元用相同的参数,常见的共享方法是: 每个rf有n组神经元,不同的rf相同组序号的神经元共享参数;也可以理解为用不同的filter矩阵(也就是共享参数的神经元)做卷积
• stride(步幅): 感受野之间的步幅,例如一个rf对上的最左上元素是(i,j),下一个对上的左上元素就是(stride+i,j)
• padding: 由于内核矩阵以及步幅未必会让最后一步正好够运算,有时需要填充若干行/列,最常用的是直接填0
• pooling(池化): 在不改变关键信息的前提下尽可能简化输入规模,例如对规模是m×m的矩阵,对每个n×n的子矩阵取一个最大值,最后得到边长m/n的方阵
• flatten: 将最后的结果拉长为一维向量,用于之后的模型学习

基于以上限制,cnn的model bias其实相对较大,但在影像辨识中不是坏事

spatial transformer layer

鉴于CNN的特点,它对图片缩放,旋转,镜像后的数据,不会依旧保有识别能力.当然想处理这个问题很简单,把经过变化的图片也塞进训练集就可以了,但是这样会严重影响训练效率,而更好的做法是,增加一个图片变化层,用于转化图片到训练集的对应数据
对图片的每个像素,一个2×2的权重矩阵加一个2维的偏移向量就可以得出其对应像素,而对于非整数的对应坐标,出于可微性考虑,将其与周边点的距离积为权值乘以周边点的值,最后相加,如下所示:
\[\begin{array}{l}{ {a_{22}^{l}=(1-0.4)\times(1-0.4)\times{}(1-0.4)\times a_{22}^{l-1} } }\\ { {+(1-0.6)\times(1-0.4)\times(1-0.6)\times a_{12}^{l-1} } }\\ { {+(1-0.6)\times(1-0.6)\times(1-0.6)\times a_{23}^{l-1} } } \\ { +(1-\,0.4)\times(1-0.6)\times a_{23}^{l-1} } \end{array}\] 由于这样的取值是可微的,也就可以用梯度下降进行学习,将其嵌入神经网络中则可提高对变化后图片的识别效果

self-attention

sequence labeling: 即为输入序列中的每个元素分配一个标签,例如nlp中标注词性.这种问题的难点在于: 由于输入的向量长度不定,难以确定应该用什么规格的网络,于是需要注意力这种机制来让一个输入向量a能获取一些序列中的上下文信息形成向量b再进入网络
那么怎么让a携带上下文信息呢,常见的思路有做加权和(additive)或者加权积(dot-product),后者更常用,也就是输入向量各种乘以一个(互不相同的)权重,然后乘在一起
s-a层所做的运算如下图:

实际上,该层学习的就是三个权值矩阵

相关技术:

• Multi-head Self-attention: 简单地说就是用两个独立的注意力神经,其产物算加权和作为最终输出
• Positional Encoding: 为了弥补注意力没有位置信息的问题,最早的处理是对输入ai加上一个ei偏置,后续发展中有不同的添加位置信息的方法
• Truncated Self-attention: 对语音这种规模很大的输入,出于效率考虑,可以减少注意力计算的范围,只看很小的上下文
• CNN: cnn可以视为注意力的一种特例
• RNN: 相比rnn,注意力在并行性,以及对上下文信息的利用能力上都相对更好

变形金刚

transformer,下文简称tf,是一种seq2seq模型,这种模型有相当广泛的应用,语音辨识/合成,句法分析,目标检测,以及现在热门的对话生成都可以使用

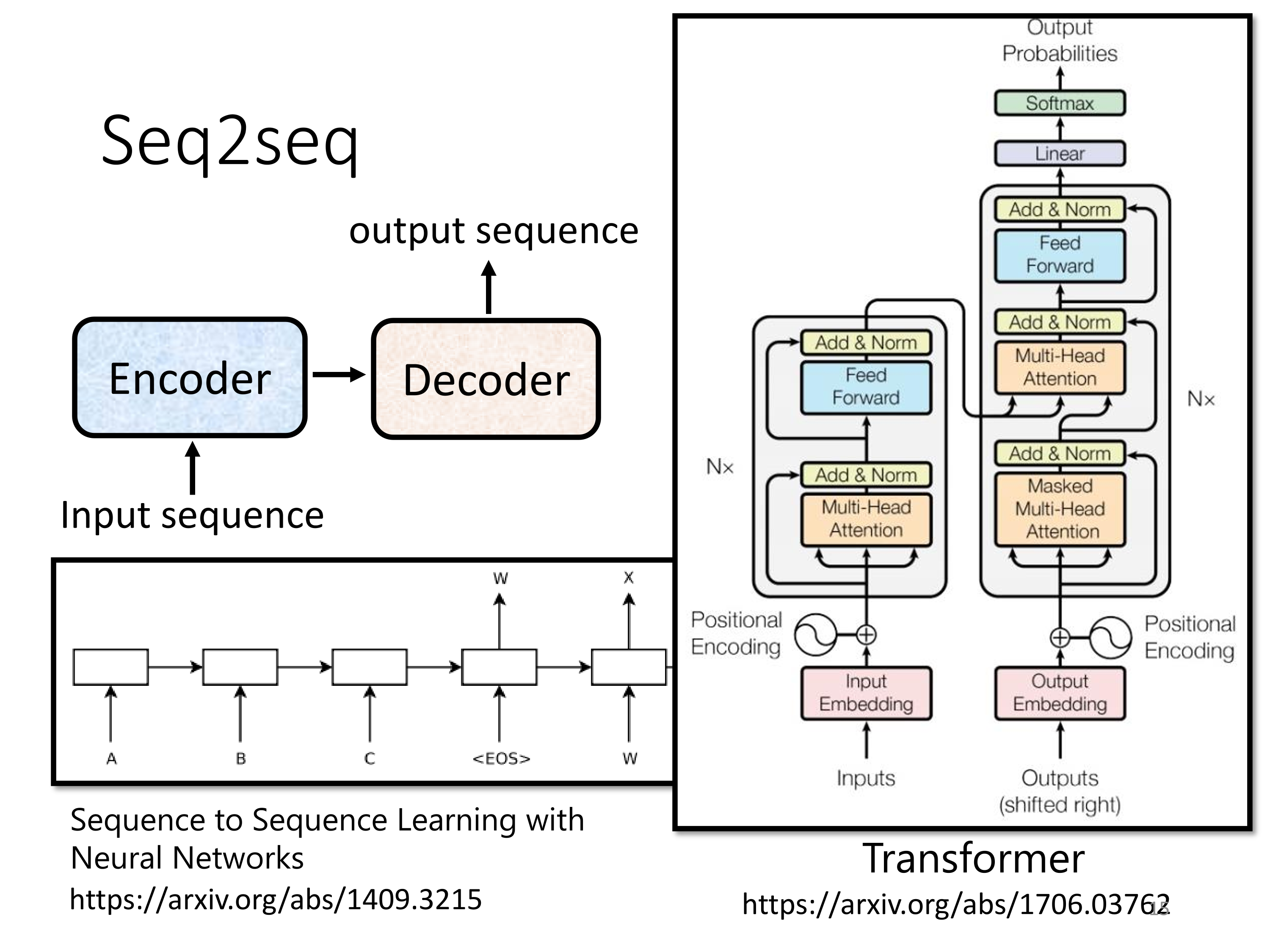
tf的架构相当复杂,这里简单地描述一下:其主要用en/decoder组成,encoder中有很多block用于生成中间向量,每层block先做一次注意力(结果向量加上输入向量,这叫做residual connection,随后做一次layer normalization),再用全连接(fc)网络计算,这个fc网络也会用residual
decoder除了接受encoder数据外,还要接受一个表示开始产生输出的符号(bos),这个符号可以用one-hot表示,类似rnn,dec不断把自己的输出当做下一轮的输入,如果输出一个终止符来结束,就叫Autoregressive;而Non-autoregressive则一次生成所有输出,一个输入对应一个输出,为此需要一个分类器来产生长或者一个足够长的默认长度,让机器自己选一个槽位输出终止符,这样的好处是并行化且容易控制长度,缺点则是表现差
关于dec的架构,观察其与enc不同,首先是注意力层多了masked前缀,这个掩码就是让所有输入维度的注意力只能注意自己极其以前的输入(由于decoder输出有顺序,这样很符合直觉)
关于两者的交互,看下面的图比较直观,不太准确的说就是同时用双方的数据不断地做masked 注意力(输出会不断作为下一轮输入加进来),这叫做Cross Attention
原始论文中dec不断从enc的最后一层拿数据,但也有论文会对应着拿

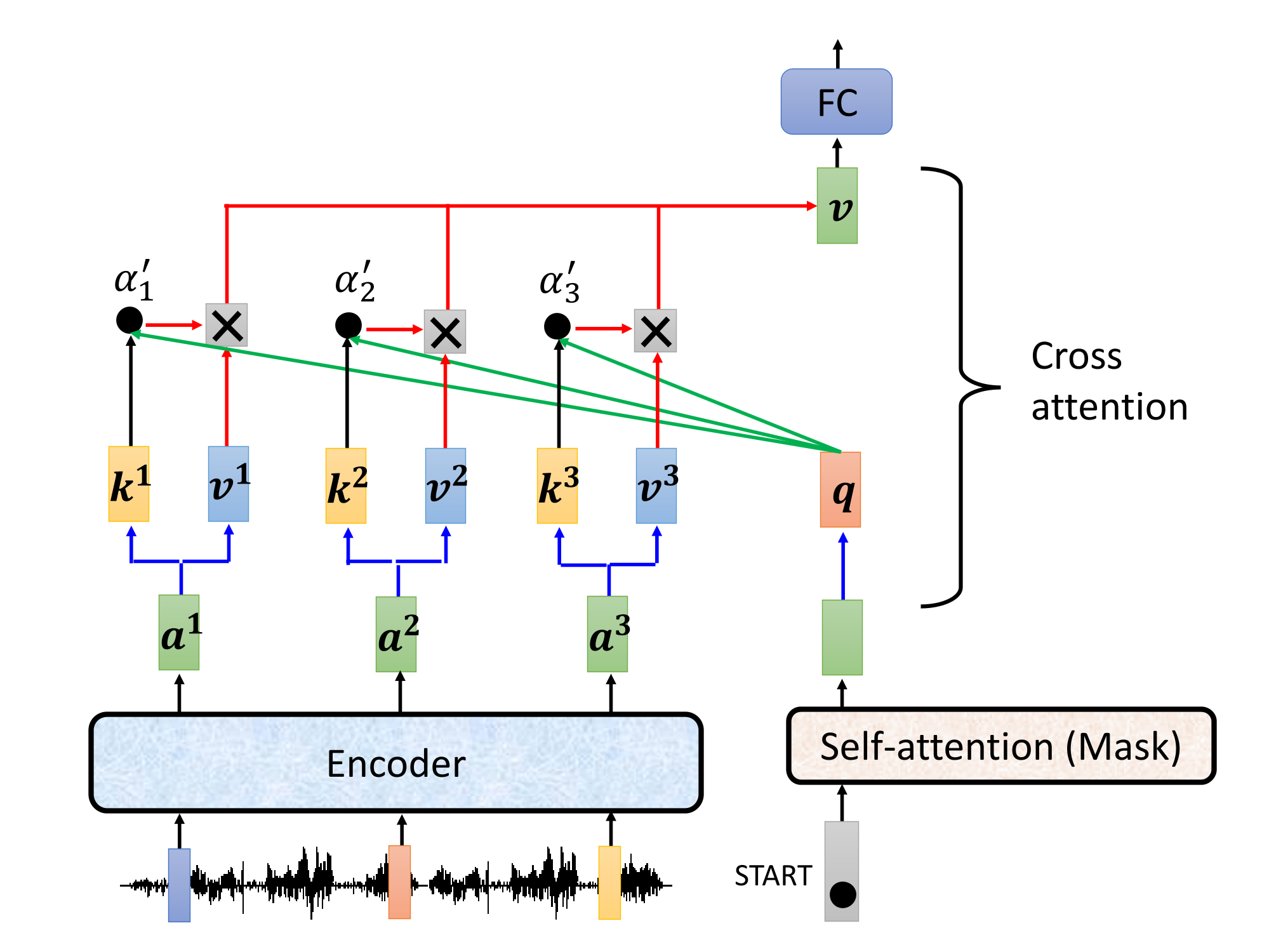
相关技术:

• Teacher Forcing: 简单地说就是训练时直接将答案作为dec输入
• Copy Mechanism: 从输入中复制文字给输出用的能力
• Guided Attention: 对一些规则严格的场景,可以直接对训练中的模型加以限制,例如语音合成
• Beam Search: 一种常用于序列预测任务的搜索算法,能在一定程度上预测相对更优的序列/路径
• exposure bias: dec辨识错误的能力差,导致一步错步步错,解决方法是增加一些Noise
• Scheduled Sampling: 在训练过程中,逐步减小使用真实目标序列的概率

bert

bert,目前很火的预训练seq2seq模型,是一种无监督学习模型,也就是没有label数据,其特点是训练中使用掩码数据(Masking Input),也就是遮住输入的部分字词,而加上遮住数据的完整输入就是我们希望bert能输出的结果,而损失函数也可以比较方便地用交叉熵(可以理解为以所有字符为类别的分类问题)
bert是基于tf的,其架构和tf类似,区别就是用掩码机制来无监督学习,由于不需要标注的数据集,bert很容易得到规模非常庞大的数据,因此有着很好的表现 除此以外有一些其他训练方法,如Next Sentence Prediction: 预测两个句子是否相接;Sentence order prediction:判断句子的顺序关系
在以下这些常见的一些基准测试中,bert都有不俗的表现:

• Corpus of Linguistic Acceptability (CoLA)
• Stanford Sentiment Treebank (SST-2)
• Microsoft Research Paraphrase Corpus (MRPC)
• Quora Question Pairs (QQP)
• Semantic Textual Similarity Benchmark (STS-B)
• Multi-Genre Natural Language Inference (MNLI)
• Question-answering NLI (QNLI)
• Recognizing Textual Entailment (RTE)
• Winograd NLI (WNLI)

尽管 BERT 的预训练是无监督的，但在特定下游任务（如文本分类、语法分析等）中(对这些下游任务来说,可以简单地给bert接上分类或者线性模型)，BERT 可以进行微调,这个过程是监督学习。微调阶段使用标注好的数据集，通过已知的标签来优化模型参数.所以如果想准确一点,可以叫半监督学习(semi)
bert的优异性能常常被归因于注意力对上下文的捕获能力以及大量的训练资料,但神奇的是用于做蛋白质分类效果也很好,英语Bert用在中文上效果也很好,这或许可以理解为这些有规律的编码作为语言其实在词义向量以及结构上有相似之处,根据李老师自己的实验,这种神奇的能力只会出现在足够大的训练集上

RNN

相关场景:

slot filling: 类似一个分类问题,将给定输入向量(一句话)中的词语分类到特定的槽位去

rnn用于解决输入向量间有顺序关系的问题,普通的前馈网络所有输入的词语都是地位相同的,因此很难捕捉文字的前后语义关系,于是产生了rnn这种方法,也就是把前面的计算结果作为之后的输入,常见的类型有:

• 简单rnn
  • elman network: 先前的隐藏层计算结果存起来,后面被下一个神经元的隐藏层调用
  • jordan network: 将前一个神经元的输出存起来,被下一个神经元调用
• 其他
  • Bidirectional RNN: 训练正向和反向的两个rnn,最后的输出算加权和

Long Short-term Memory (LSTM)

简单地说就是用两个阀门控制是否存入或放出历史信息,一个阀门控制是否遗忘已有的信息,阀门的开闭让网络学习
其训练过程相对来说比较繁琐,还好李老师细心地做了流程图,这里直接贴上来

LSTM的缺点是过于复杂导致计算成本高,因此有Gated Recurrent Unit (GRU)这样的简化版本(三个gate)

问题

1. RNN会复用之前的模型,例如其权值w,这会导致层数上来后,后面神经的权值会产生幂函数关系,使loss surface非常陡峭
   更准确地说,由于幂函数的特性,w小会很容易梯度消失,w大则非常陡峭,LSTM可以一定程度上解决前一个问题,因为它能存储历史信息更长时间
   而后一个问题,工程上最实用的方法是clip设置上界

2. 鉴于rnn的特性,处理不定长的输入(向量)是很方便的,但如何处理不定长的输出呢?
   例如语音识别,对若干音频输入,简单的想法是每个音频输出一个字符,结果把每个输出的重复部分拿掉,但如何处理叠词呢?
   可以用一个φ符号代表null,也就是分割符,φ间的有意义输出作为识别结果,下一个问题是,音频可能切的很碎,不能保证对应关系具体应该怎么排
   为此需要Connectionist Temporal Classification (CTC)简单地说就是穷举可能的排列(实际会用dp优化),选取其中最多的一种(即概率最大的排列/对应关系)

以上讨论的语音识别其实有一个预设--识别结果的字符数≤音频样本数,对没有这种条件的问题,例如机器翻译该怎么做呢?
由于是循环的,rnn可以不断地产生输出,只需要一个特殊的表示结束的符号就可以,例如===

深度学习

Q: 为什么要深度,为什么要用那么多隐藏层而不是一个很宽的单层网络?
A: 深度学习能增加预测函数的弹性,这是因为它可以复杂的不同线性关系去拟合数据,那么为什么要用很深的网络?实际上,相同神经数量且较浅的网络预测效果会不如dl,也就是dl能用相对更少的参数拟合数据,因此更不容易overfitting,有更好的准确率;而dl的这种高效其实类似编程中的依赖关系,例如某个节点的后继节点都可以依赖于前一个节点,而整段程序只需要保留这个被多重依赖的节点的一个副本,节省大量空间,dl中其实也可能存在对某个前继神经的依赖关系,也就是dl是一个有结构上关系的网络

概念

对于复杂的网络,会使用神经网络块(block)来描述若干个网络层的组合,一般来说,块有自己的参数,前向传播,反向传播函数,这是一个逻辑概念,torch中可以用模块或者seq来实现

• torch.nn.Module: Base class for all neural network modules.Your models should also subclass this class.即所有模型的基类
• torch.nn.Sequential: Modules will be added to it in the order they are passed in the constructor. 有顺序的module的容器,与ModuleList的是它提供对内置模块的顺序调用,也就是已经实现了前向传播,因此它很适合用来定义一个block
• torch.nn.ModuleList:Holds submodules in a list. 模块的list,和普通的list没什么区别,有索引顺序,但并没有逻辑上的顺序

技术

生成模型

VAE 变分自编码器

对于生成任务，有一套直白的思路： 对一群数据提取特征，编码为一种分布，然后在生成时从分布中采样作为解码
若输入的数据为x, 编码出的隐式数据为x, p(z|x)称为后验概率，也就是给定发生了什么得到的估计；p(x|z)称为似然，也就是根据已有知识，对应该发生什么的估计
现在的问题是，如何得到一个性质良好的z，这个良好指两方面:

1. 解码(重建)时还原程度高
2. 在通过对隐空间采样来反向预测x时也有良好的表现

为此，VAE用高斯分布建模一个隐式空间，且定义其loss如下:

\(\mathcal{L}(x)=\mathbb{E}_{q(z|x)}\left[\log p(x|z)\right]-{ { {\operatorname{KL}(q(z|x)\ |\ p(z))}}}\)

这个loss想实现的目的是，在分布散度差距和还原损失之间取得平衡
我们要学习的参数是方差和均值，那么怎么做呢？这里引入一个 \(\epsilon\) 表示对标准正态分布的随机采样，将其乘方差再加上均值，就得到了一个模拟的采样结果可用于求梯度

flow-based model

Normalizing flow

主要参考李宏毅老师的视频以及一篇博文

在数学上，生成模型其实生成的是概率分布，一般将输入数据视为对某种分布的采样，用来学习一种分布G，最后再对学习的分布G随机采样来得到新的生成数据
这种所谓的随机采样，可以理解为对一种分布例如常见的正态分布采样，将这个采样的数据映射到我们学习到的分布G上，我们希望G的分布和真实数据的分布(这个分布是假想的)越接近越好，例如上面的VAE就会不断约束G的重构损失和KL散度
如果我们想直接优化分布之间的映射关系呢？

接下来需要引入一些前置知识:

Jacobian matrix 是一个数学概念，主要用于多变量微积分和向量微分。在函数的多变量情况下，Jacobian 矩阵描述了函数的局部线性近似
对于一个从 \({R}^n\) 到 \({R}^m\) 的函数 ，其 Jacobian 矩阵 ( J ) 定义为函数在某一点的偏导数矩阵。矩阵的元素形式如下：

\[ \begin{bmatrix} \frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} & \cdots & \frac{\partial f_1}{\partial x_n} \\ \frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} & \cdots & \frac{\partial f_2}{\partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial f_m}{\partial x_1} & \frac{\partial f_m}{\partial x_2} & \cdots & \frac{\partial f_m}{\partial x_n} \end{bmatrix} \] 此外，逆函数的J矩阵也互逆

行列式学过线代的都知道，其几何意义可以粗略理解为一个任意维度空间中的，矩阵所描绘的几何体的"体积"

那么，开始讨论概率分布的转化方法，给定随机变量z，及其概率密度函数π(z)，将其的分布转化为另一种分布实际上就是一种映射，设这个映射函数为f, 即 \(x=f(z)\) ，X是转化出的新变量，其概率密度函数为p(x)
那么对这个映射，我们知道所有概率函数的积分总和为1，也就是面积在映射中是不变的，那么基于常识让 \(p(x)dx=\pi (z)dz\)
而对向量的映射，其实也类似，只不过z对应向量的微分乘积会对应到x对应向量矩阵的行列式
代入和化简后得到:
\[p(x^{\prime})=\pi(z^{\prime})\left|\frac{1}{d e t(J_{f})}\right|\] 由于互逆矩阵的det乘积为1且J矩阵的逆矩阵和对应逆函数的J矩阵相同,也可以写成

\[p(x^{\prime})=\pi(z^{\prime}){\big|}d e t{\big(}J_{f^{-1}}{\big)}{\big|}\]

其实这个式子很直观，J矩阵里是x对z的微分，那么其逆矩阵就是z对x的微分，那么其行列式可以理解为映射中，z的“底面积"对应x”底面积"的比例关系(而“高"就对应概率本身)
基于这个数学式的生成模型称为G，即G将π(z)(通常是对正态分布取样)转化为一个概率分布p(x),可以形象地写作 \(x=G(z) \space | \space z=G^{-1}(x)\)

先前的表达式的对数形式为:
\(l o g p_{G}(x^{i})=l o g\pi\left(G^{-1}(x^{i})\right)+l o g|d e t(J_{G^{-1}})|\)
由于π一般是一个正态分布，第一项会倾向于在中间(标准正态分布就是0向量附近)取点，第二项表示的可以某种意义上理解为映射后微分空间的分散的程度的对数，如果总在中间取点，几乎没有分散，则对数是很小的负数，产生很大的惩罚;因此这样的形式能一定程度上约束分布不要过于集中

目前为止我们得到了一个优雅的数学式，但与常见的ml模型不同的是，在这个情况下(需要x,z相互可逆)，x、z有相同的长度，这产生了两个问题：

1. 计算量大
2. 对模型的约束较大，可能会降低泛化能力

这就是为什么名字叫flow了，因为我们会用一串G来弥补模型弹性不足的问题,为什么可以这样做？对z的变化可以说是链式的，在微分层面可以很直接地表示为多个J矩阵行列式对p(z)连乘，用一个对数函数就可以转化为连加,因此实际上用一个G和一连串G除了计算量没有本质区别，以下讨论一个G的情况
对一个具体的G，实际训练时考虑到计算量，会使用coupling layer这样的技术，它巧妙地牺牲一部分输入数据(不做变换仅复制)让涉及到的行列式和逆矩阵都很容易计算;也可以用一对一的卷积，对其内核矩阵(涉及的论文里是3×3)算行列式以及微分

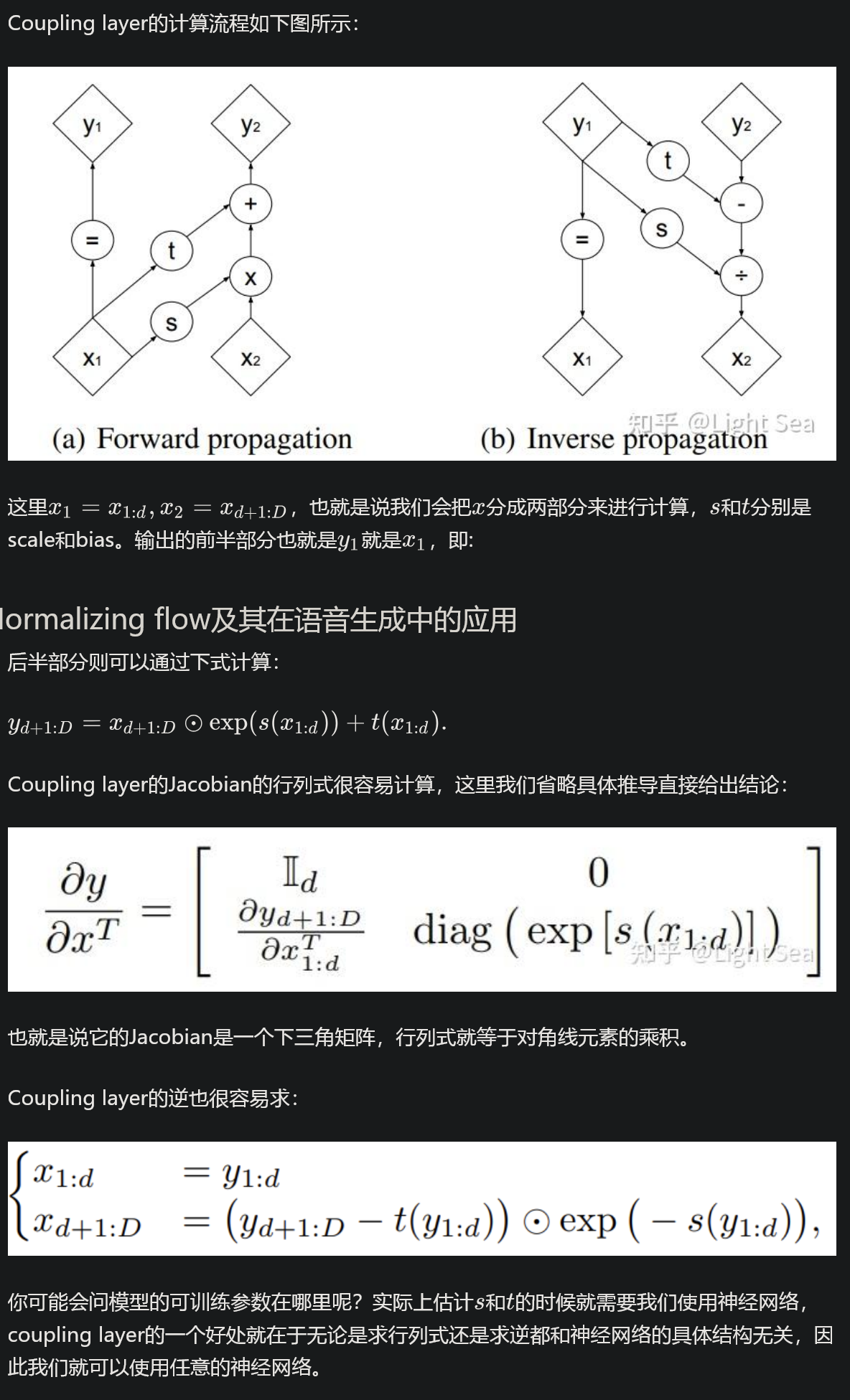
Flow Matching

数学

常微分方程: 形如 \({\frac{d y(t)}{d t}}\,=\,f(y(t),t)\)

其中,t为时间，f描述y与t的关系且可微分，一般来说y是需要求解的量
例如如果已知一个初始值，可以写作: \(y(t_{1})=y_{t_{0}}+\int_{t_{0}}^{t_{1}}f(y(t),t)d t\)
对复杂的神经网络，很多时候不能也没有必要求解析解，可以用一些数值方法估算：

• Euler Method: 直接用区间面积的和估算，形如 \(y(t_{1})\approx y(t_{0})+\sum_{i=0}^{N-1}h f(y(t_{0}+i h),t_{0}+i h)\) 其中h是区间宽度
• Neural ODE: 使用例如residual network之类的网络求解，这里不详细介绍

向量场与流

参考博文

上文介绍的标准流是通过组合一系列的生成器获得表达能力的，而每个生成器通过微分矩阵来评估映射的性质，因此命名为flow很直观
而对flow来说，想到向量也很直观，CNF正是一种基于向量场的方法
为什么要用向量场呢？想象分布p是一群点，当然它可以是无数个，这些点我们希望能都被一一映射到另一个分布里去，这就像初中物理课做的磁场实验，改变电磁铁的通电流向(磁性)，在磁场的作用下铁屑们就会纷纷自己组成另一种形状
在这种场作用下的概率p的运动轨迹成为概率密度路径，与之前不同的是运动需要时间，这里引入一个时间t变量，范围是[0,1],此外概率函数自己的性质是p(x)对x的积分必定是1，即 \(\textstyle\int p_{t}(\mathbf{x})\mathrm{d}\mathbf{x}=1\)
接下来定义向量场为: \(\mathbf{u}:[0,1]\times\mathbb{R}^{d}\to\mathbb{R}^{d}\) u也可以理解为瞬时速度
那么u和p什么关系，作为计算机专业不用懂原理，但存在这么一个方程式:

\[\frac{\partial}{\partial t}p_{t}({\bf x})+\nabla\cdot(p_{t}({\bf x}){\bf u}_{t}({\bf x}))=0\]

需要注意概率密度路径与速度场不是一一对应的，不同的速度场可以产生相同的概率密度路径

接下来回归标题，标题的流flow正是运动时的轨迹，定义为: \(\frac{\partial}{\partial t}\phi_{t}({\bf x})={\bf u}_{t}(\phi_{t}({\bf x}))\) ,其中 \(\phi _t(x)\) 初值为x的粒子在t时刻运动到的位置,也就是对其在[0,t]积分就会得到t点位置和初始位置的位移
那么显然p和 \(\phi\) 之间也有关系，这里之间放出来:

\[ p_t(\mathbf x)=p_0(\boldsymbol\phi_t^{-1}(\mathbf x))\left|\det\left[\frac{\partial\boldsymbol\phi_t^{-1}}{\partial\mathbf x}(\mathbf x)\right]\right| \]

这称为push-forward方程，其中t时刻位于x位置处的粒子在0时刻的出发位置是 \(\boldsymbol\phi_t^{-1}(\mathbf x)\)

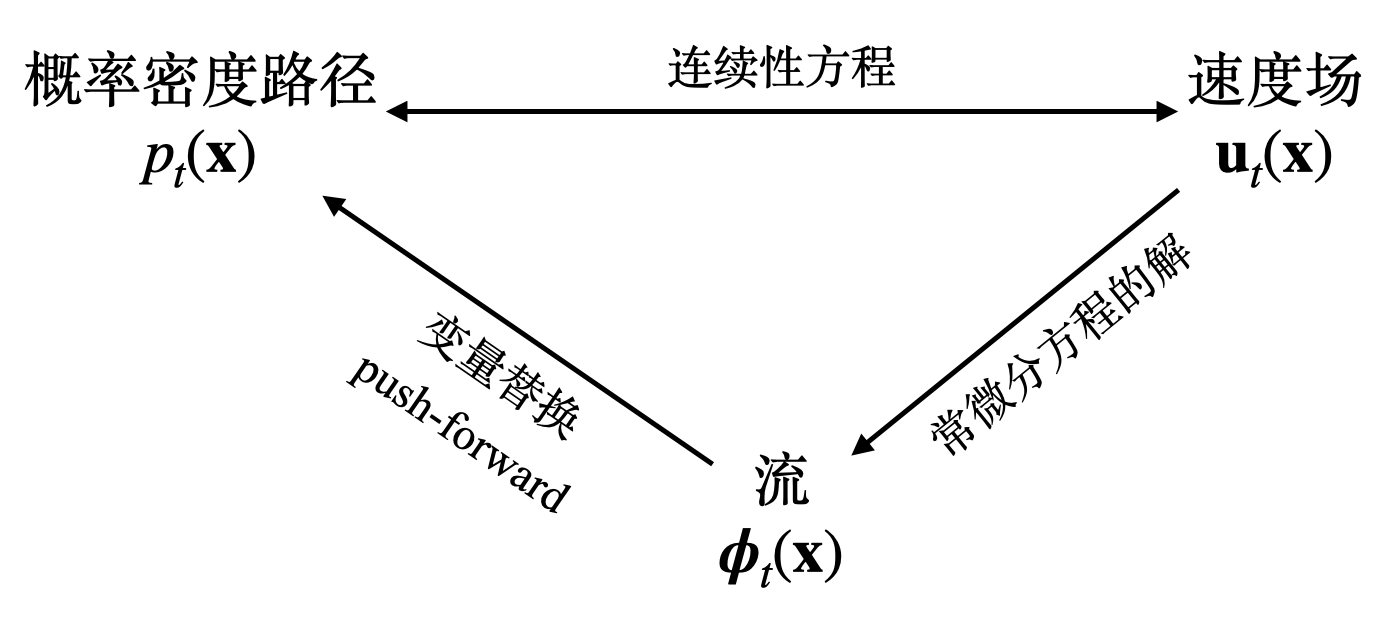
连续归一化流 (Continuous Normalizing Flows, CNFs)

终于说到生成模型了，令 \(p_t(x)\) 为概率密度路径，p0是一种简单分布(例如标准正态分布),p1是输入数据的分布, \(u_t(x)\) 为对应向量场，那么流匹配的模板就是用网络构建向量场 \(\mathbf v_{t}^{\theta}(\mathbf x)\) 去近似 \(u_t(x)\)
虽然一上来就定义了很多变量，但经过前文介绍，其实其目的很直观，接下来得到一个同样直观的损失函数:
\[\mathcal L_\text{FM}(\theta)=\mathbb E_{t,p_t(\mathbf x)}\left[\Vert\mathbf v_{t}^{\theta}(\mathbf x)-\mathbf u_t(\mathbf x)\Vert^2\right]\]

当然，真实速度场是未知的，这是生成模型的经典问题，同样一个经典解决方案，也就是每次取一个样本去近似，不断更新训练，这就需要条件速度场 给定某特定样本x1 ，称 \(p_t(x|x1)\) 为条件概率路径

\[p_t(\mathbf x)=\int p_t(\mathbf x\vert\mathbf x_1)q(\mathbf x_1)\mathrm d\mathbf x_1=\mathbb E_{q(\mathbf x_1)}[p_t(\mathbf x\vert\mathbf x_1)]\] \[\mathbf u_t(\mathbf x)=\int \mathbf u_t(\mathbf x\vert\mathbf x_1)\frac{p_t(\mathbf x\vert\mathbf x_1)q(\mathbf x_1)}{p_t(\mathbf x)}\mathrm d\mathbf x_1=\mathbb E_{p(\mathbf x_1\vert\mathbf x)}[\mathbf u_t(\mathbf x\vert\mathbf x_1)]\]

使用这种条件向量场更新的流匹配称为 conditional flow matching
其损失函数为:

\[\mathcal L_\text{CFM}(\theta)=\mathbb E_{t,q(\mathbf x_1),p_t(\mathbf x\vert\mathbf x_1)}\left[\Vert\mathbf v_{t}^{\theta}(\mathbf x)-\mathbf u_t(\mathbf x\vert\mathbf x_1)\Vert^2\right]\]

接下来只剩下具体的条件向量场设计问题了，详见博文