基于mit6.006和hello-algo的算法笔记

发表于 2024-01-20 更新于 2024-01-17 分类于课程笔记，数据结构与算法阅读次数：本文字数： 19k 阅读时长 ≈ 1:09

基础

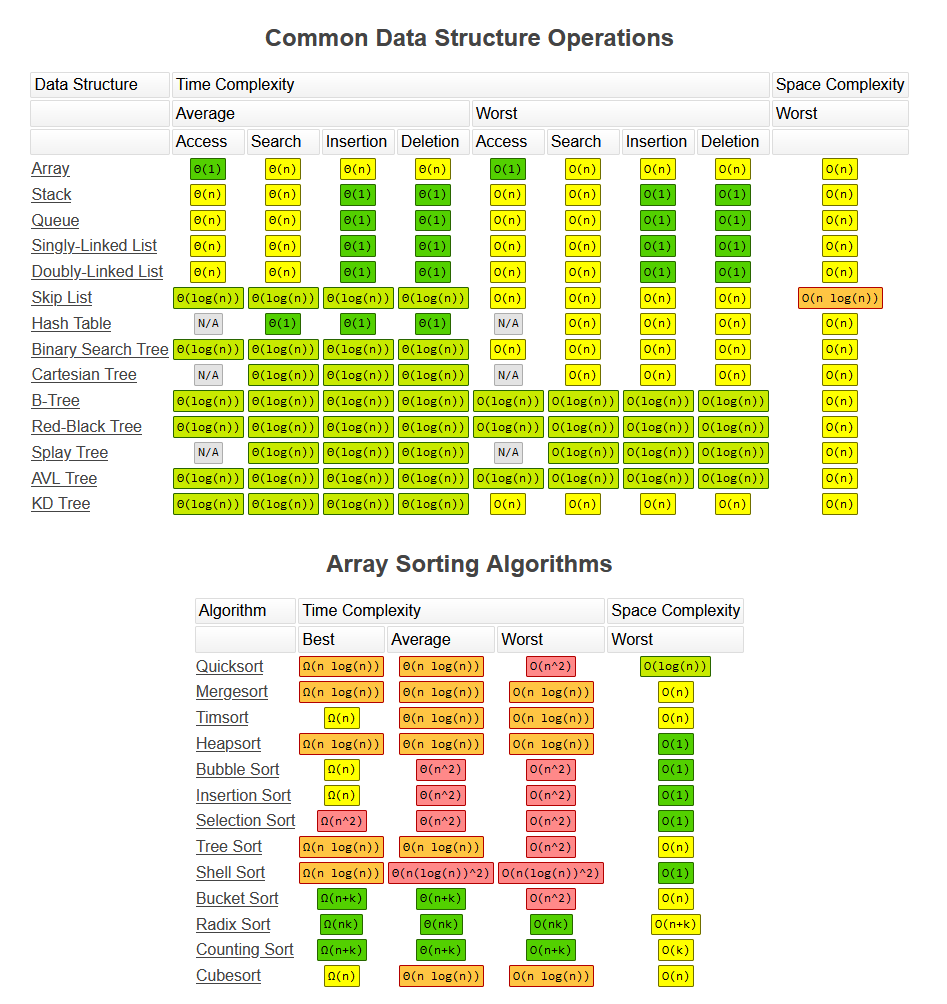
数据结构

算法性质

循环不变式主要用来帮助我们理解算法的正确性。关千循环不变式，我们必须证明三条
性质：
初始化：循环的第一次迭代之前，它为真。
保持：如果循环的某次迭代之前它为真，那么下次迭代之前它仍为真。
终止：在循环终止时，不变式为我们提供一个有用的性质，该性质有助千证明算法是正确的。

f(n) = O(g(n)) 类似于 a<=b

f(n) = Ω (g(n)) 类似于 a>=b

f(n) = θ (g(n)) 类似于 a=b

f(n) = o(g(n)) 类似于 a<b

f(n) = w(g(n)) 类似于 a>b

分治法（递归）

选择排序

在A[:i+1]内找到最大的元素，和A[i]交换
递归地排序A[:i]

def selection_sort(A, i = None): # T(i)
’’’Sort A[:i + 1]’’’
    if i is None: i = len(A) - 1 # O(1)
    if i > 0: # O(1)
        j = prefix_max(A, i) # S(i)
        A[i], A[j] = A[j], A[i] # O(1)
        selection_sort(A, i - 1) # T(i - 1)

def prefix_max(A, i): # S(i)找到最大元素的索引值
’’’Return index of maximum in A[:i + 1]’’’
    if i > 0: # O(1)
        j = prefix_max(A, i - 1) # S(i - 1)
        if A[i] < A[j]: # O(1)
            return j # O(1)
    return i # O(1)

python实现(迭代)：

def selection_sort(nums: list[int]):
    """选择排序"""
    n = len(nums)
    # 外循环：未排序区间为 [i, n-1]
    for i in range(n - 1):
        # 内循环：找到未排序区间内的最小元素
        k = i
        for j in range(i + 1, n):
            if nums[j] < nums[k]:
                k = j  # 记录最小元素的索引
        # 将该最小元素与未排序区间的首个元素交换
        nums[i], nums[k] = nums[k], nums[i]

• prefix max analysis:
– Base case: for i = 0, array has one element, so index of max is i
– Induction: assume correct for i, maximum is either the maximum of A[:i] or A[i],
returns correct index in either case
• selection sort analysis:
– Base case: for i = 0, array has one element so is sorted
– Induction: assume correct for i, last number of a sorted output is a largest number of
the array, and the algorithm puts one there; then A[:i] is sorted by inductio

性质：O(n^2)，非稳定原地排序

插入排序

类似扑克牌，从右侧选择未排序元素，逐个插入左侧的已排序部分

def insertion_sort(A, i = None): # T(i)
’’’Sort A[:i + 1]’’’
    if i is None: i = len(A) - 1 # O(1)
    if i > 0: # O(1)
        insertion_sort(A, i - 1) # T(i - 1)
        insert_last(A, i) # S(i)

def insert_last(A, i): # S(i)
’’’Sort A[:i + 1] assuming sorted A[:i]’’’
    if i > 0 and A[i] < A[i - 1]: # O(1)
        A[i], A[i - 1] = A[i - 1], A[i] # O(1)
        insert_last(A, i - 1) # S(i - 1)


• insert last analysis:
– Base case: for i = 0, array has one element so is sorted
– Induction: assume correct for i, if A[i] >= A[i - 1], array is sorted; otherwise,
swapping last two elements allows us to sort A[:i] by induction

• insertion sort analysis:
– Base case: for i = 0, array has one element so is sorted
– Induction: assume correct for i, algorithm sorts A[:i] by induction, and then
insert last correctly sorts the rest as proved above

python实现（迭代）：

def insertion_sort(nums: list[int]):
    """插入排序"""
    # 外循环：已排序区间为 [0, i-1]
    for i in range(1, len(nums)):
        base = nums[i]
        j = i - 1
        # 内循环：将 base 插入到已排序区间 [0, i-1] 中的正确位置
        while j >= 0 and nums[j] > base:
            nums[j + 1] = nums[j]  # 将 nums[j] 向右移动一位
            j -= 1
        nums[j + 1] = base  # 将 base 赋值到正确位置

特性：复杂度O(n^2)，原地稳定排序

归并排序

def merge_sort(A, a = 0, b = None): # T(b - a = n)
’’’Sort A[a:b]’’’
    if b is None: b = len(A) # O(1)
    if 1 < b - a: # O(1)
        c = (a + b + 1) // 2 # O(1)
        merge_sort(A, a, c) # T(n / 2)
        merge_sort(A, c, b) # T(n / 2)
        L, R = A[a:c], A[c:b] # O(n)
        merge(L, R, A, len(L), len(R), a, b) # S(n)

def merge(L, R, A, i, j, a, b): # S(b - a = n)
’’’Merge sorted L[:i] and R[:j] into A[a:b]’’’
    if a < b: # O(1)
        if (j <= 0) or (i > 0 and L[i - 1] > R[j - 1]): # O(1)
            A[b - 1] = L[i - 1] # O(1)
            i = i - 1 # O(1)
    else: # O(1)
        A[b - 1] = R[j - 1] # O(1)
        j = j - 1 # O(1)
    merge(L, R, A, i, j, a, b - 1)

• merge analysis:
– Base case: for n = 0, arrays are empty, so vacuously correct
– Induction: assume correct for n, item in A[r] must be a largest number from remaining
prefixes of L and R, and since they are sorted, taking largest of last items suffices;
remainder is merged by induction
 merge sort analysis:
– Base case: for n = 1, array has one element so is sorted
– Induction: assume correct for k < n, algorithm sorts smaller halves by induction, and then merge merges into a sorted array as proved above.

python实现：

def merge(nums: list[int], left: int, mid: int, right: int):
    """合并左子数组和右子数组"""
    # 左子数组区间 [left, mid], 右子数组区间 [mid+1, right]
    # 创建一个临时数组 tmp ，用于存放合并后的结果
    tmp = [0] * (right - left + 1)
    # 初始化左子数组和右子数组的起始索引
    i, j, k = left, mid + 1, 0
    # 当左右子数组都还有元素时，比较并将较小的元素复制到临时数组中
    while i <= mid and j <= right:
        if nums[i] <= nums[j]:
            tmp[k] = nums[i]
            i += 1
        else:
            tmp[k] = nums[j]
            j += 1
        k += 1
    # 将左子数组和右子数组的剩余元素复制到临时数组中
    while i <= mid:
        tmp[k] = nums[i]
        i += 1
        k += 1
    while j <= right:
        tmp[k] = nums[j]
        j += 1
        k += 1
    # 将临时数组 tmp 中的元素复制回原数组 nums 的对应区间
    for k in range(0, len(tmp)):
        nums[left + k] = tmp[k]

def merge_sort(nums: list[int], left: int, right: int):
    """归并排序"""
    # 终止条件
    if left >= right:
        return  # 当子数组长度为 1 时终止递归
    # 划分阶段
    mid = (left + right) // 2  # 计算中点
    merge_sort(nums, left, mid)  # 递归左子数组
    merge_sort(nums, mid + 1, right)  # 递归右子数组
    # 合并阶段
    merge(nums, left, mid, right)

特性：O(nlgn)，稳定排序

寻峰算法

一维情况：实际上是一种二分查找，先查看中点是不是峰值，如果不是则选取邻居节点较大的一侧递归寻找复杂度lgn

二维情况下：

• Pick middle column j = m/2
• Find global maximum on column j at (i, j)
• Compare (i, j − 1), (i, j), (i, j + 1)
• Pick left columns of (i, j − 1) > (i, j)
• Similarly for right
• (i, j) is a 2D-peak if neither condition holds
• Solve the new problem with half the number of columns.
• When you have a single column, find global maximum and you‘re done.

T (n, m) = T (n, m/2) + Θ(n) (to find global maximum on a column — (n rows))
T (n, m) = (Θ(n) + . . . + Θ(n))log m= Θ(n log m) = Θ(n log n) if m = n

这种解法思路是：

对数组的中间一列寻找最大值
如果最大值是峰值，可以返回
否则对数组最大的邻居所在的一侧进行递归(即子问题大小为原来的一半)

除此以外还有一种贪心解法：从(0,0)开始，不断寻找当前节点的最大邻居，并不断迭代，时间复杂度O(n^2) 还有一种θ(n)的解法，详见作业解析

最大子数组

算法思路：元素和最大的子数组有三种情况：在左半数组，右半数组，或者跨越中点，第一和第二种情况可以用递归遍历解决，第三种情况则分为两个半边数组的组合，只要从中点出发寻找最大子数组，然后组合就可以了

时间复杂度分析：，其中线性时间为跨越中点的子数组，最终需要时间为O(NlogN)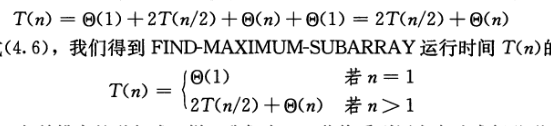

FIND-MAXIMUM-SUBARRAY(A, low， high)  
    if high== low  
        return (low, high, A[low])  
    else mid=mod((low 十 high)/2) 
        (left-low, left-high, left-sum) = FIND-MAXIMUM-SUBARRAY(A, low, mid)  
    
        (right-low, right-high, right-sum) =  FIND-MAXIMUM-SUBARRAY(A, mid+l. high)  
    
        (cross-low, cross-high, cross-sum) =  FIND-MAX-CROSSING-SUBARRAY(A, low, mid, high)  
    
    if left-sum>=right-sum and left-sum>=cross-sum  
        return (left-low, left-high, left-sum)  
    
    elseif rightr-sum>= left-sum and right-sum>= cross-sum  
        return (right-low, right-high, right-sum)  
    
    else return (cross-low, cross-high, cross-sum)

FIND-MAX-CROSSING--SUBARRAY(A, low, mid, high)  
    left-sum = -oo  
    sum=O  
    for i = mid downto low  
        sum=sum+A[i]  
        if sum> left-sum  
            left-sum = sum  
            max-left = i  
    right-sum= -oo  
    sum=O  
    for j = mid + 1 to high
        sum=sum + A[j]  
        if sum > right-sum  
            right-sum = sum  
            max-right = j  
    return (max-left, max-right, left-sum + right-sum)

选择和查找

二分搜索

普通的二分查找：

def binary_search_lcro(nums: list[int], target: int) -> int:
    """二分查找（左闭右开）"""
    # 初始化左闭右开 [0, n) ，即 i, j 分别指向数组首元素、尾元素+1
    i, j = 0, len(nums)
    # 循环，当搜索区间为空时跳出（当 i = j 时为空）
    while i < j:
        m = (i + j) // 2  # 计算中点索引 m
        if nums[m] < target:
            i = m + 1  # 此情况说明 target 在区间 [m+1, j) 中
        elif nums[m] > target:
            j = m  # 此情况说明 target 在区间 [i, m) 中
        else:
            return m  # 找到目标元素，返回其索引
    return -1  # 未找到目标元素，返回 -1

这样的二分查找只适用于不重复元素，如果有重复元素，需要寻找到左边界作为插入点，则需要进一步处理即：当找到等于目标的索引值后，进一步在左侧区间运行二分查找，直到找到最左侧的值循环完成后， i指向最左边的 target ， j指向首个小于 target 的元素，因此索引 i就是插入点。

def binary_search_insertion(nums: list[int], target: int) -> int:
    """二分查找插入点（存在重复元素）"""
    i, j = 0, len(nums) - 1  # 初始化双闭区间 [0, n-1]
    while i <= j:
        m = (i + j) // 2  # 计算中点索引 m
        if nums[m] < target:
            i = m + 1  # target 在区间 [m+1, j] 中
        elif nums[m] > target:
            j = m - 1  # target 在区间 [i, m-1] 中
        else:
            j = m - 1  # 首个小于 target 的元素在区间 [i, m-1] 中
    # 返回插入点 i
    return i

查找左边界

def binary_search_left_edge(nums: list[int], target: int) -> int:
    """二分查找最左一个 target"""
    # 等价于查找 target 的插入点
    i = binary_search_insertion(nums, target)
    # 未找到 target ，返回 -1
    if i == len(nums) or nums[i] != target:
        return -1
    # 找到 target ，返回索引 i
    return i

我们可以利用查找最左元素的函数来查找最右元素，具体方法为：将查找最右一个 target 转化为查找最左一个 target + 1。搜索结束后j指向最右一个 target ，因此返回j 即可

def binary_search_right_edge(nums: list[int], target: int) -> int:
    """二分查找最右一个 target"""
    # 转化为查找最左一个 target + 1
    i = binary_search_insertion(nums, target + 1)
    # j 指向最右一个 target ，i 指向首个大于 target 的元素
    j = i - 1
    # 未找到 target ，返回 -1
    if j == -1 or nums[j] != target:
        return -1
    # 找到 target ，返回索引 j
    return j

当数组不包含 target 时，最终 i和j

会分别指向首个大于、小于 target 的元素。

因此，可以构造一个数组中不存在的元素，用于查找左右边界。

查找最左一个 target ：可以转化为查找 target - 0.5 ，并返回指针i
查找最右一个 target ：可以转化为查找 target + 0.5 ，并返回指针j

哈希查找

Q:给定一个整数数组 nums 和一个目标元素 target ，请在数组中搜索“和”为 target 的两个元素，并返回它们的数组索引。返回任意一个解即可。

借助一个哈希表，键值对分别为数组元素和元素索引。循环遍历数组

判断数字 target - nums[i] 是否在哈希表中，若是则直接返回这两个元素的索引。
将键值对 nums[i] 和索引 i 添加进哈希表。

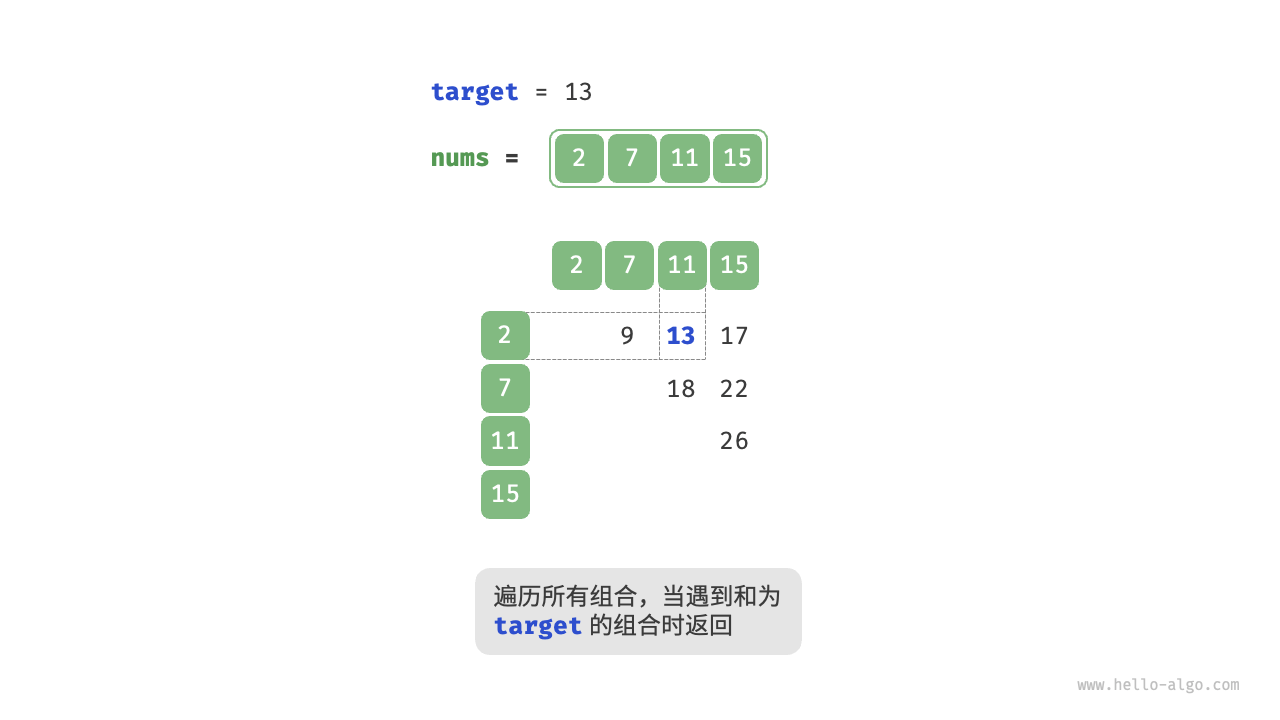
def two_sum_hash_table(nums: list[int], target: int) -> list[int]:
    """方法二：辅助哈希表"""
    # 辅助哈希表，空间复杂度 O(n)
    dic = {}
    # 单层循环，时间复杂度 O(n)
    for i in range(len(nums)):
        if target - nums[i] in dic:
            return [dic[target - nums[i]], i]
        dic[nums[i]] = i
    return []

时间复杂度O(n),由于需要维护一个额外的哈希表，因此空间复杂度为O(n)

随机查找

RANDOMIZED-SELECT (A, p, r, i)
    if p==r
        return A[p]
    q = RANDOMlZED-PARTITION(A, p, r)
    k = q-p+I
    if i == k // the pivot value is the answer
        return A[q]
    else if i<k
        return RANOOMIZED-SELECT(A, p, q-1, i)
    else return RANOOMIZED-SELECT(A, q+l, r, i-k

期望线性时间的查找

RANDOMIZED-SELECT(A, p, r, i)  
if p == r  
	return A[p]  
q = RANDOMIZED-PARTITION(A, p, r)  
k = q - p + 1  
if i == k  // the pivot value is the answer  
	return A[q]  
else if i < k  
	return RANDOMIZED-SELECT(A, p, q - 1, i)  
else return RANDOMIZED-SELECT(A, q + 1, r, i - k)

最坏运行时间为线性的中位数查找

将输入数组的 n 个元素划分为 ⌊n/5 ⌋组，每组 5 个元素，且至多只有一组由剩下的 nmod5 个元素组成。
寻找这⌈ n/5⌉ 组中每一组的中位数：首先对每组元素进行插入排序，然后确定每组有序元素的中位数。
对第 2 步中找出的「 n/5 ⌉个中位数，递归调用 SELECT 以找出其中位数 x( 如果有偶数个中位数，为了方便，约定 x 是较小的中位数）。
利用修改过的 PARTITION 版本，按中位数的中位数 x 对输入数组进行划分。让 K 比划分的低区中的元素数目多 1, 因此 x 是第 k 小的元素，并且有 n-k 个元素在划分的高区。
如果 i=k, 则返回 x 。如果 i<k, 则在低区递归调用 SELECT 来找出第 i 小的元素。如果 i>k, 则在高区递归查找第 i-k 小的元素。

在第 2 步找出的中位数中，至少有一半大千或等于中位数的中位数户。因此，在这「n/5⌉个组中，除了当 n 不能被 5 整除时产生的所含元素少于 5 的那个组和包含 x 的那个组之外，至少有一半的组中有 3 个元素大千 x 。不算这两个组，大于 x 的元素个数至少为： \(3\Bigl(\biggl\lceil\frac{1}{2}\biggl\lceil\frac{n}{5}\biggr\vert-2\Bigr)\ge\frac{3n}{10}-6\) 也至少有这个数的元素小于x

\(T(n)<={T([n/5])+T(7n/10+6)+O(n)}\)

def divide(A):
    array_num=len(A)//5
    matrix=[]
    index=0
    for i in range (array_num):
        new_array=[]
        for j in range(5):
            new_array.append(A[index])
            index+=1
        matrix.append(new_array)
    if index==len(A): return matrix
    else:
        new_array=[]
        while index<len(A):
            new_array.append(A[index])
            index+=1
        matrix.append(new_array)
    return matrix
def insertion_sort(nums):
    for i in range(1, len(nums)):
        base = nums[i]
        j = i - 1
        while j >= 0 and nums[j] > base:
            nums[j + 1] = nums[j]  
            j -= 1
        nums[j + 1] = base  
    return nums
def swap(A,i,j):
    temp=A[i]
    A[i]=A[j]
    A[j]=temp
    return A

def partition(nums, left, right,x):
    i, j = left, right
    while i < j:
        while i < j and nums[j] > x:
            j -= 1  
        while i < j and nums[i] <= x:
            i += 1  
        nums[i], nums[j] = nums[j], nums[i]
    nums[i], nums[left] = nums[left], nums[i]
    return i  

def select(A,ith):
    matrix = divide(A)#划分n/5个数组
    medium_nums=[]
    for i in range(len(matrix)):#产生中位数数组
        matrix[i]=insertion_sort(matrix[i])
        medium_nums.append(matrix[i][(len(matrix[i])-1)//2])
    medium_nums=insertion_sort(medium_nums)#对中位数数组排序
    if len(medium_nums)%2==0:
        medium=(len(medium_nums)-1)//2
    else: medium=len(medium_nums)//2#计算出中位数数组的中位数索引并向下取整
    x=medium_nums[medium]
    k=partition(A,0,len(A)-1,x)+1#划分数组
    if k==ith: return x
    elif ith<k: return select(A[0:k],ith)
    else: return select(A[k:],ith-k)

def main():
    A=[41,5,46,48,456,1,56,1448,21,84,49,11]
    for i in range(1,len(A)+1):
        print('第'+str(i)+'个元素是：')
        print(select(A,i))
main()

比较排序

决策树

任何算法都可以被视为所执行操作的决策树
内部节点表示二进制比较，分支为 True 或 False
对于比较算法，决策树是二元的
叶子代表算法终止，产生算法输出
根到叶路径表示算法在某些输入上的执行
比较排序的决策树是完全二叉树，因此高度h>=lg(叶节点数)
叶结点数是排列数量，即n!
决策树高度，或者说每条路径的长度就是时间复杂度 \[n! = \sqrt{2\pi n}\Bigl(\frac{n}{\mathrm{e}}\Bigr)^{n}\Bigl(1 + \frac{1}{12n} + \frac{1}{288n^2} + \cdots\Bigr),\] \[\ln n! = n\ln n - n +\frac{1}{2}\ln(2\pi n) + \frac{1}{12n} - \frac{1}{360n^3} + \cdots.\] 因此排序下界是nlgn

对应的，搜索算法的叶节点数为n个，因此下界是lgn

堆排序

本质上是在序列数据结构（数组）之上实现集合数据结构

二叉堆：将数组解释为完全二叉树，深度 i 处最多有 2i 个节点，除了在最大深度，所有节点均左对齐

1
2
3

left(i) = 2i + 1
right(i) = 2i + 2
parent(i) = mod(i-1/2)

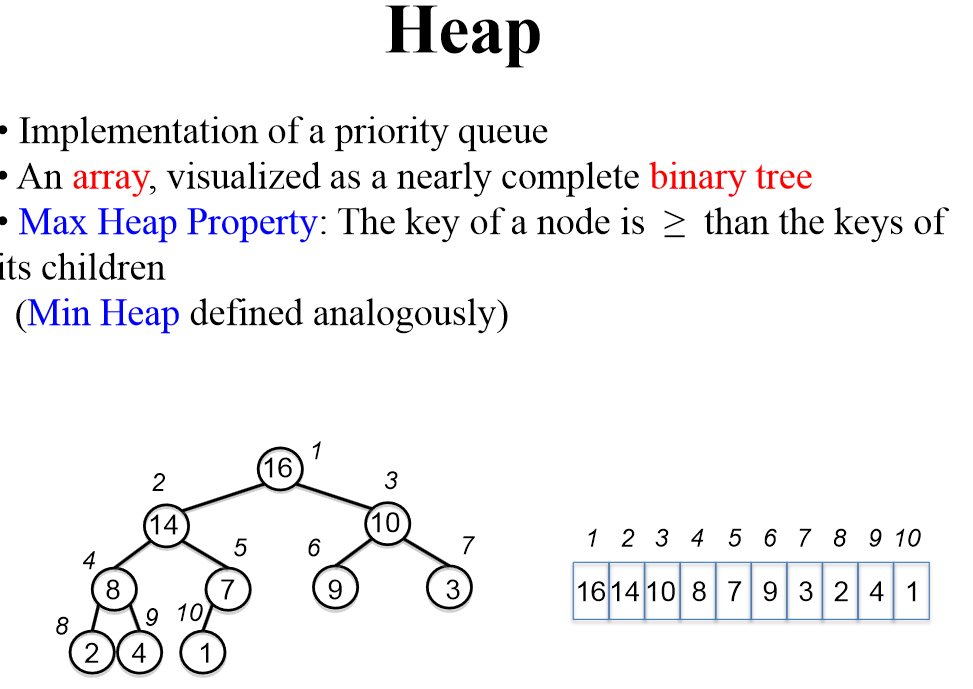
最大堆的生成

本质上是自底向上建堆，从下到上维护最大堆属性，即从倒数第二层由大索引值向顶部进行最大堆性质的维护

Max_Heapify(A,i)
    l = left(i)
    r = right(i)
    if (l <= heap-size(A) and A[l] > A[i])
        then largest = l 
    else largest = i
    if (r <= heap-size(A) and A[r] > A[largest])
        then largest = r
    if largest != i
        then exchange A[i] and A[largest]
    Max_Heapify(A, largest)

//Converts A[1…n] to a max heap
Build_Max_Heap(A):
    for i=n/2 downto 1
        do Max_Heapify(A, i)

/*
Why start at n/2?
Because elements A[n/2 + 1 … n] are all leaves of the tree
*/

时间复杂度分析

每层的时间代价等于节点数乘以节点高度 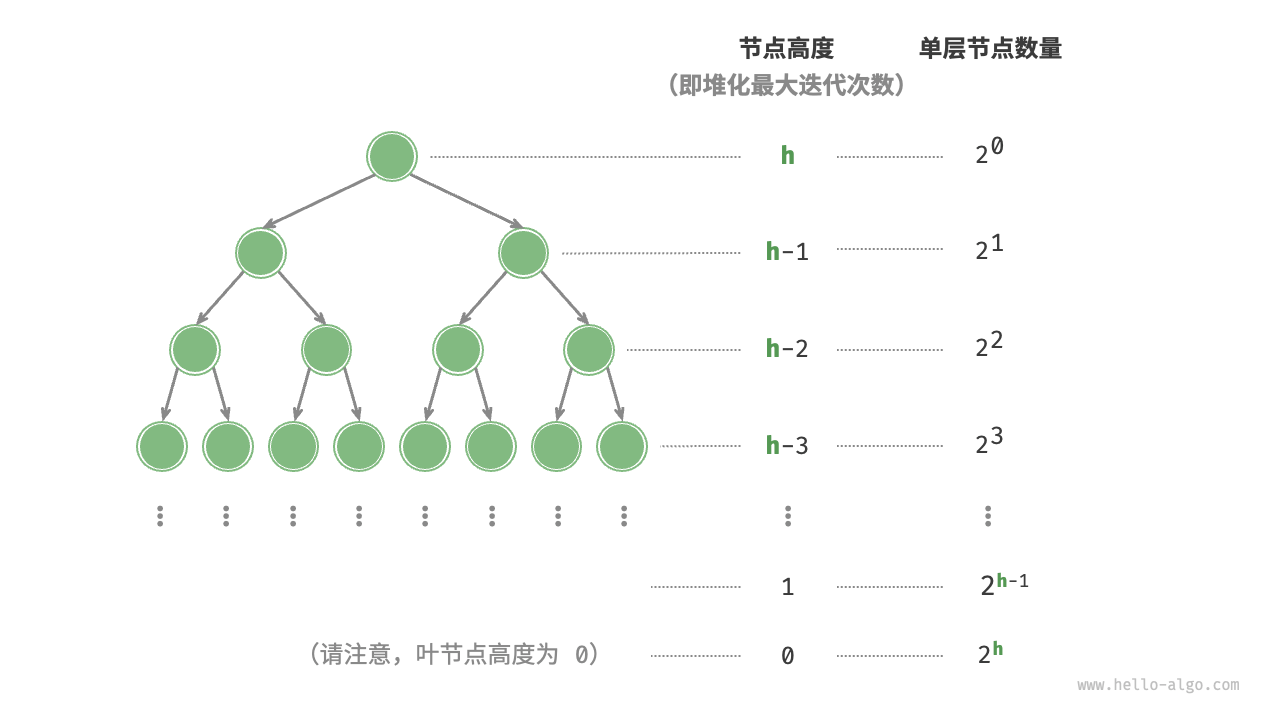\[\begin{aligned} T(h) = 2^0h + 2^1(h-1) + 2^2(h-2) + \dots + 2^{(h-1)}\times1 \newline 2T(h) - T(h) = T(h) = -2^0h + 2^1 + 2^2 + \dots + 2^{h-1} + 2^h \newline \end{aligned}\] \[\begin{aligned} T(h) & = 2 \frac{1 - 2^h}{1 - 2} - h \newline & = 2^{h+1} - h - 2 \newline & = O(2^h) \end{aligned}\] 综上得到 \[O(2^h) = O(n)\]

排序策略

Sorting Strategy:
1. 从未排序数组中构建一个堆
2. 找到最大元素 A[1]并与A[n]交换;
3. n索引处元素出堆，从顶部节点开始维护最大堆属性
4. 顶部节点开始和比它大的最大子节点交换，直到叶节点

top-k问题

基于堆更加高效地解决 Top-K 问题

初始化一个最小堆
前k个元素入堆
对之后的元素，如果有比堆顶大的元素，则堆顶出堆，该元素入堆
最后得到top-k元素组成的堆

时间复杂度是nlgk，不超过nlgn

动态规划和二分搜索树

实例——机场的动态规划：

机场维护一个跑道队列
未来的着陆预定登记到队列
一架飞机着陆后就出队
有新的请求且需要着陆时间t时，如果k时间内没有其他需求，则需求t时间的请求入队(k可以实时改变)

init: R = [ ]
req(t): if t < now: return "error"
for i in range (len(R)):
    if abs(t-R[i]) < k: return "error"
R.append(t)
R = sorted(R)
land: t = R[0]
if (t != now) return error
R = R[1: ] (drop R[0] from R)

Goal: Run this system efficiently in O(lg n) time 常见数据结构运行时间分析

排序链表
- 添加元素并排序需要Θ(nlgn)时间。但是,可以找到插入新时间/航班的位置而不需要添加并排序,但是插入需Θ(n)时间。一旦找到插入位置,k分钟检查可以在O(1)时间内完成。

排序数组
- 可以使用二分搜索在O(lg n)时间内找到插入位置。使用二分搜索,找到插入索引i,即大于或等于t的最小元素。然后将R[i]和R[i-1]与t进行比较。然而,实际插入需要移位元素,需Θ(n)时间。

未排序链表/数组
- k分钟检查需要O(n)时间。

最小堆
- 可以在O(lg n)时间内插入。但是,k分钟检查仍需O(n)时间。

字典或Python集合
- 插入需要O(1)时间。k分钟检查需要Ω(n)时间

BST的定义：每个节点都有一个key,左节点的key小于等于父节点，右节点的key大于等于父节点

所有操作都是O(h)即O(lgn)

动态规划中需要找到比一个值大的值中的最小值

next-larger(x) # x is a node in the BST
if right child not NIL, return minimum(right)
else y = parent(x)
while y not NIL and x = right(y)
    x = y; y = parent(y)
return(y);

子问题：如何计算小于等于时间t内着陆的飞机数量

1 2	1. 遍历树找到目标时间 2. 从左子树开始遍历，把左侧节点的数量加一则是当前节点的排名，排名则是问题的答案

搜索二叉树可以使用set或者sequence两种数据结构

set:遍历顺序由key的顺序决定

sequence:数组索引就是遍历顺序

查找第i大的节点(sequence)

1. 查找当前节点的排序rank
2. 如果rank < i在右子树寻找排名i-rank的节点
3. 如果rank > i在左子树递归寻找
4. 如果等于，则找到了目标

也可以对每个节点维护一个size属性，用左子树的size确认排名
搜索二叉树插入节点很容易实现，但删除节点，如果是有子树的节点，就需要把左子树的最大值或者右子树的最小值与其交换后删除
二叉树的中序遍历正好就是一个排序数组

平衡二叉搜索树AVL

• 在动态操作下保持 O(log n) 高度的二叉树称为平衡二叉树 – 有许多平衡方案（红黑树、八字树、2-3 树……） – 第一个提出的平衡方案是 AVL 树 树的旋转 • 定理：O(n) 次旋转可以将二叉树转换为具有相同遍历顺序的任何其他二叉树。 • 证明：按照遍历顺序重复执行最后可能的右旋转；结果树是规范链。每次旋转都会使最后一个节点的深度增加 1。最后一个节点的深度最多为 n − 1，因此最多执行 n − 1 次旋转，就可以将输入树旋转为目标树。

平衡 AVL 树保持高度平衡（也称为 AVL 属性）

如果一个节点的左右子树的高度最多相差 1，则该节点是高度平衡的
节点的倾斜为其右子树的高度减去左子树的高度
如果节点的倾斜度为 −1、0 或 1，则该节点是高度平衡的

平衡的维持 每次对树的修改最多导致左右子树高度相差2，如果相差2，一次旋转就可以重新平衡树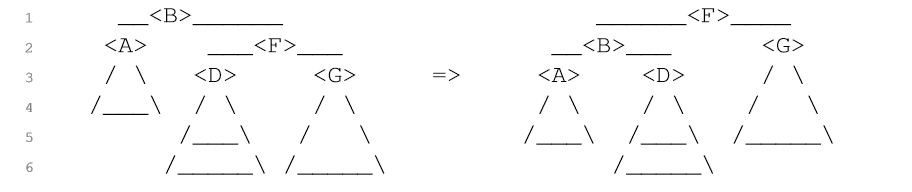

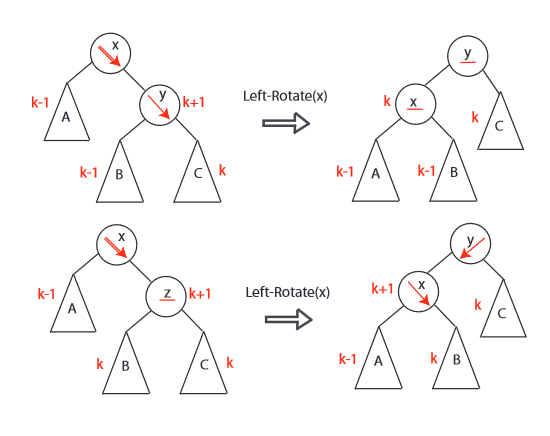
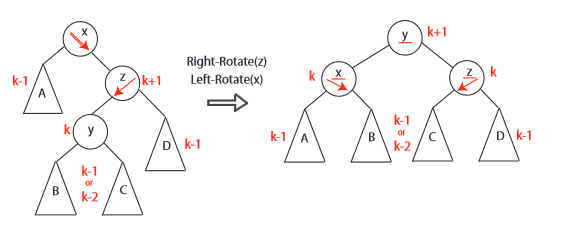
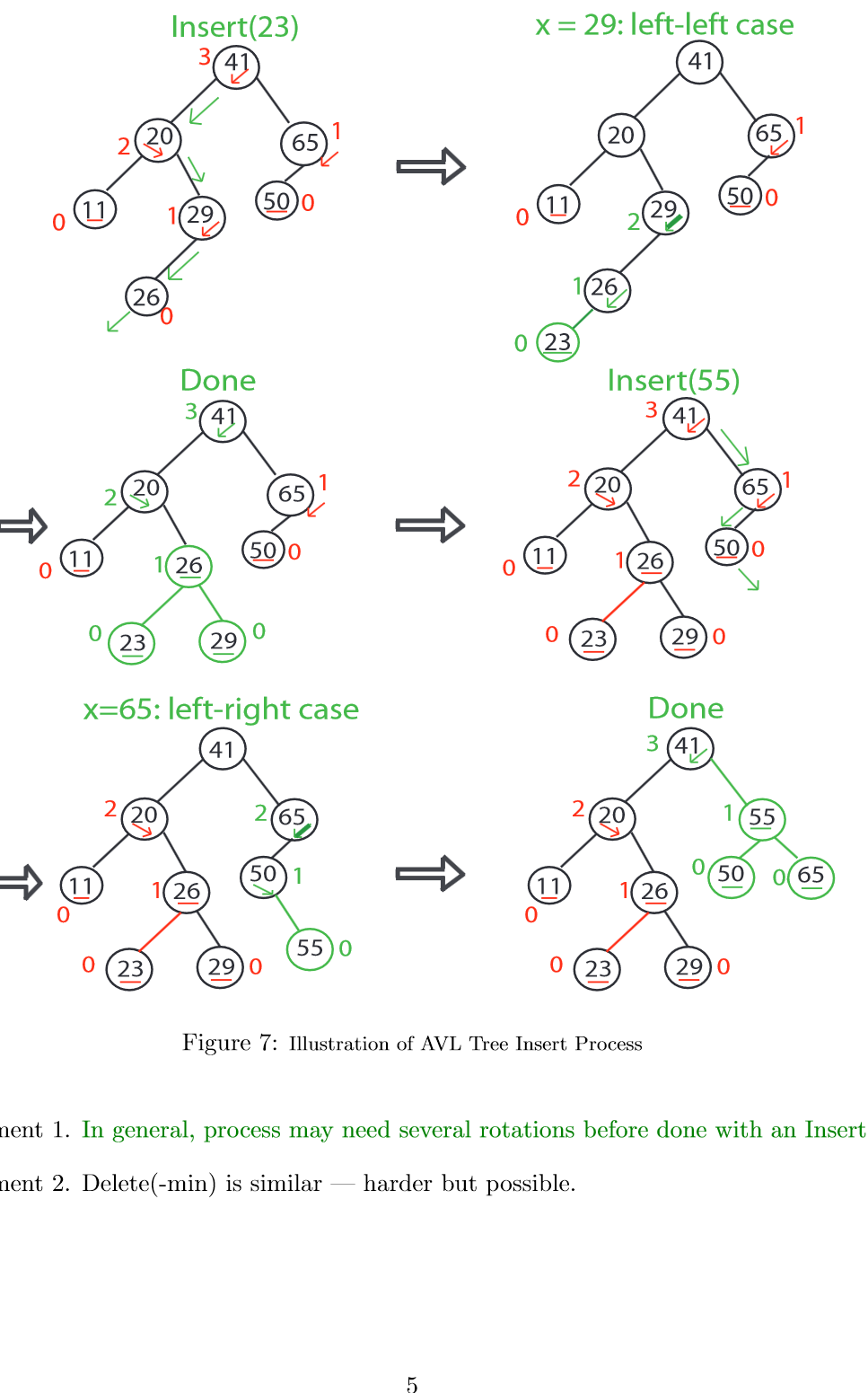
AVL 树通过在每个节点存储额外的高度信息,并在每个节点做平衡操作来保持平衡。其平衡调整原则如下:

如果左右子树高度相差大于 1,进行旋转操作调整;
进行左旋转的情况:左子树高度 - 右子树高度 > 1,即左子树比右子树高(左重),需要右旋;
进行右旋转的情况:右子树高度 - 左子树高度 > 1,即右子树比左子树高(右重),需要左旋;
旋转后更新节点的高度信息。
每进行一次插入或删除节点后,从该节点开始向上遍历,如果发现任一节点的左右子树高度差大于 1,则在该节点进行旋转操作,调整树的平衡。由于树的高度最高为lgn，所以logn时间内就可以完成增删节点的操作 高度属性的维护 必须确保每个节点的height属性可以通过对height属性的一个O(1)操作完成，这样维护height就不会改变动态操作的复杂度

/* 获取节点高度 */
int height(TreeNode *node) {
    // 空节点高度为 -1 ，叶节点高度为 0
    return node == nullptr ? -1 : node->height;
}

/* 更新节点高度 */
void updateHeight(TreeNode *node) {
    // 节点高度等于最高子树高度 + 1
    node->height = max(height(node->left), height(node->right)) + 1;
}

/* 获取平衡因子 */
int balanceFactor(TreeNode *node) {
    // 空节点平衡因子为 0
    if (node == nullptr)
        return 0;
    // 节点平衡因子 = 左子树高度 - 右子树高度
    return height(node->left) - height(node->right);
}

旋转的实现


/* 右旋操作 */
TreeNode *rightRotate(TreeNode *node) {
    TreeNode *child = node->left;
    TreeNode *grandChild = child->right;
    // 以 child 为原点，将 node 向右旋转
    child->right = node;
    node->left = grandChild;
    // 更新节点高度
    updateHeight(node);
    updateHeight(child);
    // 返回旋转后子树的根节点
    return child;
}

/* 左旋操作 */
TreeNode *leftRotate(TreeNode *node) {
    TreeNode *child = node->right;
    TreeNode *grandChild = child->left;
    // 以 child 为原点，将 node 向左旋转
    child->left = node;
    node->right = grandChild;
    // 更新节点高度
    updateHeight(node);
    updateHeight(child);
    // 返回旋转后子树的根节点
    return child;
}

一共有四种需要平衡的情况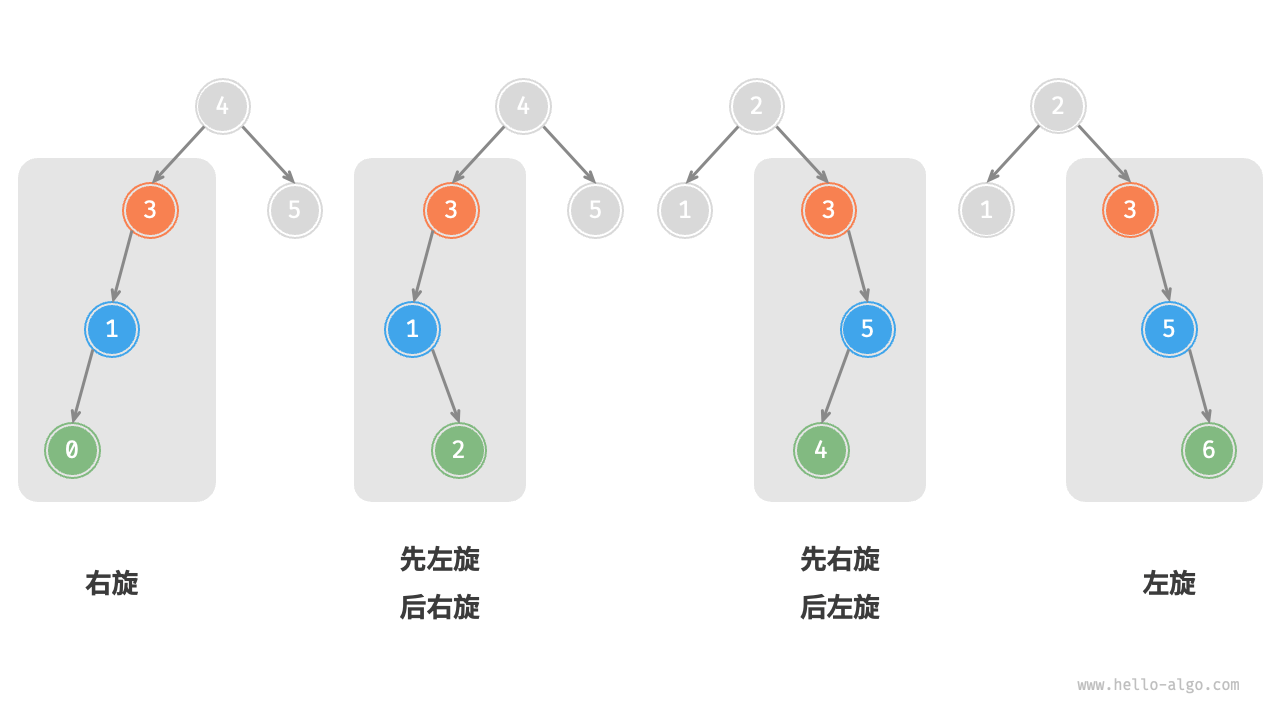

失衡节点的平衡因子	子节点的平衡因子	应采用的旋转方法
>1（即左偏树）	>=0	右旋
>1（即左偏树）	<0	先左旋后右旋
<-1（即右偏树）	<=0	左旋
<-1（即右偏树）	>0	先右旋后左旋

数据结构的选取 • Set AVL trees achieve O(lg n) time for all set operations, except O(n log n) time for build and O(n) time for iter • Sequence AVL trees achieve O(lg n) time for all sequence operations, except O(n) time for build and iter 插入和删除 此外，插入节点和删除节点在搜索二叉树基础上，需要分别自底向上和自上向下进行恢复平衡的操作

哈希

哈希有可能产生碰撞，需要特定处理或者数据结构，检索元素时间最后会由负载因数(n/m)决定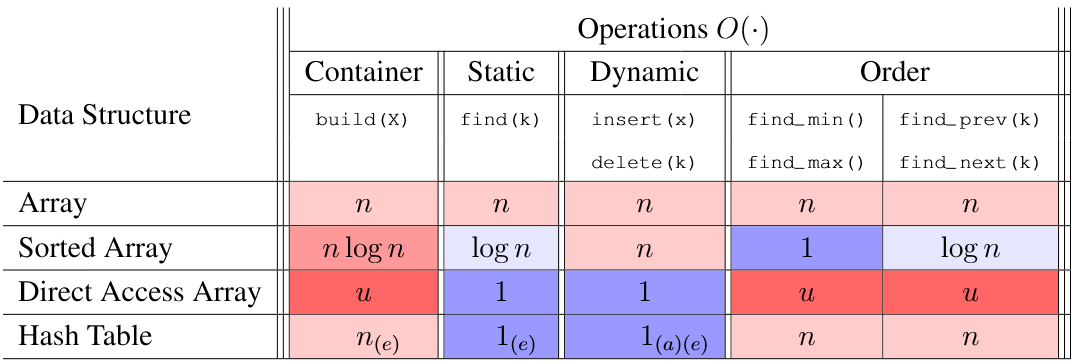一般有链表和开放寻址两种方式解决碰撞

链表期望的查找时间，θ(1+α)，1是哈希函数用时，阿尔法则是查找具体链表需要的时间（链表的期望长度）
开放寻址

哈希函数

常见的哈希函数

h(k) = k mod m（m是素数，慢)
h(k) = [(a · k) mod 2w] >> (w − r)(where a is random, k is w bits, and m = 2r.且需要a处于2^(w-1)和2w之间，且不靠近端点)
h(k) = [(ak + b) mod p] mod m where a and b are random ∈ {0, 1, . . . p − 1}, and p is a large prime (> |U|).(了解即可,6.046内容)

哈希的优化

rehash

Θ(n + m) time = Θ(n) if m = Θ(n)

shrink

当n到达m/4时，收缩到n/2

利用哈希的字符串匹配算法

Karp-Rabin Algorithm

Rabin-Karp算法是一种字符串匹配算法,利用滚动哈希技术实现。其基本思想是:

对文本和模式分别计算哈希值;
滚动文本,每次比较文本窗口和模式的哈希值;
如果哈希值相同,则进行字符匹配确认;
如果不相同,则可以直接跳到下一位置。

• Compare h(s) == h(t[i : i + len(s)])
• If hash values match, likely so do strings
– can check s == t[i : i + len(s)] to be sure ∼ cost O(|s|)
– if yes, found match — done
– if no, happened with probability < 1/|s|
= expected cost is O(1) per i.
⇒
• need suitable hash function.
• expected time = O(|s| + |t| · cost(h)).
– naively h(x) costs |x|
– we’ll achieve O(1)!
– idea: t[i : i + len(s)] ≈ t[i + 1 : i + 1 + len(s)]

rolling hash

Rolling Hash ADT

Maintain string x subject to

r(): reasonable hash function h(x) on string x
r.append(c): add letter c to end of string x
r.skip(c): remove front letter from string x, assuming it is

伪代码

for c in s: rs.append(c)
for c in t[:len(s)]: rt.append(c)
if rs() == rt(): ...
//This first block of code is O( s )
for i in range(len(s), len(t)):
rt.skip(t[i-len(s)])
rt.append(t[i])
if rs() == rt(): ...
//The second block of code is O(|t|) + O(# matches − |s|) to verify.

开放寻址

哈希时需要引入哈希次数i，持续哈希直到找到空槽插入

for i in xrange(m):
    if T [h(k, i)] is None: #empty slot
        T [h(k, i)] = (k, v) #store item
        return
raise ‘full'

查找

for i in xrange(m):
    if T [h(k, i)] is None: #empty slot?
        return None #end of “chain”
    elif T [h(k, i)][∅] == k: #matching key
        return T [h(k, i)] #return item
    return None ˙ #exhausted table

删除

由于防止查找操作误判，需要特定的删除标志，把待删除函数设置为已删除，让插入视为None,查找视为存在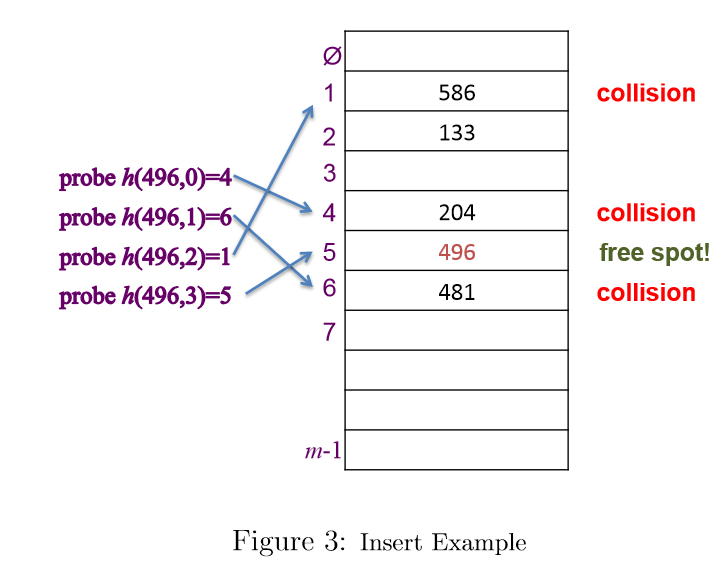

优化

问题：可能出现簇现象，某些元素连续聚集于一处，导致查找操作耗时较高

eg.线性哈希h(k, i) = (h′(k) +i)

更好的解决方案：h(k, i) =(h1(k) +i·h2(k)) mod m where h1(k) and h2(k) are two ordinary hash func-tions.

性能

第一次查找成功的概率p=m-n/m

第二次概率为m-n/m-1大于p

由此类推，成功概率至少为p

1/p=1/1-α

所以期望时间为O(1/(1 − α))

与链表的比较

优点：更有效地利用空间，不需要储存指针

缺点：链表对哈希函数和负载值的要求更低，开放寻址高负载时性能大降，且无法有大于一的α

安全领域的哈希

哈希在加密上应用广泛，例如：

加密密码，存储密码的哈希码来防止泄露的危害
文件完整性校验，利用哈希来给出文件几乎唯一的哈希值来防止对文件的暗中篡改，也用于git之类的版本控制软件
数字签名，用私钥加密数据，其他人可以用公钥检验，来确保发信者身份正规详细可见Sysadmin decal笔记

6.006没涉及的其他排序

冒泡排序

「冒泡排序 bubble sort」通过连续地比较与交换相邻元素实现排序。这个过程就像气泡从底部升到顶部一样，因此得名冒泡排序。设数组的长度为n，冒泡排序的步骤

首先，对 n 个元素执行“冒泡”，将数组的最大元素交换至正确位置，
接下来，对剩余n-1个元素执行“冒泡”，将第二大元素交换至正确位置。
以此类推，经过n-轮“冒泡”后，前n-1 大的元素都被交换至正确位置。
仅剩的一个元素必定是最小元素，无须排序，因此数组排序完成。

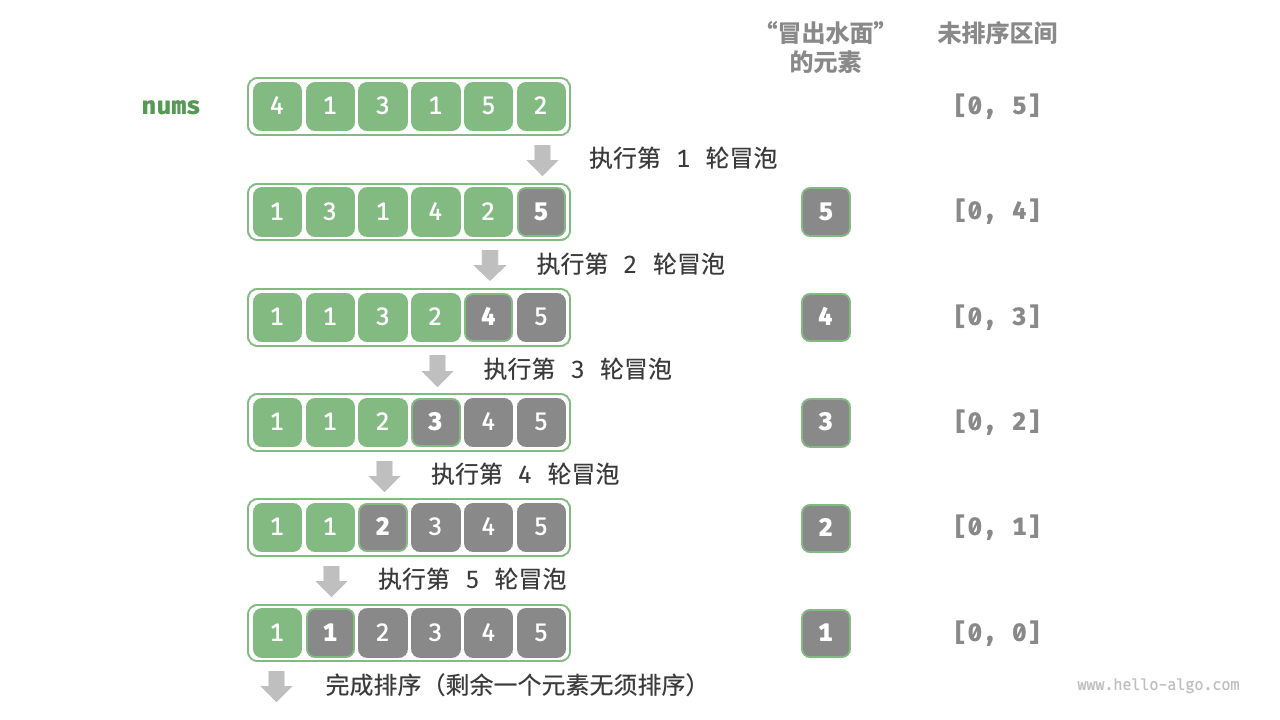
def bubble_sort(nums: list[int]):
    """冒泡排序"""
    n = len(nums)
    # 外循环：未排序区间为 [0, i]
    for i in range(n - 1, 0, -1):
        # 内循环：将未排序区间 [0, i] 中的最大元素交换至该区间的最右端
        for j in range(i):
            if nums[j] > nums[j + 1]:
                # 交换 nums[j] 与 nums[j + 1]
                nums[j], nums[j + 1] = nums[j + 1], nums[j]

性能和特性：

最差和平均都是O(n^2)，但比较适合数组有一定秩序性的时候
原地稳定排序

快速排序

「快速排序 quick sort」是一种基于分治策略的排序算法，核心操作是“哨兵划分”，其目标是：选择数组中的某个元素作为“基准数”，将所有小于基准数的元素移到其左侧，而大于基准数的元素移到其右侧。

选取数组最左端元素作为基准数，初始化两个指针 i 和 j 分别指向数组的两端。
设置一个循环，在每轮中使用 i（j）分别寻找第一个比基准数大（小）的元素，然后交换这两个元素。
循环执行步骤 2. ，直到 i 和 j 相遇时停止，最后将基准数交换至两个子数组的分界线。

伪代码：

PARTITION(A, p, r)
 i =RANOOM(p, r)
 exchange A[r] with A[i]
 x = A[r]
 i = p —1
 for j=p to r-1
  if A[j]<=x
  i = i + 1
  exchange A[i] with A[j]
 exchange A[i+ l] with A[r]
 return i + 1

QUICKSORT(A, p, r)
if p<r
 q = PARTITION(A, p, r)
 QUICKSORT(A, p, q-1)
 QUICKSORT(A, q+ 1, r)

python实现:

def partition(self, nums: list[int], left: int, right: int) -> int:
    """哨兵划分"""
    # 以 nums[left] 作为基准数
    i, j = left, right
    while i < j:
        while i < j and nums[j] >= nums[left]:
            j -= 1  # 从右向左找首个小于基准数的元素
        while i < j and nums[i] <= nums[left]:
            i += 1  # 从左向右找首个大于基准数的元素
        # 元素交换
        nums[i], nums[j] = nums[j], nums[i]
    # 将基准数交换至两子数组的分界线
    nums[i], nums[left] = nums[left], nums[i]
    return i  # 返回基准数的索引

def quick_sort(self, nums: list[int], left: int, right: int):
    """快速排序"""
    # 子数组长度为 1 时终止递归
    if left >= right:
        return
    # 哨兵划分
    pivot = self.partition(nums, left, right)
    # 递归左子数组、右子数组
    self.quick_sort(nums, left, pivot - 1)
    self.quick_sort(nums, pivot + 1, right)

优化：

对主元选取可以用随机数或者取样一些元素选取中位数来实现稳定的nlgn性能
对相等元素较多的数组，可以进行三路快排，只需要递归排序不等于主元的两路
尾递归优化,在每轮哨兵排序完成后，比较两个子数组的长度，仅对较短的子数组进行递归。由于较短子数组的长度不会超过n/2 ，因此这种方法能确保递归深度不超过lgn ，从而将最差空间复杂度优化至lgn。

def quick_sort(self, nums: list[int], left: int, right: int):
    """快速排序（尾递归优化）"""
    # 子数组长度为 1 时终止
    while left < right:
        # 哨兵划分操作
        pivot = self.partition(nums, left, right)
        # 对两个子数组中较短的那个执行快排
        if pivot - left < right - pivot:
            self.quick_sort(nums, left, pivot - 1)  # 递归排序左子数组
            left = pivot + 1  # 剩余未排序区间为 [pivot + 1, right]
        else:
            self.quick_sort(nums, pivot + 1, right)  # 递归排序右子数组
            right = pivot - 1  # 剩余未排序区间为 [left, pivot - 1]

堆排序

def sift_down(nums: list[int], n: int, i: int):
    """堆的长度为 n ，从节点 i 开始，从顶至底堆化"""
    while True:
        # 判断节点 i, l, r 中值最大的节点，记为 ma
        l = 2 * i + 1
        r = 2 * i + 2
        ma = i
        if l < n and nums[l] > nums[ma]:
            ma = l
        if r < n and nums[r] > nums[ma]:
            ma = r
        # 若节点 i 最大或索引 l, r 越界，则无须继续堆化，跳出
        if ma == i:
            break
        # 交换两节点
        nums[i], nums[ma] = nums[ma], nums[i]
        # 循环向下堆化
        i = ma

def heap_sort(nums: list[int]):
    """堆排序"""
    # 建堆操作：堆化除叶节点以外的其他所有节点
    for i in range(len(nums) // 2 - 1, -1, -1):
        sift_down(nums, len(nums), i)
    # 从堆中提取最大元素，循环 n-1 轮
    for i in range(len(nums) - 1, 0, -1):
        # 交换根节点与最右叶节点（即交换首元素与尾元素）
        nums[0], nums[i] = nums[i], nums[0]
        # 以根节点为起点，从顶至底进行堆化
        sift_down(nums, i, 0)

性质：nlgn,原地非稳定

计数排序

遍历数组，找出数组中的最大数字，记为，然后创建一个长度为- 的辅助数组 counter 。
借助 counter 统计 nums 中各数字的出现次数，其中 counter[num] 对应数字 num 的出现次数。统计方法很简单，只需遍历 nums（设当前数字为 num），每轮将 counter[num] 增加即可。
由于 counter 的各个索引天然有序，因此相当于所有数字已经被排序好了。接下来，我们遍历 counter ，根据各数字的出现次数，将它们按从小到大的顺序填入 nums 即可。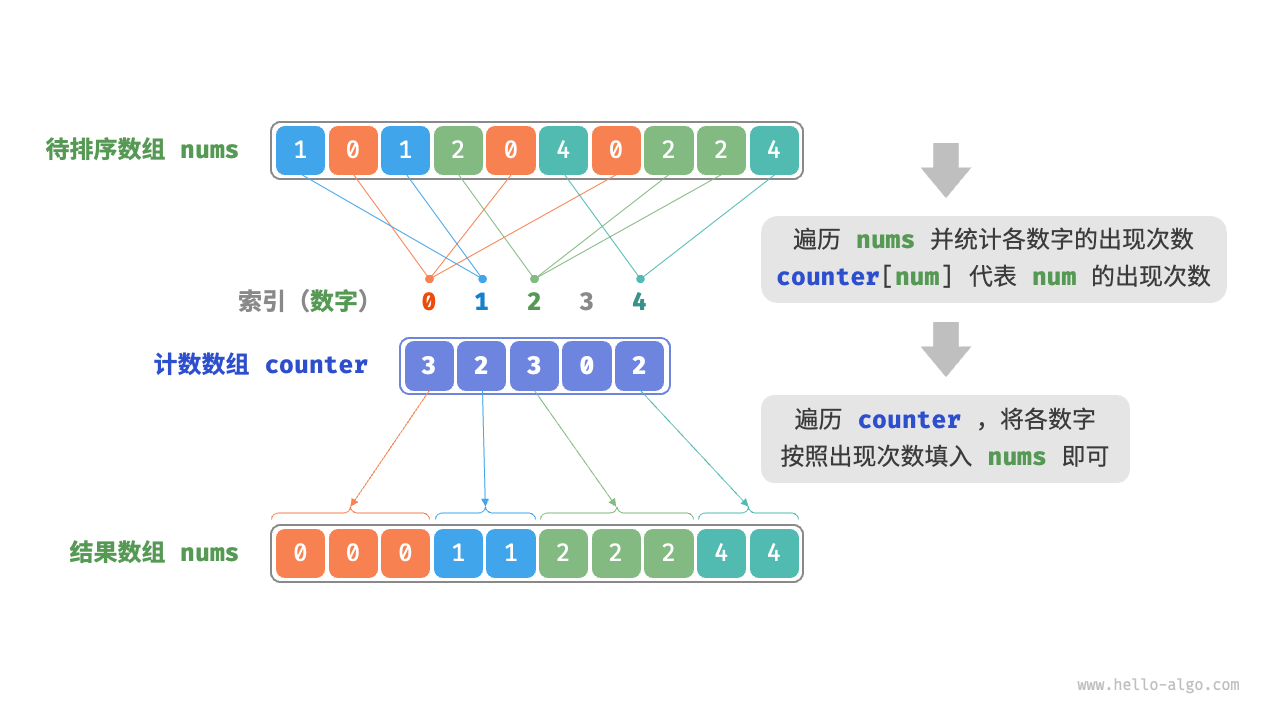

COUNTlNG-SORT(A, B, k)
let C[O .. k] be a new array
for i=O to k
 C[i] = O
for j = 1 to A. length
 C[A[j]]=C[A[j]J+ 1
//C[i] now contains the number of elements equal to i.
for i=1 to k
 C[i]=C[i]+C[i-1]
//C[i] now contains the number of elements less than or equal to i.
for j = A. length downto 1
 B[C[A[j]J]=A[j]
 C[A[j]]=C[A[j]]-1

def counting_sort(nums: list[int]):
    """计数排序"""
    # 完整实现，可排序对象，并且是稳定排序
    # 1. 统计数组最大元素 m
    m = max(nums)
    # 2. 统计各数字的出现次数
    # counter[num] 代表 num 的出现次数
    counter = [0] * (m + 1)
    for num in nums:
        counter[num] += 1
    # 3. 求 counter 的前缀和，将“出现次数”转换为“尾索引”
    # 即 counter[num]-1 是 num 在 res 中最后一次出现的索引
    for i in range(m):
        counter[i + 1] += counter[i]
    # 4. 倒序遍历 nums ，将各元素填入结果数组 res
    # 初始化数组 res 用于记录结果
    n = len(nums)
    res = [0] * n
    for i in range(n - 1, -1, -1):
        num = nums[i]
        res[counter[num] - 1] = num  # 将 num 放置到对应索引处
        counter[num] -= 1  # 令前缀和自减 1 ，得到下次放置 num 的索引
    # 使用结果数组 res 覆盖原数组 nums
    for i in range(n):
        nums[i] = res[i]

特性：虽然是线性时间O(n+m)，实际上时间复杂收到输入数据大小范围的影响,不能直接支持负数，需要将负数数组转换成非负数的排序,非原地稳定排序，空间也是O(n+m)

基数排序

假设数字的最低位是第1位，最高位是第8位，基数排序的流程:

初始化位数`k=1
对学号的第k位执行“计数排序”。完成后，数据会根据第k 位从小到大排序。
将k增加，然后返回步骤 2. 继续迭代，直到所有位都排序完成后结束。

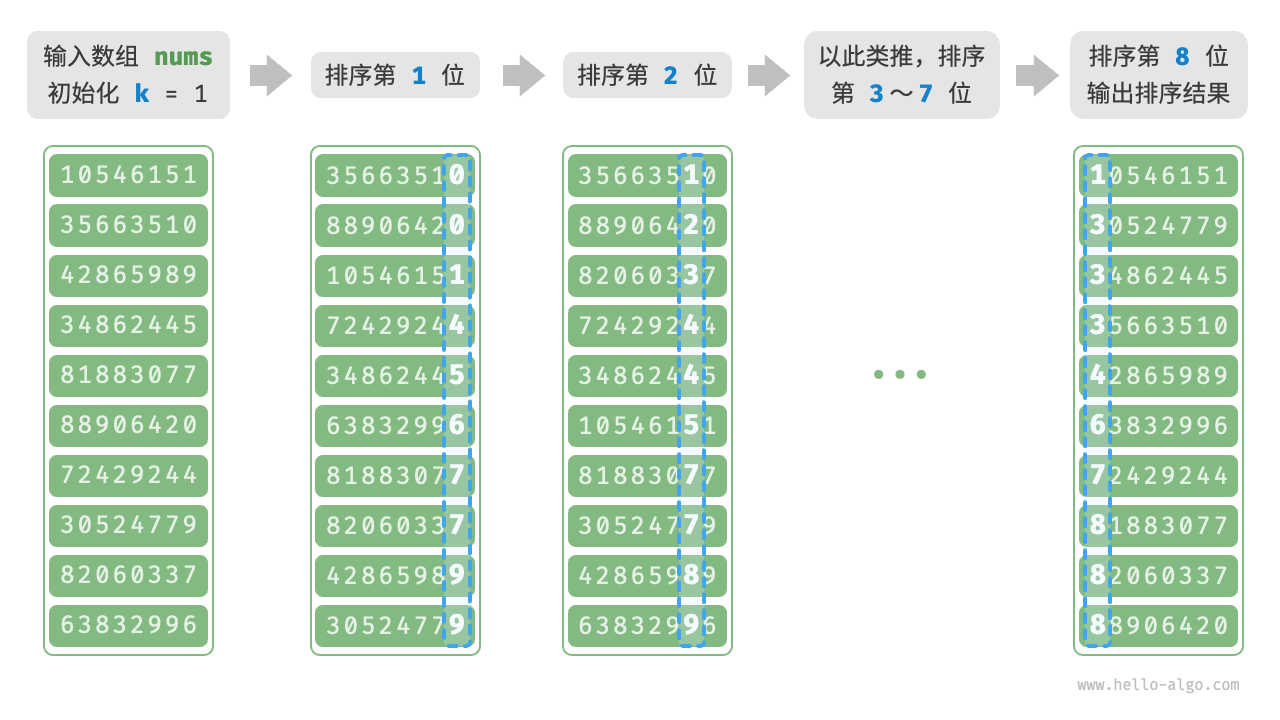获取第k位数的方法： \[x_k = \lfloor\frac{x}{d^{k-1}}\rfloor \bmod d\]

def digit(num: int, exp: int) -> int:
    """获取元素 num 的第 k 位，其中 exp = 10^(k-1)"""
    # 传入 exp 而非 k 可以避免在此重复执行昂贵的次方计算
    return (num // exp) % 10

def counting_sort_digit(nums: list[int], exp: int):
    """计数排序（根据 nums 第 k 位排序）"""
    # 十进制的位范围为 0~9 ，因此需要长度为 10 的桶
    counter = [0] * 10
    n = len(nums)
    # 统计 0~9 各数字的出现次数
    for i in range(n):
        d = digit(nums[i], exp)  # 获取 nums[i] 第 k 位，记为 d
        counter[d] += 1  # 统计数字 d 的出现次数
    # 求前缀和，将“出现个数”转换为“数组索引”
    for i in range(1, 10):
        counter[i] += counter[i - 1]
    # 倒序遍历，根据桶内统计结果，将各元素填入 res
    res = [0] * n
    for i in range(n - 1, -1, -1):
        d = digit(nums[i], exp)
        j = counter[d] - 1  # 获取 d 在数组中的索引 j
        res[j] = nums[i]  # 将当前元素填入索引 j
        counter[d] -= 1  # 将 d 的数量减 1
    # 使用结果覆盖原数组 nums
    for i in range(n):
        nums[i] = res[i]

def radix_sort(nums: list[int]):
    """基数排序"""
    # 获取数组的最大元素，用于判断最大位数
    m = max(nums)
    # 按照从低位到高位的顺序遍历
    exp = 1
    while exp <= m:
        # 对数组元素的第 k 位执行计数排序
        # k = 1 -> exp = 1
        # k = 2 -> exp = 10
        # 即 exp = 10^(k-1)
        counting_sort_digit(nums, exp)
        exp *= 10

特性： - 时间复杂度O(k(n+d))，k是位数，d是进制,d会决定计数排序需要的数组长度，k决定进行几次计数排序 - 空间复杂度O(n+d),稳定排序(从低到高排序)

桶排序

初始化 k 个桶，将n个元素分配到k个桶中
对每个桶分别执行排序
按照桶的从小到大的顺序，合并结果

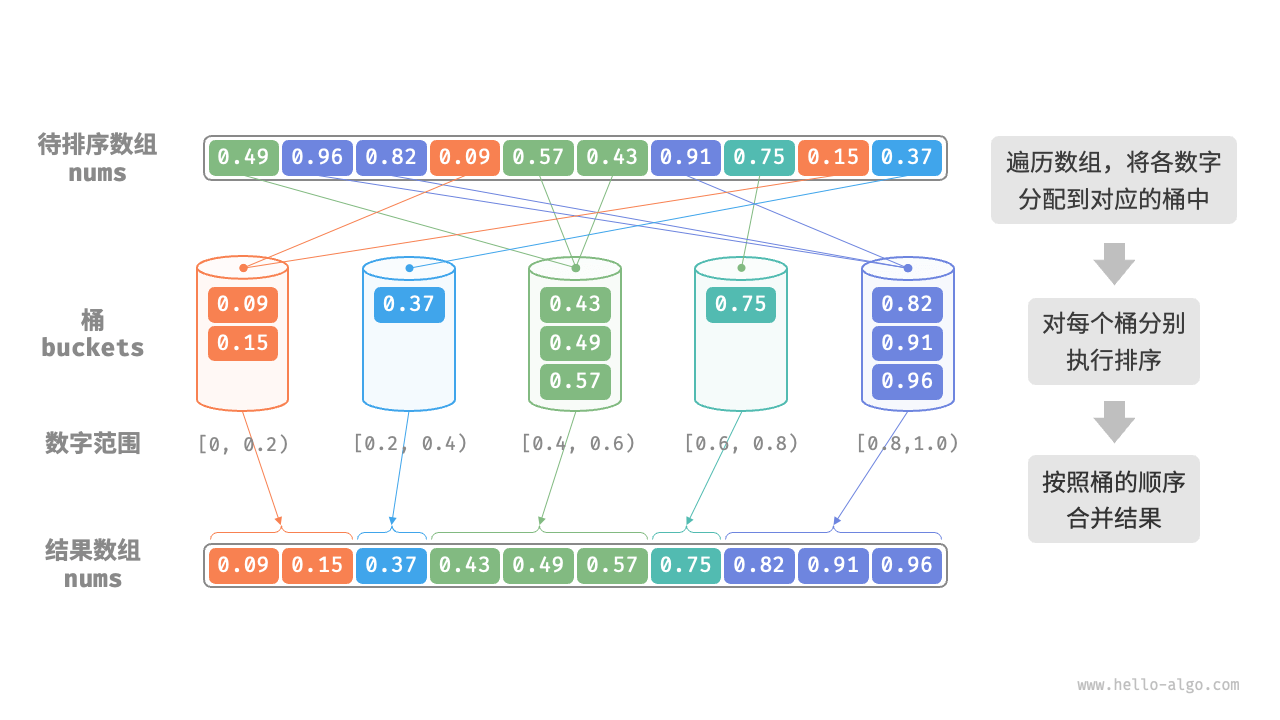
def bucket_sort(nums: list[float]):
    """桶排序"""
    # 初始化 k = n/2 个桶，预期向每个桶分配 2 个元素
    k = len(nums) // 2
    buckets = [[] for _ in range(k)]
    # 1. 将数组元素分配到各个桶中
    for num in nums:
        # 输入数据范围 [0, 1)，使用 num * k 映射到索引范围 [0, k-1]
        i = int(num * k)
        # 将 num 添加进桶 i
        buckets[i].append(num)
    # 2. 对各个桶执行排序
    for bucket in buckets:
        # 使用内置排序函数，也可以替换成其他排序算法
        bucket.sort()
    # 3. 遍历桶合并结果
    i = 0
    for bucket in buckets:
        for num in bucket:
            nums[i] = num
            i += 1

特性：

时间复杂度O(n+k) ：假设元素在各个桶内平均分布，那么每个桶内的元素数量为n/k 。假设排序单个桶使用(n/k)*lg(n/k)时间，则排序所有桶使用n*lg(n/k)时间。当桶数量k比较大时，时间复杂度则趋向于O(n) 。合并结果时需要遍历所有桶和元素，花费O(n+k)时间。在最坏情况下，所有数据被分配到一个桶中，且排序该桶使用O(n^2)时间。
空间复杂度O(n+k)
非原地排序：需要借助k个桶和总共n 个元素的额外空间。
桶排序是否稳定取决于排序桶内元素的算法是否稳定。

改良：平均分配可以对较大的桶递归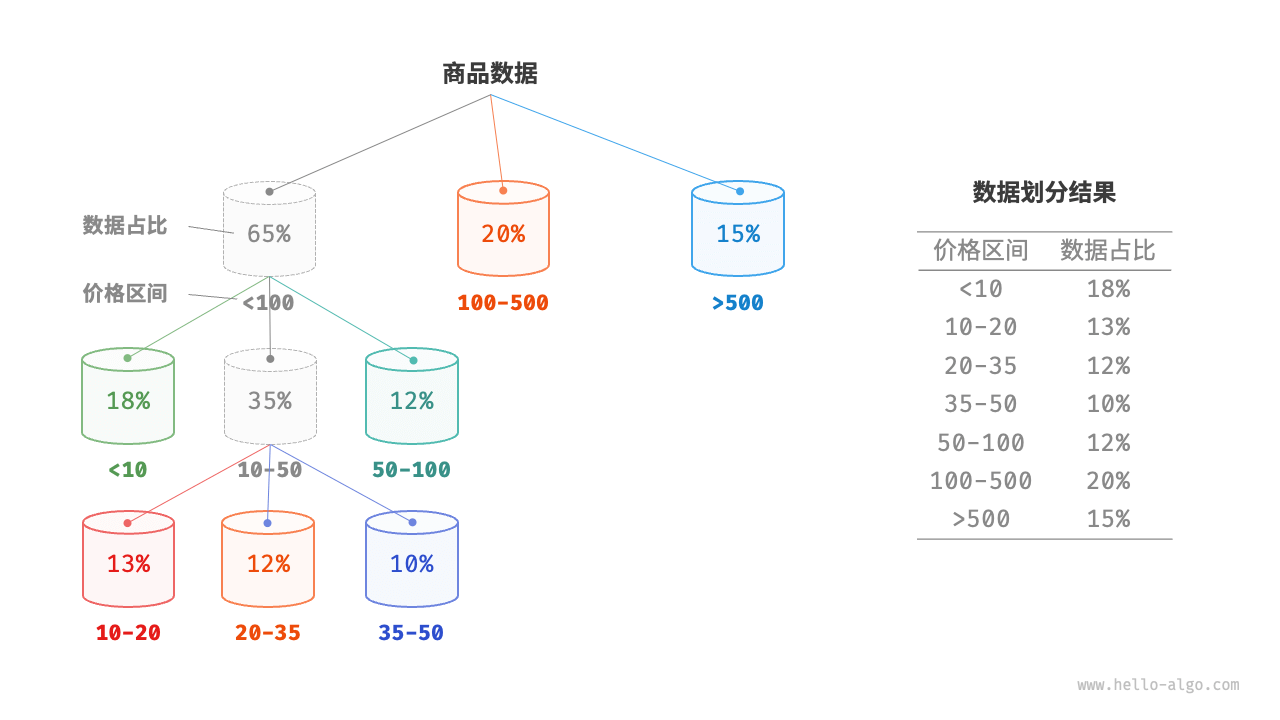或者根据概率正态分布划分桶

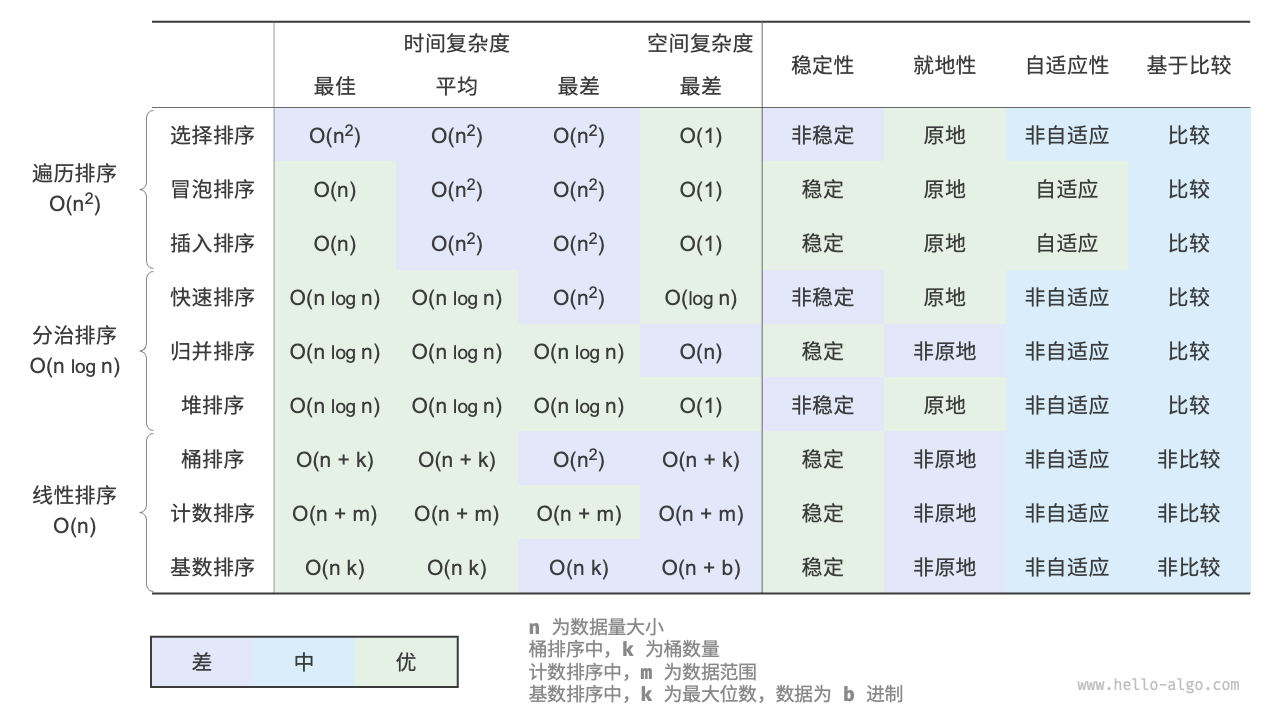
总结

数值运算

Catalan numbers

Set P of balanced parentheses strings(平衡括号字符串) are recursively defined as • λ ∈ P (λ is empty string) • If α, β ∈ P , then (α)β ∈ P Cn: number of balanced parentheses strings with exactly n pairs of parentheses 也等于n+1个叶节点构成满二叉树的形状个数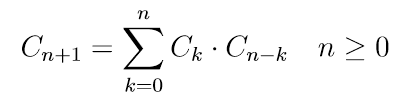

# 打印前 n 个卡特兰数
ans, n = 1, 20
print("1:" + str(ans))
for i in range(2, n + 1):
    ans = ans * (4 * i - 2) // (i + 1)
    print(str(i) + ":" + str(ans))

Newton’s Method牛顿迭代法

\[ x_{i+1} = x_{i} - \frac{f(x_{i})}{f'(x_{i})} \]

高精度乘法

Multiplying two n-digit numbers (radix r = 2, 10) 0 ≤ x, y < rn x1 = high half;x0 = low half \[ x = x_{1} \cdot r^{\frac{n}{2}} + x_{0} \] \[ y = y_{1} \cdot r^{\frac{n}{2}} + y_{0} \] \[ z = x · y = x_1y_1 · r^n + (x_0 · y_1 + x_1 · y_0)r^{n/2} + x_0 · y_0 \]

θ(n^2) time

Schönhage-Strassen算法是一种快速整数乘法算法,由Arnold Schönhage和Volker Strassen在1971年提出。它比传统的乘法算法要快得多,其时间复杂度为O(n log n log log n)。
Schönhage-Strassen算法的基本思想是:
1. 将两个n位数a和b拆分成大约n/2位数的块。例如,1234 = 12, 34;   2345 = 23, 45。
2. 计算所有块之间的乘积,得到4个结果:a1b1, a1b2, a2b1, a2b2。这可以用递归方式计算。
3. 根据分块的位数 Shift 加上进位,得到a1b1*(10^n), a1b2*10^n/2, a2b1*10^n/2, a2b2。
4. 最后将4个结果相加,得到a*b。
5. 例如,计算12345 * 6789:
6. 分块:12, 34,   67, 892. 计算块间乘积:12 * 67 = 804,   12 * 89 = 1068, 34 * 67 = 2298, 34 * 89 = 3026 
7. Shift并加进位:804 * 10000, 1068 * 5000, 2298 * 5000, 30264. 
8. 相加:8040000 + 5340000 + 11490000 + 15130000 = 123456791这种算法通过分块和递归减少每一步的计算量,在计算两个大整数的乘积时有很高的效率,尤其适用于超长整数的相乘。它在一定程度上简化了超长整数运算,是数论和计算机科学中很有价值的一种算法。

优化 误差分析 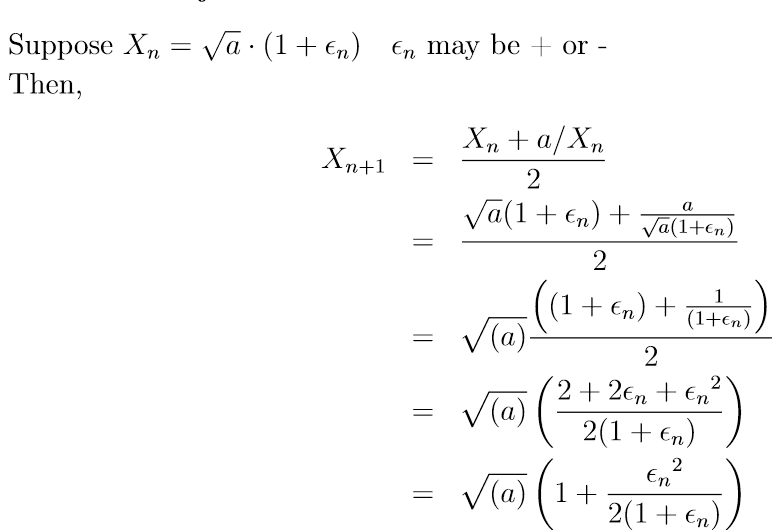\[ ε_{n+1} = \frac{ε_n^2}{2*(1+ε_n)} \]

高精度除法

a/b -> 1/b*a - > mod(R/b) // R是一个容易除的较大值

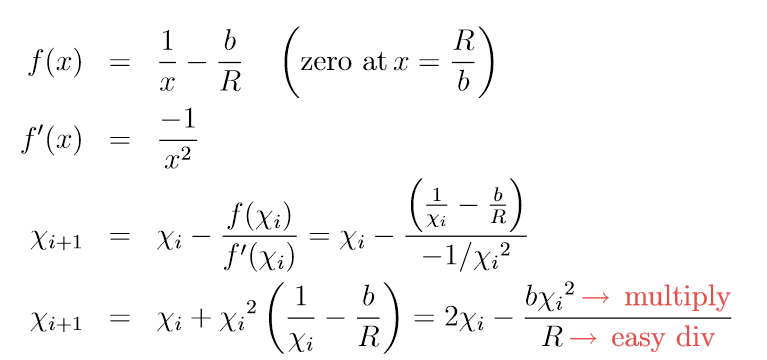
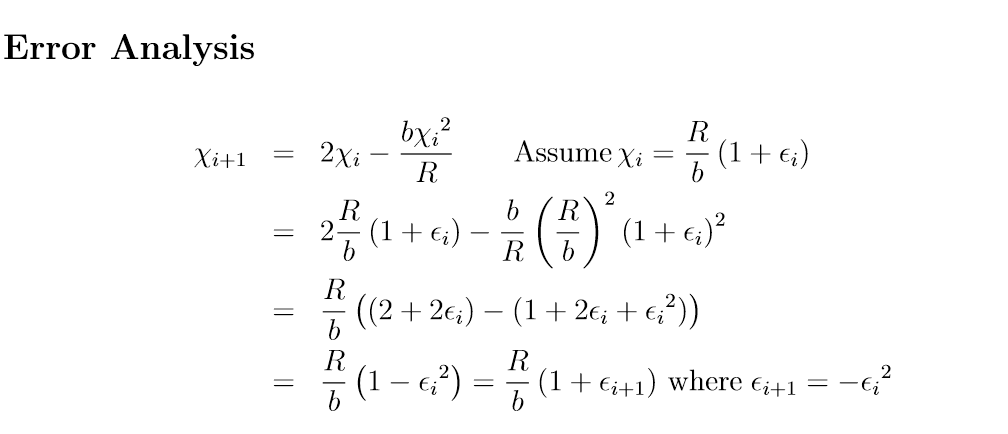除法的复杂度等于乘法 To understand this, assume that the complexity of multiplication is Θ(nα) for n- digit numbers, with α ≥ 1. Division requires multiplication of different-sized numbers at each iteration. Initially the numbers are small, and then they grow to d digits.

We apply a first level of Newton’s method to solve f (x) = x2 − a. Each iteration of this first level1 requires a division. If we set the precision to d digits right from the beginning, then convergence at the first level will require lg d iterations. This means the complexity of computing a square root will be Θ(dα lg d) if the complexity of multiplication is Θ(dα), given that we have shown that the complexity of division is the same as the complexity of multiplication. However, we can do better, if we recognize that the number of digits of precision we need at beginning of the first level of Newton’s method starts out small and then grows. If the complexity of a d-digit division is Θ(dα), then a similar summation to the one above tells us that the complexity of computing square roots is Θ(dα)

图论

概念

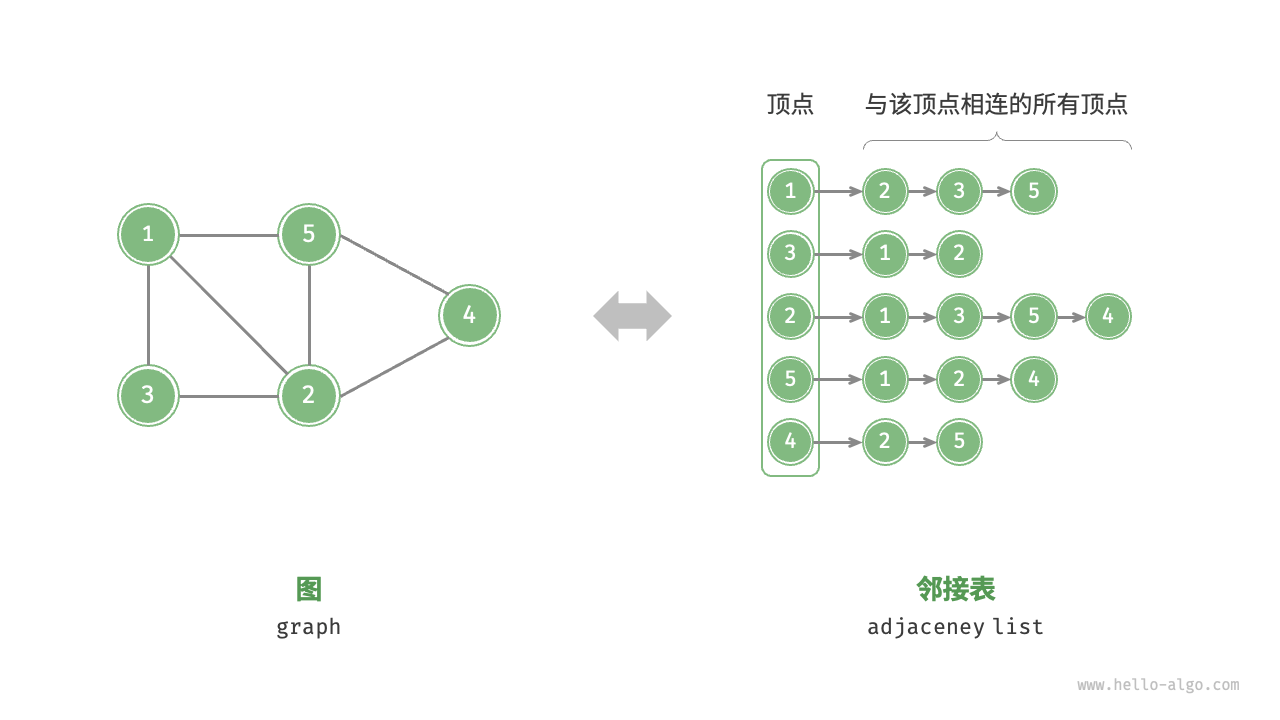
图：for each vertex u ∈ V, Adj[u] stores u’s neighbors, i.e., {v ∈ V | (u, v) ∈ E}. Adj 的大小为 θ(|V |)，而每个 Adj(u) 的大小为 θ(deg(u))

表示分为邻接表和邻接矩阵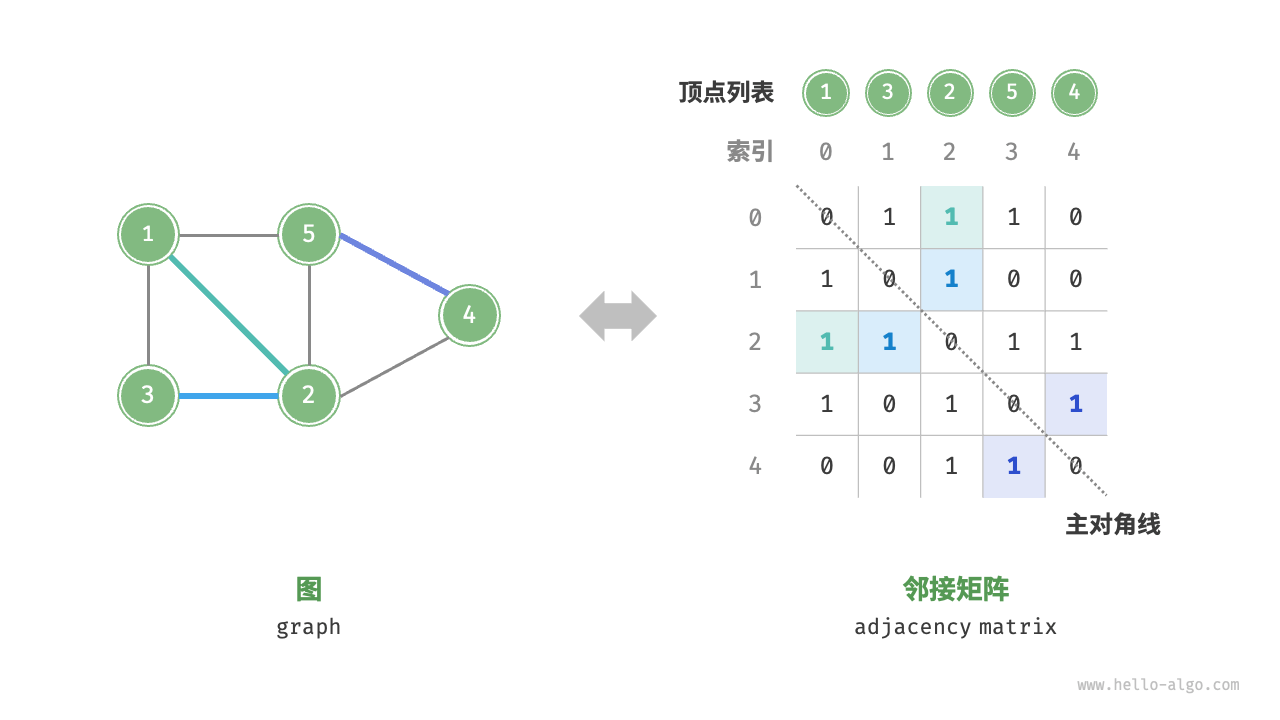

路径

路径是顶点序列p=(v1,v2,...,vk),其中(vi,vi+1)∈E, 1≤i<k
如果路径上没有重复顶点,则为简单路径
路径p的长度为路径上的边数
u到v的距离δ(u,v)为从u到v的最短路径长度

路径问题:

图中的多种路径问题:
  - 单源可达性:s是否可达t
  - 单源最短路径:返回δ(s,t)和s到t的最短路径
  - 单源最短路径:返回从s到所有v的δ(s,v)和最短路径树
如何对每个顶点返回从源s的最短路径?
返回所有路径需Ω(|V|^2)时间
只存储每个v的父节点P(v),s的父节点为空
父节点构成包含从s可达所有最短路径的最短路径树,大小为O(|V|)

BST

应用

网络抓取（Google 如何查找页面）
社交网络（Facebook 好友查找器）
网络广播路由
垃圾收集
模型检查（有限状态机）
检查数学猜想
解决谜题和游戏

如何计算图中所有顶点v的δ(s,v)和P(v)?

使用集合数据结构来存储每个顶点v对应的δ(s,v)距离和P(v)父节点。
如果从起点s到v没有路径,则不存储在P中,δ(s,v)设为无穷大。

基本思路: - 按照与起点s的距离依次增大的顺序探索图的节点。

目标:
- 计算所有与起点s距离为i的顶点的集合Li。结论:
- Li中的任意顶点v必须与L_{i-1}中的某个顶点u相连。
- 不会有任何距离起点距离为j(j<i)的顶点出现在Li中。

循环不变量:
- 在计算到Li之前,δ(s,v)和P(v)对于所有Lj(j<i)中的顶点v都已正确赋值。

BFS (V,Adj,s): See CLRS for queue-based implementation
    level = { s: 0 }
    parent = {s : None }
    i = 1
    frontier = [s] # previous level, i − 1
    while frontier:
        next = [ ] # next level, i
        for u in frontier:
            for v in Adj [u]:
                if v not in level: # not yet seen
                    level[v] = i # = level[u] + 1
                    parent[v] = u
                    next.append(v)
        frontier = next
        i + =1

def graph_bfs(graph: GraphAdjList, start_vet: Vertex) -> list[Vertex]:
    """广度优先遍历 BFS"""
    # 使用邻接表来表示图，以便获取指定顶点的所有邻接顶点
    # 顶点遍历序列
    res = []
    # 哈希表，用于记录已被访问过的顶点
    visited = set[Vertex]([start_vet])
    # 队列用于实现 BFS
    que = deque[Vertex]([start_vet])
    # 以顶点 vet 为起点，循环直至访问完所有顶点
    while len(que) > 0:
        vet = que.popleft()  # 队首顶点出队
        res.append(vet)  # 记录访问顶点
        # 遍历该顶点的所有邻接顶点
        for adj_vet in graph.adj_list[vet]:
            if adj_vet in visited:
                continue  # 跳过已被访问过的顶点
            que.append(adj_vet)  # 只入队未访问的顶点
            visited.add(adj_vet)  # 标记该顶点已被访问
    # 返回顶点遍历序列
    return res

基本情况(i=1):

L0={s},δ(s,s)=0,P(s)=None归纳步骤: (L表示level)
计算Li时:
  - 对Li-1中的每个顶点u:
    - 对于任一不在Lj(j<i)中的相邻顶点v:
      - 将v加入Li,设置δ(s,v)=i,P(v)=u重复计算:
按i递增顺序重复计算Li,直到Li为空集
对任一不可达顶点v,设置δ(s,v)=∞
因此通过归纳证明,广度优先搜索可以正确计算所有δ(s,v)和P(v)。

时间复杂度分析:

用支持快速遍历和插入的数据结构存储Li
通过检查P来判断一个顶点是否在Lj(j<i)中
用支持O(1)操作的字典结构存储δ和P
每个顶点u最多加入一个Li,并对每个邻点v做O(1)操作
以上这些部分是O(|E|)
最后处理不可达顶点需O(|V|)
所以总时间复杂度是O(|V|+|E|)

\[ level[v] = \begin{cases} level & \text{if } v \text{ assigned level} \\\\ \infty & \text{else (no path)} \end{cases} \]

DST

基本思想:

递归访问出边邻接顶点,但不重复访问已访问过的顶点。
尽可能深入探索路径,直到无法继续,然后回溯找到未探索的路径。执行步骤:
初始化P(s)=None,执行visit(s)过程:
- 对每个未在P中出现的邻接顶点v:设P(v)=u并递归调用visit(v)
- 标记访问完顶点u(用于拓扑排序) 不用返回distance,因此时间是O(E)

全BFS和全DFS:

目标是探索整个图,而不仅仅是一个源点可达的部分。
重复在任一未访问顶点s上运行BFS或DFS,直到所有顶点都被访问。
时间复杂度都是O(|V| + |E|)

连通分量:

将无向图的顶点集分割成子集Vi,使每个Vi内部连通,Vi之间无边。连通性算法:
任意单源可达性算法A都可以求解连通分量。
重复运行全A,每次A访问的顶点集就是一个连通分量。

连通性算法:

任意单源可达性算法A都可以求解连通分量。
重复运行全A,每次A访问的顶点集就是一个连通分量。

parent = {s: None}
DFS-visit (V, Adj, s):
    for v in Adj [s]:
        if v not in parent:
            parent [v] = s
            DFS-visit (V, Adj, v)
DFS (V, Adj):
    parent = { }
    for s in V:
        if s not in parent:
            parent [s] = None
            DFS-visit (V, Adj, s)

O(V + E)

总结：

Single-Source Shortest Paths with BFS in O(|V | + |E|) time (return distance per vertex)
Single-Source Reachability with BFS or DFS in O(|E|) time (return only reachable vertices)
Connected components with Full-BFS or Full-DFS in O(|V | + |E|) time
Topological Sort of a DAG with Full-DFS in O(|V | + |E|) time

拓扑排序算法

DFS访问每个顶点v时,记录DFS结束顺序finish[v]
按finish[v]递减顺序输出顶点具体步骤:

通过DFS遍历图
将顶点按finish[v]时间降序插入order
将order反转 正确性证明:
对任意边(u,v)有u在v之前

如果u先访问:
- 在访问u结束前会访问v(直接或间接)
- 因此v结束时间在u之前
如果v先访问:
  - 图无环
  - 无法从v访问u
  - 因此v结束时间在u之前因此DFS结束时间递减顺序即为拓扑排序顺序。

循环检测算法

利用全DFS检测环:

如果无向图无环,全DFS的反序order就是拓扑排序。
对每条边 (u, v)，反序中如果v不在u前，就有环
可以在O(|E|)时间内检测反序是否有环（哈希或者数组的数据结构）

定位环的算法:

在全DFS过程中维护当前顶点的祖先集合
如果DFS遍历到一条从v到其祖先的边,则存在环。

正确性证明:

设图包含环(v0,v1,...,vk,v0),假设v0首先被DFS访问。
对每个vi,在访问vi结束前会访问vi+1并结束。
最后在访问vk结束前会访问v0,此时v0是vk的祖先。

最短路径

路径π的权重w(π)是路径上所有边权重之和
s到t的最短路径是从s到t权重最小的路径
δ(s,t)表示从s到t的最短路径权重
对一般权图,还不知道O(|V|+|E|)的最短路径算法
但对DAG可以在O(|V|+|E|)时间内求解

简单最短路径

简单的最短路径 • 如果图表包含循环和负权重，则可能包含负权重循环 • 如果图形不包含负权环，则最短路径很简单！ • 主张 1：如果 δ(s, v) 是有限的，则存在一条到 v 的最短路径，该路径很简单 • 证明：通过反证法： – 假设没有简单的最短路径；设 π 为顶点最少的最短路径 – π 不简单，所以 π 中存在环 C； C 具有非负权重（或者 δ(s, v) = −∞） – 从 π 中删除 C 形成路径 π0，具有更少的顶点和权重 w(π0) ≤ w(π) • 由于简单路径不能重复顶点，因此有限最短路径最多包含 |V | − 1 条边

有权图基础

最小生成树

If know δ(s, v) for all vertices v ∈ V , can construct shortest-path tree in O(|V | + |E|) time

Initialize empty parent pointer P and set P(s) = NoneFor each vertex u ∈ V where δ(s, u) is finite:  
  For each outgoing neighbor v ∈ Adj+(u):  
    If P(v) is not assigned and δ(s, v) = δ(s, u) + w(u, v):  
      There exists a shortest path through edge (u, v), so set P(v) = uParent pointers may traverse cycles of zero weight. Mark each vertex in such a cycle.For each unmarked vertex u ∈ V (including vertices later unmarked):  
  For each v ∈ Adj+(u) where v is marked and δ(s, v) = δ(s, u) + w(u, v):  
    Unmark vertices in cycle containing v by traversing parent pointers from v  
    Set P(v) = u, breaking the cycle

初始化父节点指针P，设置P(s)为空
对u的每条出边通向的节点v
如果P(v)为空且s->v最短路径是s->u->v,则P(v)=u
父节点可能导致一个权值为0的循环，如果有环则标记出来
对每个没有被标记的u(包括之后会被标记的)
如果有标记的邻居v满足最短路径条件
通过遍历v的父节点清除对它和它的父节点的标记
设置P(v)=u，打破循环

DAG松弛算法:

对每个顶点v维护一个距离估计d(s,v),初始化为无穷大,始终上界真实最短距离δ(s,v)
当边(u,v)违反三角不等式时,通过松弛操作将d(s,v)降低为d(s,u)+w(u,v)
松弛操作保证了d(s,v)始终是到v的某条路径的权重(或无穷大)
算法流程:
  - 初始化d(s,v)=无穷大,d(s,s)=0
   - 按拓扑排序顺序遍历每个顶点u
     - 对每个出边(u,v),如果d(s,v) > d(s,u)+w(u,v),执行松弛操作
可以证明当算法结束时,d(s,v)=δ(s,v),即正确计算出最短距离
时间复杂度为O(V+E),是线性时间算法
主要思想是利用DAG没有环的特点,通过松弛操作逐步收紧距离上界,直到使其等于最短距离
利用拓扑排序的顺序,保证每次松弛时通过的顶点u的d(s,u)已经是最短距离

Generic S.P. Algorithm通用最短路径算法


Initialize:            for v in V:
                            d[v] ← ∞
                            Π[v] ← NIL
                        d[s] ← 0

Main:                  Repeat
                       select edge (u, v)
Relax edge (u, v):         if d[v] > d[u] + w(u, v):
                               d[v] ← d[u] + w(u, v)
                               Π[v] ← u
                        until you can’t relax any more edges or you’re tired or . .

从 u 到 v 的最短路径权重是 δ(u, v)。如果从 u 无法到达 v，则 δ(u, v) 为 Infini，如果从 u 到 v 的某个路径上存在负循环，则未定义。 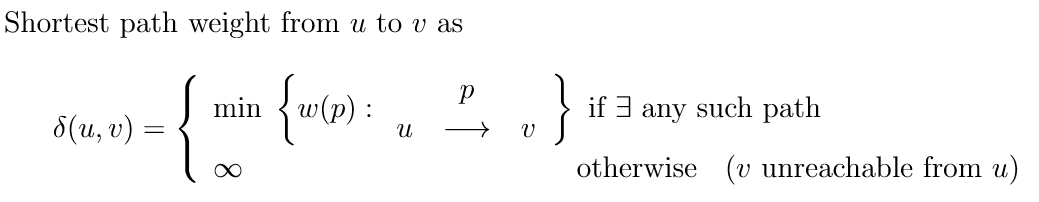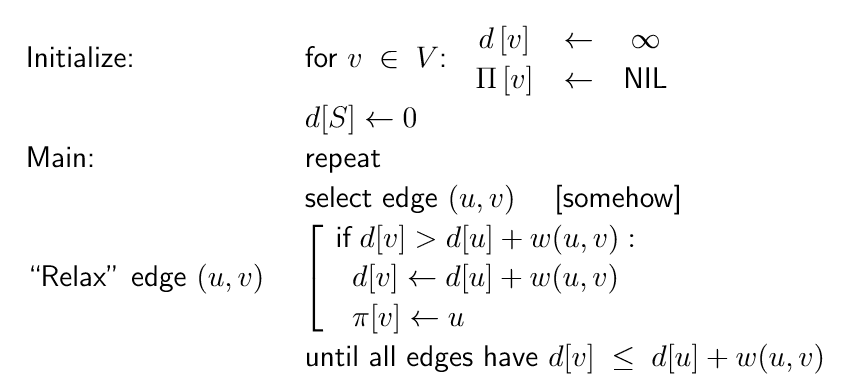PATHological示例:设置n个节点,前3对节点的边权为2^{n/2,第二组节点边权为2}(n/2)-1,以此类推。这样设置权重,从v0到vn-1的距离约为2^{n。算法可能每次只将距离减少1,需重复2}n次,时间复杂度为O(2^n)。因此最短路径算法的性能很大程度上取决于图的结构,存在PATHological情况时算法效率很低。需设计改进的算法,避免指数时间复杂度。

迪杰斯特拉（无负数边的图）

初始化:对每个顶点v,设置d(s,v)=∞,d(s,s)=0。
构建一个优先队列Q,每个顶点v以(v,d(s,v))为项加入Q。
循环直到Q为空:
   - 出队Q中key最小的顶点u
   - 对每个出边(u,v):
      - 如果d(s,v) > d(s,u) + w(u,v):
         - 进行松弛操作         - 降低Q中v的key值到新的d(s,v)
时间复杂度O(E+VlogV),使用二叉堆可以达到O(E+VlogV)

演示 1. 对每个边(u,v),假设权重w(u,v)≥0,维护一个集合S,包含已确定最短路径权重的顶点。 2. 重复地从V-S中选择一个离源点最近的顶点u,将u加入S,松弛u的所有出边,即比较点u连通的其他节点，从点u出发的路径是否比距离表内的短 3. 伪代码:


Dijkstra (G, W, s) //uses priority queue Q
 Initialize (G, s)
 S ← φ
 Q ← V [G] //Insert into Q
 while Q != φ
  do u ← EXTRACT-MIN(Q) //deletes u from Q
  S = S ∪ {u}
  for each vertex v ∈ Adj[u]
   do RELAX (u, v, w) ← this is an implicit DECREASE KEY operation


RELAX(u, v, w)
 if d[v] > d[u] + w(u, v)
  then d[v] ← d[u] + w(u, v)
  Π[v] ← u
放松是安全的
 引理：松弛算法对于所有的情况都保持 d[v] ≥ δ(s, v) 的不变量
 v ∈ V 。
 证明：通过步数归纳。
 考虑 RELAX(u, v, w)。  通过归纳法 d[u] ≥ δ(s, u)。  通过三角形 -
 等式，δ(s, v) ≤ δ(s, u) + δ(u, v)。  这意味着 δ(s, v) ≤ d[u] + w(u, v)，因为
 d[u] ≥ δ(s, u) 且 w(u, v) ≥ δ(u, v)。  因此设置 d[v] = d[u] + w(u, v) 是安全的。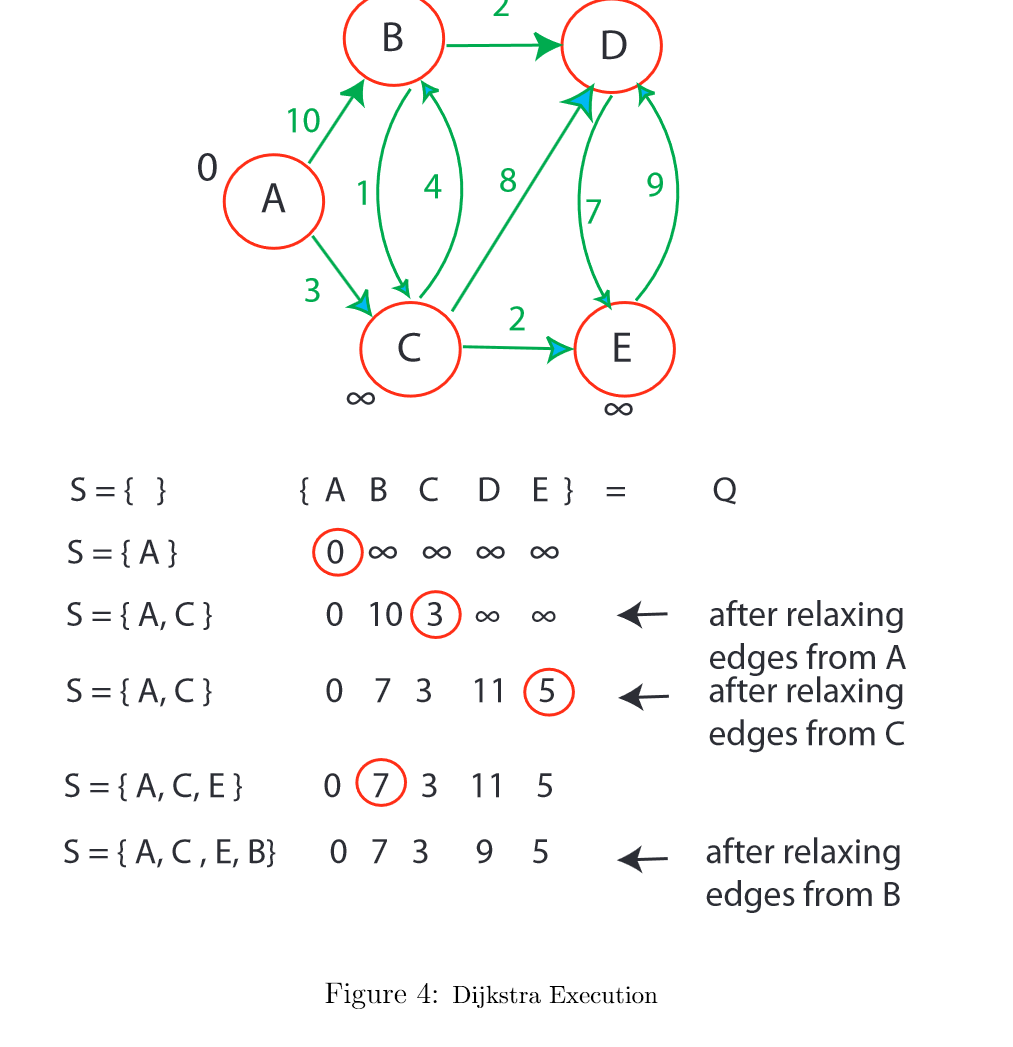

4. 通过重复选择最近顶点,逐步确定最短路径,时间复杂度为O(|E|+|V|log|V|)。

证明

归纳法证明当顶点v从Q中取出时,d(s,v) = δ(s,v)成立: 基础:s第一个取出,d(s,s)=0 = δ(s,s)成立 - 归纳假设:对前k-1个顶点成立 - 考虑第k个顶点v0: - 取v0到s的最短路径π,w(π)=δ(s,v0) - 设(x,y)是π中第一个y不在前k-1个顶点的边 - 当x取出时,d(s,x)=δ(s,x)(归纳假设) - 所以取出x时松弛(x,y),d(s,y) ≤ δ(s,x) + w(x,y) = δ(s,y) - 由于松弛操作的安全性,d(s,v0) ≤ δ(s,v0) - 又因为v0是Q中key最小的,d(s,v0) ≥ δ(s,v0) - 所以d(s,v0) = δ(s,v0)

时间复杂度

操作 | 时间复杂度 | 在Dijkstra中的出现次数|

|-|-|-|
|Q.build(X) (n = |X|)| Bn | 1 |
|Q.delete min()| Mn | |V| |
|Q.decrease key(id, k)| Dn | |E| | 总计O(B|V | + |V | · M|V | + |E| · D|V |) 对一个对顶点所有节点可达的图（修建过）：对不同稀疏密度的图,使用不同的数据结构实现Dijkstra算法可以得到不同的时间复杂度: - 如果图是密集的,即 |E| = Θ(|V|^{2),使用数组实现优先队列Q,时间复杂度为O(|V|}2) - 如果图是稀疏的,即 |E| = Θ(|V|),使用二叉堆实现Q,时间复杂度为 O(|V|log|V|) - Fibonacci堆在理论上对任意图都很好,但是实践中不常用 - 在理论分析中,通常假设Dijkstra算法的时间复杂度为O(|E| + |V|log|V|) 总结


Dijkstra Complexity
 Θ(v) inserts into priority queue
 Θ(v) EXTRACT MIN operations
 Θ(E) DECREASE KEY operations
Array impl:
 Θ(v) time for extra min
 Θ(1) for decrease key
 Total: Θ(V.V + E.1) = Θ(V 2 + E) = Θ(V 2)
Binary min-heap:
 Θ(lg V ) for extract min
 Θ(lg V ) for decrease key
 Total: Θ(V lg V + E lg V )
Fibonacci heap (not covered in 6.006):
 Θ(lg V ) for extract min
 Θ(1) for decrease key
 amortized cost
 Total: Θ(V lg V + E)

优化——双向搜索

如果只需要s到t的最短路径，则只需要进行到t出队时结束算法 1. 双向搜索可以加速搜索,但不改变最坏时间复杂度,实际上可以减少访问的节点数。 2. 双向搜索同时进行: - 从s节点进行正向搜索 - 从t节点进行反向搜索(沿边反向移动) 3. 正向搜索距离标记为df(u),反向为db(u) 4. 当一个节点w同时被两边搜索删除出队列时,搜索终止。 5. 终止后,找到df(x)+db(x)最小的节点x,x不一定是终止节点w。 6. 使用正向predecessor树Πf找到s到x的最短路径,使用反向树Πb找到t到x的最短路径。 7. 节点x一定已经被某一边搜索删除出队列。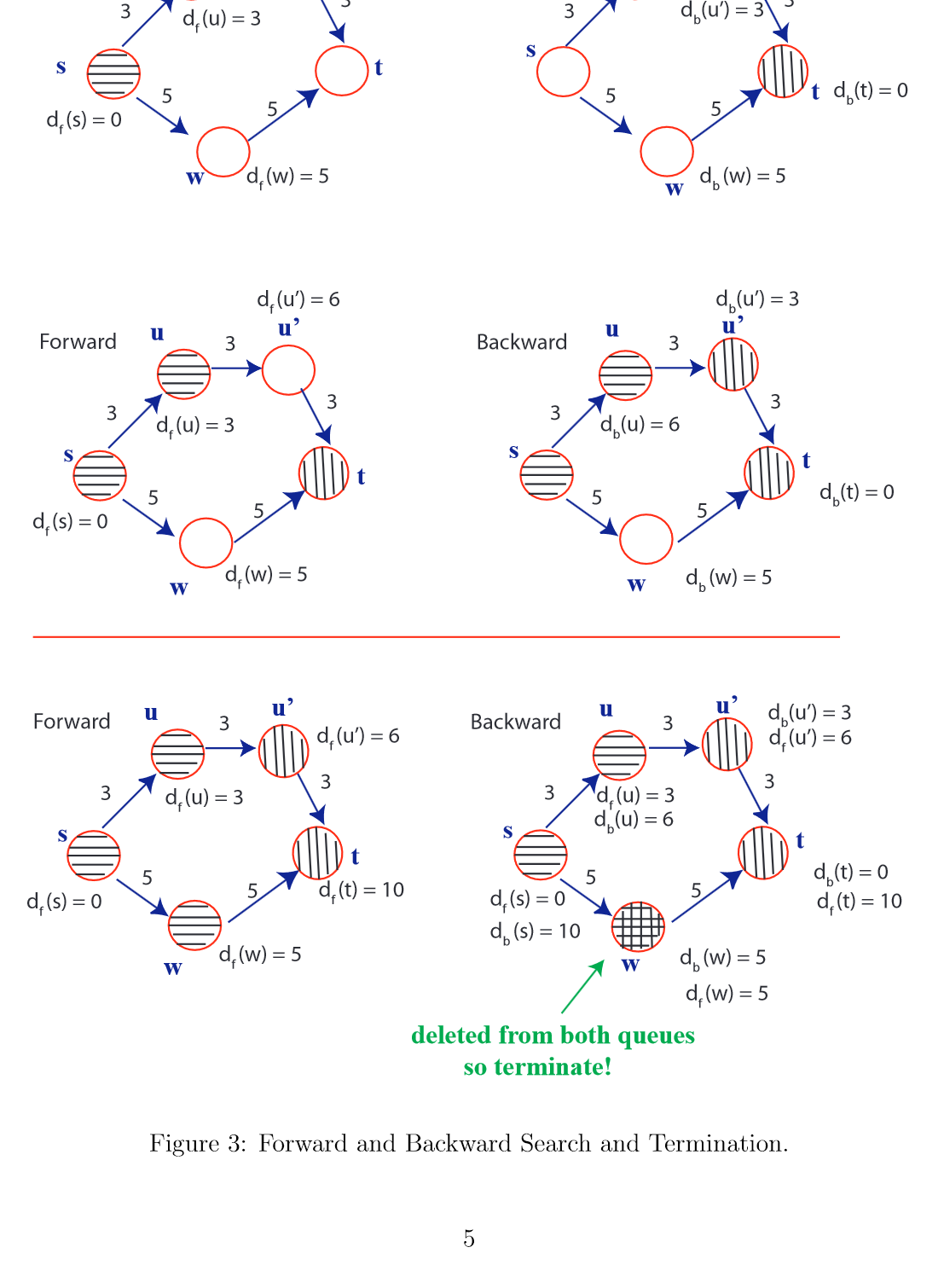

A*算法

A*通过势函数修改边权重指引搜索方向:w'(u,v) = w(u,v) - λ(u) + λ(v)
选择势函数使修改后的权重保持最短路径不变,且权重非负,以适用于Dijkstra算法。
设定目标势值为0,源点势值足够大,可以引导搜索方向。
使用landmark技巧:预计算顶点到一些landmark节点的最短距离δ(u,l)。定义势函数λ(u)=δ(u,l)-δ(t,l),可以证明是可行的。
对每个landmark l计算势函数λ,取最大值作为最终势函数,仍可行。
A*相比普通搜索可以显著减少搜索范围,提高效率。但最坏情况时间复杂度未改变。

Modify edge weights with potential function over vertices \[ \overline{w}(u, v) = w(u, v) - λ(u) + λ(v) \]

So shortest paths are maintained in modified graph with w(overline) weights \[ \overline{w}(p) = w(p) - λ_t(u) + λ_t(t) \] Small set of landmarks LCV . For all u ∈ V, l ∈ L, pre-compute δ(u, l). Potential \[ λ_t^{(l)}(u) = δ(u, l) − δ(t, l) \]

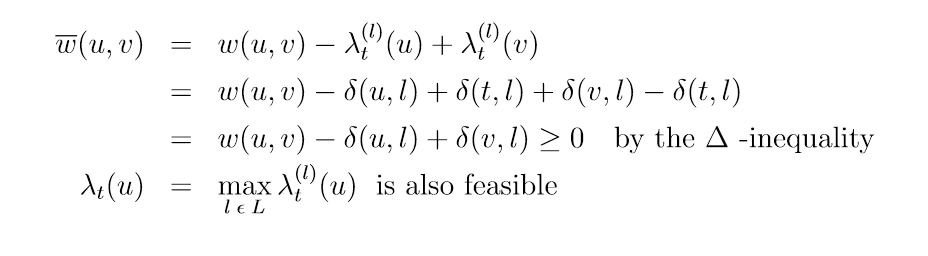
贝尔曼福特

负循环检测

定义k边距离δk(s,v):从s到v的路径中最多包含k条边的最小路径权重。
计算出δ|V|-1(s,v)和δ|V|(s,v),如果δ|V|(s,v)<δ|V|-1(s,v),则v是一个负环见证人(witness)。
任意有向图中，对每个v∈V，计算δ(s,v)和δ|V|-1(s,v):
- 如果δ(s,v)<δ|V|-1(s,v),则δ|V |(s, v) =- ∞，把v视为负循环见证人 - 如果δ(s,v)!=−∞,则δ(s,v)=δ|V|-1(s,v)(简单最短路径原理) - 如果δ(s,v)=−∞,v可以从某个见证人出发而到达
证明思路:

假设某个负环C可达且不包含见证人,则对C中任一顶点v有:
δ|V|(s,v) ≤ δ|V|-1(s,v的前驱)+w(v的前驱,v) < δ|V|-1(s,v)
矛盾,所以C中必须存在见证人。

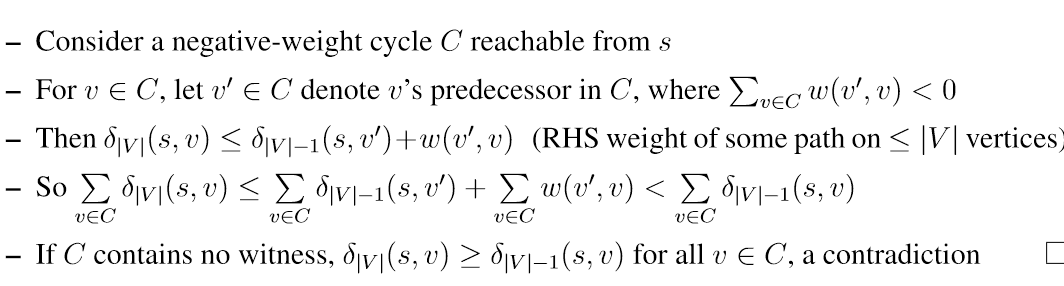
定义

正确性： s到vk(k表示层数)的最短路径是每层可能的路径的最短者，贝尔曼福特算法穷举每一种可能，所以最后能得出最短的|V|-1层路径，从|V|-1到|V|则取决于图有没有负循环，如果有负循环，则s到见证人可达的结点路径为负无穷长运行时间 1. 构建多层图G'需O(|V|(|V|+|E|)) 2. 在G'上运行DAG最短路径算法需O(|V|(|V|+|E|))，即G'大小的线性时间 3. 处理每个负环见证人需O(1),找到一个见证人的所有可达结点是O(|E|)见证人最多V个，找到所有见证人的可达性需O(|V||E|) 4. 如果把G修整成s开始的s可达子图，时间复杂度为O(|V||E|)

扩展思考:

• |V | + 1 levels: vertex vk in level k represents reaching vertex v from s using ≤ k edges • If edges only increase in level, resulting graph is a DAG • Construct new DAG G0 = (V 0, E0) from G = (V, E): – G' has |V |(|V | + 1) vertices v_k for all v ∈ V and k ∈ {0, . . . , |V |} – G' has |V |(|V | + |E|) edges: ∗ |V | edges (vk−1, vk) for k ∈ {1, . . . , |V |} of weight zero for each v ∈ V ∗ |V | edges (uk−1, vk) for k ∈ {1, . . . , |V |} of weight w(u, v) for each (u, v) ∈


Bellman-Ford(G,W,s)
 Initialize ()
 for i = 1 to |V | − 1
  for each edge (u, v) ∈ E:
   Relax(u, v)
 for each edge (u, v) ∈ E
  do if d[v] > d[u] + w(u, v)
   then report a negative-weight cycle exists
//At the end, d[v] = δ(s, v), if no negative-weight cycles

1. 初始化,进行|V|-1轮松弛操作,每轮对每个边(u,v)做relax操作，非负的图最多需要|V|-I次操作就可以松弛到任意点出发的任意路径都是最短路径 2. 如果第|V|轮还可以relax任意边,说明存在负权环。 3. 如果图中无负权环,Bellman-Ford执行结束后d[v]=δ(s,v)。 4. 推论:如果d[v]在|V|-1轮未收敛,说明存在从s可达的负权环。 5. Bellman-Ford时间复杂度为O(|V||E|),适合稠密图。

最长简单路径和最短简单路径

在具有非负边权重的图中找到最长的简单路径是一个 NP- hard问题，不存在已知的多项式时间算法。假设一个只需否定每个边权重并运行 Bellman-Ford 来计算最短路径。贝尔曼-福特不一定会计算原始路径中的最长路径图，因为可能存在可从源到达的负权重循环，并且算法将中止。类似地，如果我们有一个具有负循环的图，并且我们希望找到最长的从源 s 到顶点 v 的简单路径，我们不能使用 Bellman-Ford。最短的简单路径问题也是NP- hard问题

Johnson’s Algorithm

All-Pairs Shortest Paths (APSP)

输入:有向带权图G=(V,E),权值函数w:E→Z
输出:对所有u,v∈V,求出δ(u,v),如果有负权回路则报错
应用:理解整个网络,如交通、电路布线、供应链等
直接运行|V|次单源算法时间复杂度:     - DAG松弛: |V|·O(|V|+|E|),无环
  - BFS: |V|·O(|V|+|E|),非负权值
  - Dijkstra: |V|·O(|V|log|V|+|E|),非负权值
  - Bellman-Ford: |V|·O(|V||E|),一般图

思路：重构权值函数,使G变为G',其中G'没有负权边,且G的最短路径在G'上也是最短路径。如果成功,就可以在G'上运行Dijkstra 实现：对每个顶点v:
- 从v出发的边权加上h
- 进入v的边权减去h
- 这样可以保证最短路径不变
- 证明:
  - 任意从v开始的路径权值改变了h
  - 任意到v结束的路径权值改变了-h
  - 通过v的路径权值局部不变

算法

构造含新顶点x的图Gx,x到每个顶点v有权值为0的边
对Gx运行Bellman-Ford算法计算δx(x,v)
如果δx(x,v)为无穷大,说明G中有负权回路,报错退出
否则,用δx重新调整每个边的权值构造G'
对G'运行Dijkstra算法|V|次计算每个顶点的最短路径
从G'的最短路径恢复G的最短路径

时间复杂度

构造Gx需O(|V|+|E|)
Bellman-Ford需O(|V||E|)
构造G'需O(|V|+|E|)
|V|次Dijkstra需O(|V|(|V|log|V| + |E|))
用G'恢复G的距离需O(|V|^2)
总计O({|V|^2}log|V| + |V||E|)

概率

雇佣问题


best = 0
hired = null
for i = 1 to n
if candidates[i] > best
 best = candidates[i]
 hired = i

指示器随机变量

指示器随机变量可以用于对随机输入的算法分析 \[I(A) = \begin{cases} 1 & \text{event A occurs} \\ 0 & \text{otherwise} \end{cases}\] 把期望转化成指示器期望的相加

随机算法

在此基础上可以在算法中进行随机数处理，排除输入的影响比如在雇佣问题中，对输入的候选者数组进行随机排序随机排序：


n = A.length
let P[1-n] be a new array
for i=1 to n
 P[i] = RANDOM(1,n^3)
sort A,use P

递归和动态规划


# recursive solution (top down)
def fib(n):
 memo = {}
 def F(i):
  if i < 2: return i # base cases
  if i not in memo: # check memo
   memo[i] = F(i - 1) + F(i - 2) # relation
  return memo[i]
 return F(n) # original
# iterative solution (bottom up)
def fib(n):
 F = {}
 F[0], F[1] = 0, 1 # base cases
 for i in range(2, n + 1): # topological order
  F[i] = F[i - 1] + F[i - 2] # relation
 return F[n] # original

# recursive solution (top down)
def bowl(v):
 memo = {}
 def B(i):
  if i >= len(v): return 0 # base cases
  if i not in memo: # check memo
  memo[i] = max(B(i+1), # relation: skip pin i
   v[i] + B(i+1), # OR bowl pin i separately
   v[i] * v[i+1] + B(i+2)) # OR bowl pins i and i+1 together
   return memo[i]
  return B(0) # original
# iterative solution (bottom up)
def bowl(v):
 B = {}
 B[len(v)] = 0 # base cases
 B[len(v)+1] = 0
 for i in reversed(range(len(v))): # topological order
  B[i] = max(B[i+1], # relation: skip pin i
   v[i] + B(i+1), # OR bowl pin i separately
   v[i] * v[i+1] + B(i+2)) # OR bowl pins i and i+1 together
 return B[0] # original

如何关联子问题解决方案 • 我们遵循的一般方法来定义子问题解决方案的关系： - 确定一个有关子问题解决方案的问题，如果知道答案，则该问题将减少到“更小的”子问题 - 在打保龄球的情况下，问题是“我们如何打第一对球瓶？” - 然后通过尝试所有可能的答案并采取最好的答案来本地暴力解决问题 - 在保龄球的情况下，我们取最大值，因为问题要求最大化 - 或者，我们可以考虑正确猜测问题的答案，然后直接递归；但随后我们实际上检查所有可能的猜测，并返回“最佳” • 效率的关键是问题有少量（多项式）可能的可能性。答案，所以暴力破解并不太昂贵 • 通常（但并非总是）计算关系的非递归工作等于数字我们正在尝试的答案

动态规划

LCS

• x(i, j) = A[i :] 和 B[j :]的最大公共子序列 • For 0 <= i <= |A| and 0 <=0 j <= |B| 最长公共子序列问题(LCS): 1. 定义了子问题x(i,j),表示 A[i:]和B[j:]的最长公共子序列长度。 2. 列出了递归关系 - 如果A[i]==B[j],那么x(i,j)等于x(i+1,j+1)+1,否则等于x(i+1,j)和x(i,j+1)的最大值。 3. 指出了拓扑顺序,子问题依赖更大的i或j。 4. 给出了 base cases —— 当一个字符串为空时,LCS长度为0。x(i, |B|) = x(|A|, j) = 0 5. 原问题可以通过x(0,0)求解,同时需要parent pointers构建最长子序列。 6. 时间复杂度分析也正确,子问题数为O(|A|*|B|),每件工作为O(1),所以总时间为O(|A|*|B|)。 \[ x(i,j) = \begin{cases} x(i+1,j+1)+1, & \text{if }A[i]=B[j] \\ max(x(i + 1, j), x(i, j + 1)) , & otherwise \end{cases} \]

def lcs(A, B):
 a, b = len(A), len(B)
 x = [[0] * (b + 1) for _ in range(a + 1)]#x 的最终形状是一个 (a + 1) x (b + 1) 的二维列表,每个元素初始化为 0
 for i in reversed(range(a)):
  for j in reversed(range(b)):
   if A[i] == B[j]:
    x[i][j] = x[i + 1][j + 1] + 1
   else:
    x[i][j] = max(x[i + 1][j], x[i][j + 1])
 return x[0][0]
#如果A[i] == B[j],那么最长公共子序列可以在A[i+1:]和B[j+1:]的基础上再加上A[i]这个字符,所以x[i][j] = x[i+1][j+1] + 1。
#如果A[i] != B[j],那么A[i]和B[j]不可能同时在最长公共子序列中,需要舍弃一个字符。所以x[i][j]取x[i+1][j]和x[i][j+1]中的最大值。
#依次遍历,直到i或j变为-1,即遍历完两个字符串。

LIS

Longest Increasing Subsequence (LIS)

def lis(A):
 a = len(A)
 x = [1] * a
 for i in reversed(range(a)):
  for j in range(i, a):
   if A[j] > A[i]:
    x[i] = max(x[i], 1 + x[j])
 return max(x)

x(i)是A[i:]的最长递增子数组 O(|A|^2) running time - 外层循环i是在寻找以每个元素结尾的LIS长度。 - 内层循环j是在寻找可以接在A[i]后面的最大LIS长度。 - x数组缓存了每个位置的LIS长度,避免重复计算。 - 通过从后向前遍历,可以保证每个x[i]都是最新的最大LIS长度。

Alternating Coin Game

两名玩家（“我”和“你”）轮流
轮流取出剩余硬币中的第一个或最后一个硬币
我的目标是最大化我所拿走的硬币的总价值，这是我首先要做的 x(i, j) =我可以从 vi, . . . , vj中拿走的最大硬币总价值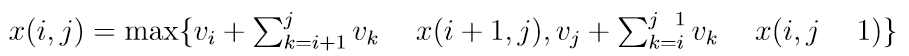子问题: O(n^2) • 每个子问题相加: O(n) to compute sums • O(n^3) running time

优化

扩展定义子问题x(i,j,p),添加了一个表示下一步该谁走的状态p。
列出了四个递归关系式,区分我方走与对方走的不同情况。
拓扑顺序及base case与第一种解法相同。
计算原问题时,状态为我方走。

x(i, j, p) = maximum total value I can take when player p ∈ {me, you} starts from coins of values vi, . . . , vj

Player p must choose either coin i or coin j • If p = me, then I get the value; otherwise, I get nothing • Then it’s the other player’s turn • x(i, j, me) = max{vi + x(i + 1, j, you), vj + x(i, j + 1, you)} • x(i, j, you) = min{x(i + 1, j, me), x(i, j + 1, me)} 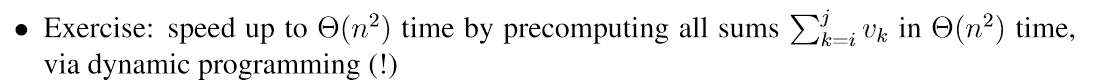时间 • subproblems: ⇥(n2) • work per subproblem: ⇥(1) • ⇥(n2) running time 扩展子问题可以提供递归所需信息,但代价是子问题数目增加,计算复杂度上升。需要权衡取舍。

Rod Cutting

切一根棍子，切割长度产生的收益如表

index	0	1	2	3	4	5	6	7
value	0	1	10	13	18	20	31	32

x(l): maximum value obtainable by cutting rod of length x(l) = max{v(p) + x(l-p) | p 2 {1, . . . ,l }} time: - subproblems: L + 1 - work per subproblem: O(l) = O(L) - O(L^2) running time

# recursive
x = {}
def cut_rod(l, v):
 if l < 1: return 0 # base case
 if l not in x: # check memo
  for piece in range(1, l + 1): # try piece
   x_ = v[piece] + cut_rod(l - piece, v) # recurrence
   if (l not in x) or (x[l] < x_): # update memo
    x[l] = x_
 return x[l]

# iterative
def cut_rod(L, v):
 x = [0] * (L + 1) # base case
 for l in range(L + 1): # topological order
  for piece in range(1, l + 1): # try piece
   x_ = v[piece] + x[l - piece] # recurrence
   if x[l] < x_: # update memo
    x[l] = x_
 return x[L]

# iterative with parent pointers
def cut_rod_pieces(L, v):
 x = [0] * (L + 1) # base case
 parent = [None] * (L + 1) # parent pointers
 for l in range(1, L + 1): # topological order
  for piece in range(1, l + 1): # try piece
   x_ = v[piece] + x[l - piece] # recurrence
   if x[l] < x_: # update memo
    x[l] = x_
    parent[l] = l - piece # update parent
 l, pieces = L, []
 while parent[l] is not None: # walk back through parents
  piece = l - parent[l]
  pieces.append(piece)
  l = parent[l]
 return piece

Subset Sum

相关博客 A = {a0, a1, . . . , an} 是否存在A的子集A'，A'的元素总和为T x(i, j): True if can make sum j using items 1 to i, False otherwis \[ x(i,j) = \begin{cases} x(i - 1, j - A[i]), & \text{if j >= A[i] } \\ x(i - 1, j), & always \end{cases} \] - x(i, 0) = True for i ∈ {0, . . . , n} (trivial to make zero sum!) - x(0, j) = False for j ∈ {1, . . . , T} (impossible to make positive sum from empty set - for i ∈ {0, . . . , n}, j ∈ {0, . . . , T}

import numpy as np

def dp_subset(arr,S):
    
    subset = np.zeros((len(arr),S+1),dtype=bool) #构造二维数组
    subset[:,0] = True # 第一列 设为True
    subset[0,: ] = False #第一列 设为 False
    subset[0,arr[0]] = True
    
    for i in range(1,len(arr)):
        for s in range(1, S+1):
            if arr[i] > s:
                subset[i , s] = subset[i-1 , s]
            else:
                A = subset[i-1 , s ]
                B = subset[i-1 , s - arr[i]]
                subset[i,s] = A or B
                
                
    row ,cell = subset.shape
    return subset[row-1,cell-1]
            
arr  = [1,2, 4,5,6]            
dp_subset(arr,7) 
out:True

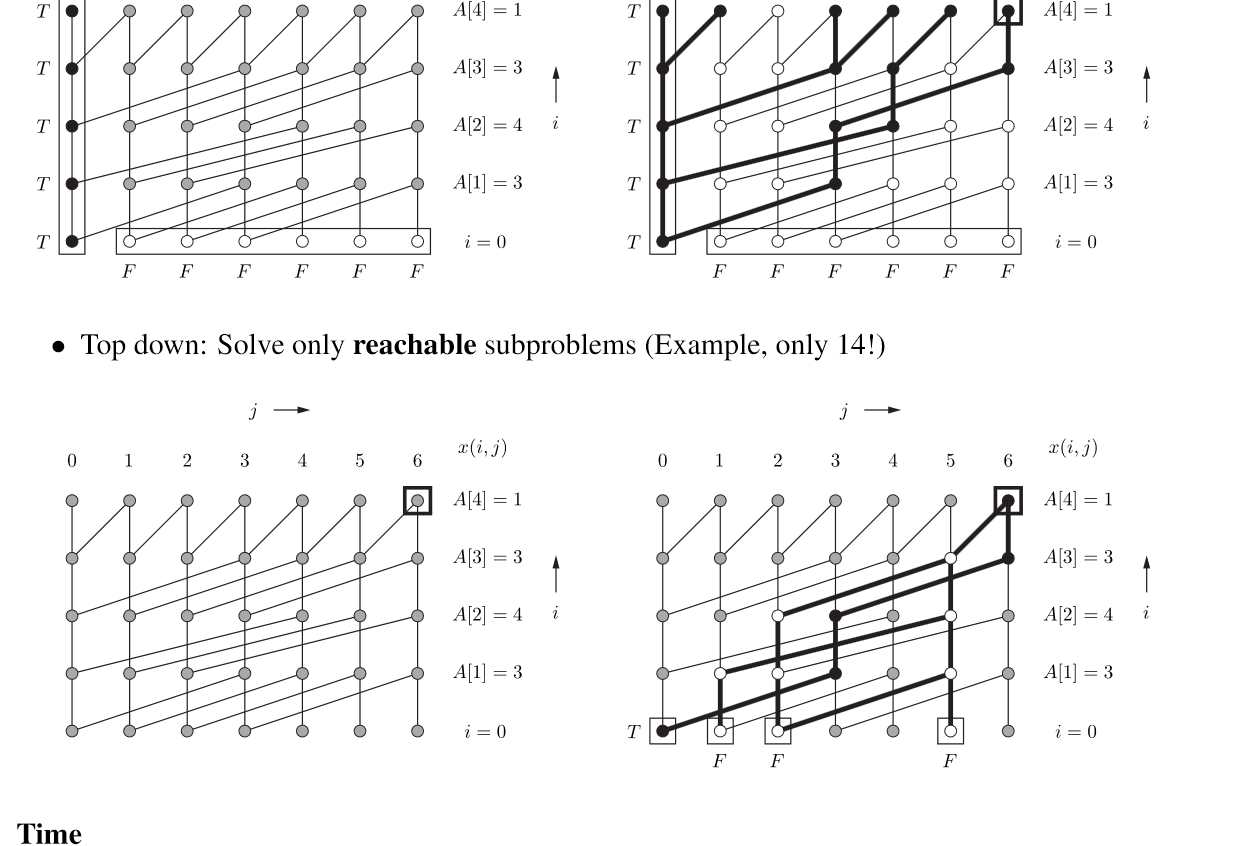
subproblems: O(nT ), O(1) work per subproblem, O(nT ) time

其他

多项式时间的判定

只有在算法时间复杂度仅与问题规模有多项式关系时，才可称为多项式时间复杂度算法。存在如基数排序之类时间复杂度依赖于输入数据的算法，称为伪多项式时间复杂度，此时算法的时间复杂度是输入数据大小的多项式时间表达，但却是输入数据长度（输入规模）的指数时间表达

例子：
冒泡排序：给定 n 个64位的数字，进行 n-1 次扫描交换，将数字从小到大排序。
素数测试：给定数字 n，通过从 2 到根号 n 的整数遍历，判断 n 是否为素数。
字面上看，两者复杂度都是 O(n^k) ( k 为整数) 。但区别在于，前者的 n 是数字个数的多少，后者的 n 是数字的大小。
因此，前者输入总规模 s1 增长与数字大小无关，s1 = 64n；后者增长规模与数字大小紧密相关，输入总规模为 s2 = logn 。
所以可知冒泡排序中复杂度 O(n^2) = O(s1^2/64^2) 为多项式算法，后者素数测试O(n) = O(2^(s2)) 为伪多项式算法

复杂度

决策问题:将输入归类为YES或NO的问题。
算法/程序:能够在一定时间内解决问题的常量长度代码。
如果问题有算法可以在有限时间内解决,则该问题是可判定的。
程序是有限的,问题是无限的,因此大多数决策问题是不可判定的。
即使可判定,也以不同的时间复杂度分类:

R类:有限时间可判定
EXP类:指数时间可判定
P类:多项式时间可判定(我们关注的)

这些类满足 P⊆EXP⊆R 的包含关系。 NP与P问题参考61b笔记

mit的后续课程