基于加州房地产数据集的数据分析项目

发表于 更新于 分类于 ， 阅读次数： 本文字数： 3.9k 阅读时长 ≈ 14 分钟

实践报告

背景介绍

本次作业使用一个房价数据集，房价数据集完全由数字信息构成，规模属于中小级别(2w条左右)，有一定的数据处理需求，但由于最主要的参数房价和其他相关列主要是简单的类线性关系，易于作为学习数据科学的入门材料。
此外，通过房屋参数来预测房价在现实中也有一定的实践意义，例如一些房屋出售软件可以建立相关模型来给出估价等。

问题描述

主要目标是预测房价，为此目标，需要清洗不合理的数据，寻找线性相关的列，最后利用一些回归模型来进行训练，并验证结果 最后的输入是数据集内和房价线性相关程度较高的列，输出则是对房价的预测结果。

数据描述

这些数据涉及在加州某个地区的街区以及基于 1990 年人口普查数据的一些汇总统计数据：

  1. 房屋中位价值：一个街区内家庭的房屋中位价值（以美元计算）
  2. 收入中位数：一栋房屋内的家庭收入中位数（以万美元衡量）
  3. 中位年龄：街区内房屋的中位年龄； 数字较小的是较新的建筑
  4. 房间总数：一个街区内的房间总数
  5. 卧室总数：一个街区内的卧室总数
  6. 人口：居住在一个街区内的总人数
  7. 家庭：一个街区的家庭总数
  8. 纬度：衡量房屋向北有多远的指标； 值越高越北 [°]
  9. 经度：衡量房屋向西有多远的量度； 数值越高，越西 [°]
  10. 距离海岸：到最近海岸点的距离[m]
  11. 到洛杉矶的距离：到洛杉矶市中心的距离[m]
  12. 到圣地亚哥的距离：到圣地亚哥中心的距离[m]
  13. 到圣何塞的距离: 到圣何塞中心的距离 [m]
  14. 到旧金山的距离：到旧金山市中心的距离[m]
  1. Median House Value: Median house value for households within a block (measured in US Dollars)
  2. Median Income: Median income for households within a block of houses (measured in tens of thousands of US Dollars)
  3. Median Age: Median age of a house within a block; a lower number is a newer building [years]
  4. Total Rooms: Total number of rooms within a block
  5. Total Bedrooms: Total number of bedrooms within a block
  6. Population: Total number of people residing within a block
  7. Households: Total number of households, a group of people residing within a home unit, for a block
  8. Latitude: A measure of how far north a house is; a higher value is farther north [°]
  9. Longitude: A measure of how far west a house is; a higher value is farther west [°]
  10. Distance to coast: Distance to the nearest coast point [m]
  11. Distance to Los Angeles: Distance to the centre of Los Angeles [m]
  12. Distance to San Diego: Distance to the centre of San Diego [m]
  13. Distance to San Jose: Distance to the centre of San Jose [m]
  14. Distance to San Francisco: Distance to the centre of San Francisco [m]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
#引入python库
import numpy as np

import pandas as pd

%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
warnings.filterwarnings('ignore')
#固定随机结果
np.random.seed(44)
#读取数据集
training_data = pd.read_csv('California_Houses.csv')
1
training_data.columns.values
array(['Median_House_Value', 'Median_Income', 'Median_Age', 'Tot_Rooms',
       'Tot_Bedrooms', 'Population', 'Households', 'Latitude',
       'Longitude', 'Distance_to_coast', 'Distance_to_LA',
       'Distance_to_SanDiego', 'Distance_to_SanJose',
       'Distance_to_SanFrancisco'], dtype=object)
1
training_data.describe()
Median_House_Value Median_Income Median_Age Tot_Rooms Tot_Bedrooms Population Households Latitude Longitude Distance_to_coast Distance_to_LA Distance_to_SanDiego Distance_to_SanJose Distance_to_SanFrancisco
count 20640.000000 20640.000000 20640.000000 20640.000000 20640.000000 20640.000000 20640.000000 20640.000000 20640.000000 20640.000000 2.064000e+04 2.064000e+04 20640.000000 20640.000000
mean 206855.816909 3.870671 28.639486 2635.763081 537.898014 1425.476744 499.539680 35.631861 -119.569704 40509.264883 2.694220e+05 3.981649e+05 349187.551219 386688.422291
std 115395.615874 1.899822 12.585558 2181.615252 421.247906 1132.462122 382.329753 2.135952 2.003532 49140.039160 2.477324e+05 2.894006e+05 217149.875026 250122.192316
min 14999.000000 0.499900 1.000000 2.000000 1.000000 3.000000 1.000000 32.540000 -124.350000 120.676447 4.205891e+02 4.849180e+02 569.448118 456.141313
25% 119600.000000 2.563400 18.000000 1447.750000 295.000000 787.000000 280.000000 33.930000 -121.800000 9079.756762 3.211125e+04 1.594264e+05 113119.928682 117395.477505
50% 179700.000000 3.534800 29.000000 2127.000000 435.000000 1166.000000 409.000000 34.260000 -118.490000 20522.019101 1.736675e+05 2.147398e+05 459758.877000 526546.661701
75% 264725.000000 4.743250 37.000000 3148.000000 647.000000 1725.000000 605.000000 37.710000 -118.010000 49830.414479 5.271562e+05 7.057954e+05 516946.490963 584552.007907
max 500001.000000 15.000100 52.000000 39320.000000 6445.000000 35682.000000 6082.000000 41.950000 -114.310000 333804.686371 1.018260e+06 1.196919e+06 836762.678210 903627.663298

数据处理

导入python库

封装函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#数据清洗函数
def remove_outliers(data, variable, lower=-np.inf, upper=np.inf):
    df = data.copy()
    df = df[df[variable] > lower]
    df = df[df[variable] < upper]
    return df
    
#划分训练集和验证集
def train_val_split(data, train_pct=0.8):
    data_len = data.shape[0]
    shuffled_indices = np.random.permutation(data_len)
    
    split_index = int(0.8 * data_len)
    train_indices = shuffled_indices[:split_index]
    val_indices = shuffled_indices[split_index:]
    
    train = data.iloc[train_indices]
    validation = data.iloc[val_indices]

    return train, validation
    
#绘制分布图和箱型图
def plot_distribution(data, label):
    fig, axs = plt.subplots(nrows=2)
    sns.histplot(
        data[label], 
        ax=axs[0]
    )
    sns.boxplot(
        x=data[label],
        ax=axs[1],
        showfliers=False
    )
    spacer = np.max(data[label]) * 0.05
    xmin = np.min(data[label]) - spacer
    xmax = np.max(data[label]) + spacer
    axs[0].set_xlim((xmin, xmax))
    axs[1].set_xlim((xmin, xmax))

    plt.subplots_adjust(hspace=0)
    fig.suptitle("Distribution of " + label)

#画出根据一列聚合的另一列的平均值
def draw_mean_lineplot(dis,val,df=training_data,thisbins=200):
    categories = pd.cut(df[dis], bins=thisbins)
    mids = [c.mid for c in categories]  
    df['distance_bin'] = mids
    mean_price = df.groupby('distance_bin')[val].mean()
    newdf=pd.DataFrame()
    newdf['mean_price']=mean_price
    newdf['distance_bin']=mean_price.index
    sns.lineplot(x='distance_bin',y='mean_price',data=newdf)
    plt.title("mean house price with the same "+dis)
    plt.show()

#画出线性分布图
def draw_lmplot(x_col,name,y_col="Median_House_Value",bins=100,ci=1):
    sns.lmplot(data = training_data, x = x_col, \
           y = y_col,x_bins=bins,x_ci=ci)
    plt.title("proportion of "+name+" against house value");
    
#绘制二元分布图 
def draw_jonitplot(x_col,name,y_col="Median_House_Value"):
    sns.jointplot(data = training_data, x = x_col, \
              y = y_col, \
              kind = "hex")
    plt.suptitle(name+" agginst value")

数据过滤

1
2
3
4
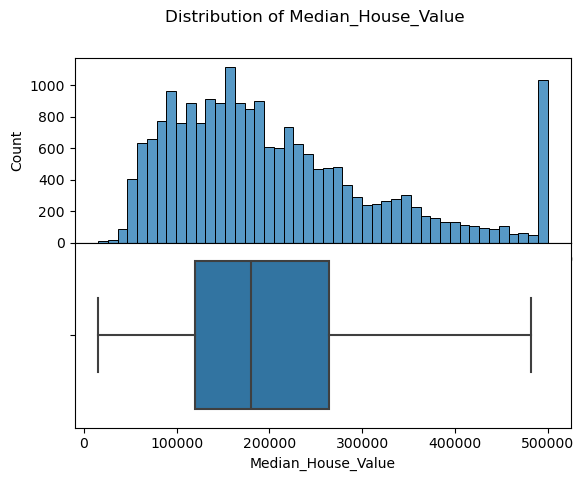
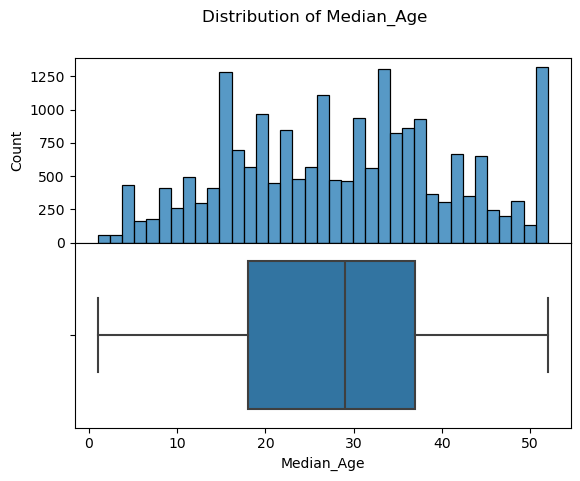
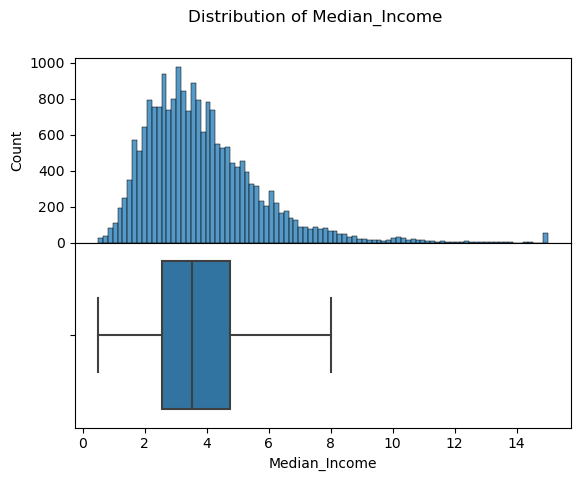
#观察数据分布
plot_distribution(training_data, label='Median_House_Value')
plot_distribution(training_data, label='Median_Age');
plot_distribution(training_data, label='Median_Income');
png
png
png

可以看到收入和售价数据的右侧末端比较不合理，应该过滤

1
2
3
4
training_data=remove_outliers(training_data,'Median_Income',0,8)
training_data=remove_outliers(training_data,'Median_House_Value',0,400000)
training_data=remove_outliers(training_data,'Distance_to_coast',0,70000)
training_data=remove_outliers(training_data,'Households',0,1500)
1
training_data.describe()
Median_House_Value Median_Income Median_Age Tot_Rooms Tot_Bedrooms Population Households Latitude Longitude Distance_to_coast Distance_to_LA Distance_to_SanDiego Distance_to_SanJose Distance_to_SanFrancisco
count 14651.000000 14651.000000 14651.000000 14651.000000 14651.000000 14651.000000 14651.000000 14651.000000 14651.000000 14651.000000 1.465100e+04 1.465100e+04 14651.000000 14651.000000
mean 199561.517917 3.696580 29.953996 2356.678657 496.034742 1367.255341 468.929561 35.372597 -119.555017 21259.751408 2.490542e+05 3.721187e+05 359123.874456 397236.235539
std 79310.711796 1.419884 12.191439 1425.953928 287.919292 814.994880 266.065608 2.077014 2.063217 16562.862059 2.475190e+05 2.905277e+05 226985.441402 262135.238533
min 14999.000000 0.499900 1.000000 11.000000 3.000000 3.000000 3.000000 32.540000 -124.350000 120.676447 4.205891e+02 4.849180e+02 569.448118 456.141313
25% 140600.000000 2.625000 20.000000 1410.000000 296.000000 816.000000 286.000000 33.880000 -121.890000 8077.199272 2.631262e+04 1.550810e+05 88700.495102 92070.783507
50% 187500.000000 3.551100 31.000000 2053.000000 431.000000 1190.000000 412.000000 34.140000 -118.360000 17596.867293 1.385490e+05 1.872540e+05 484362.783196 552023.712780
75% 252000.000000 4.625000 38.000000 2968.000000 631.000000 1725.000000 595.000000 37.690000 -117.980000 28063.195081 5.221622e+05 7.009827e+05 519935.107297 587792.558476
max 399400.000000 7.988700 52.000000 12837.000000 2219.000000 8733.000000 1499.000000 41.950000 -114.550000 69995.382339 1.018260e+06 1.196919e+06 836762.678210 903627.663298

数据分析——寻找与房屋价格有线性关系的列

可视化房屋价格与距离远近的关系

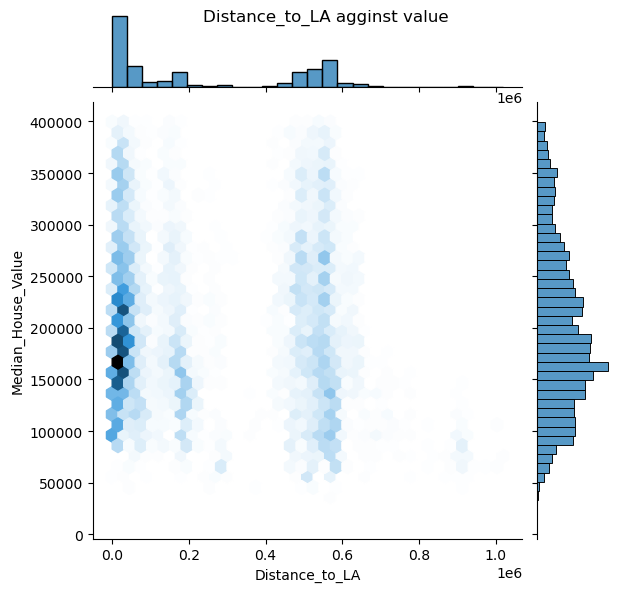
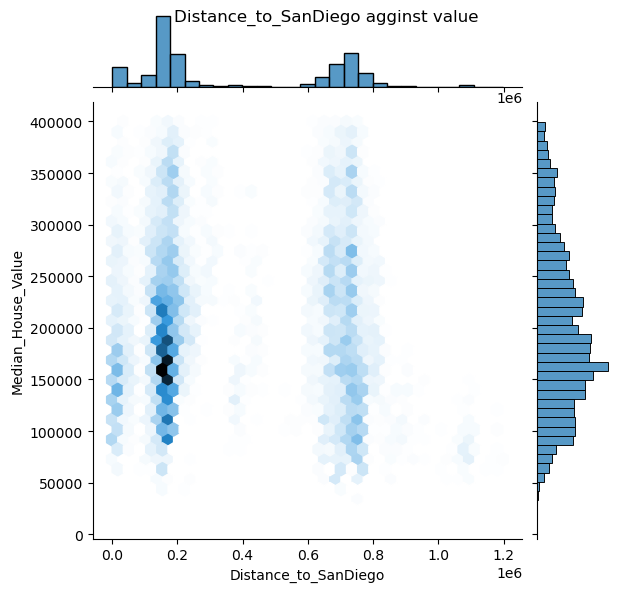
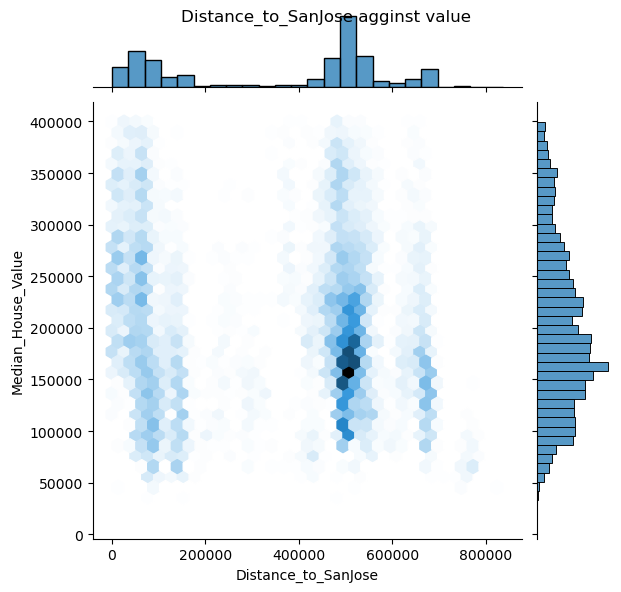
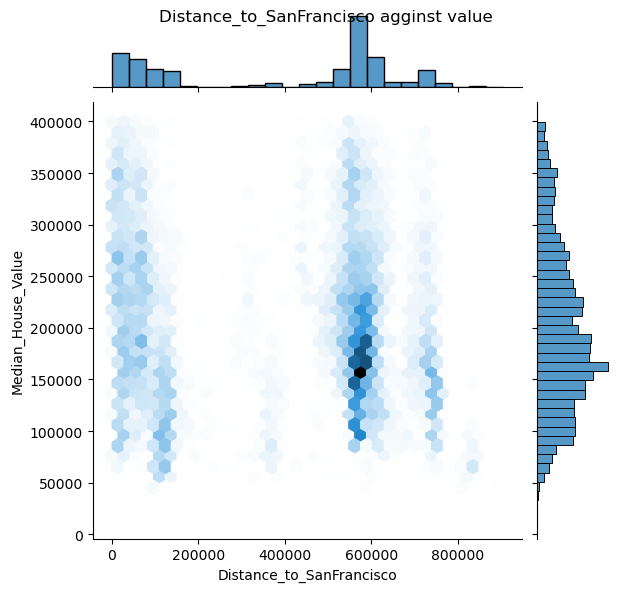
1
2
3
places=['Distance_to_coast', 'Distance_to_LA',
       'Distance_to_SanDiego', 'Distance_to_SanJose',
       'Distance_to_SanFrancisco']
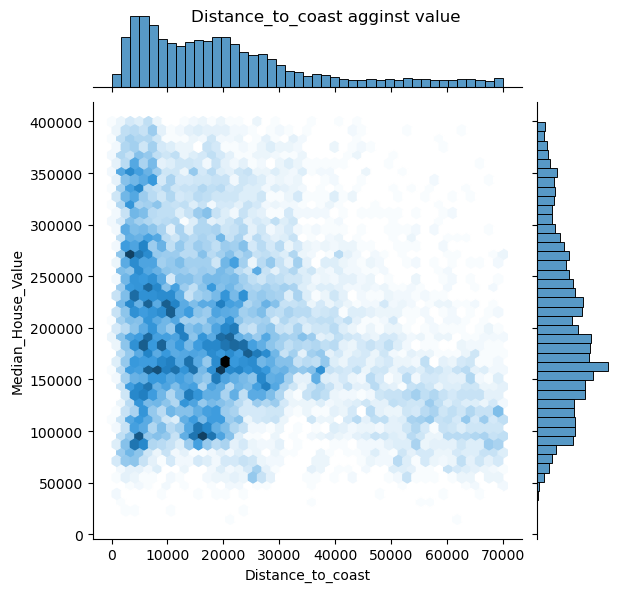
1
2
for pla in places:
    draw_jonitplot(x_col=pla,name=pla)
png
png
png
png
png

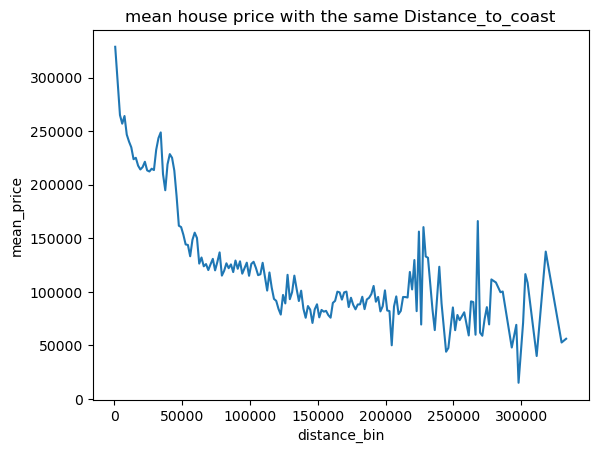
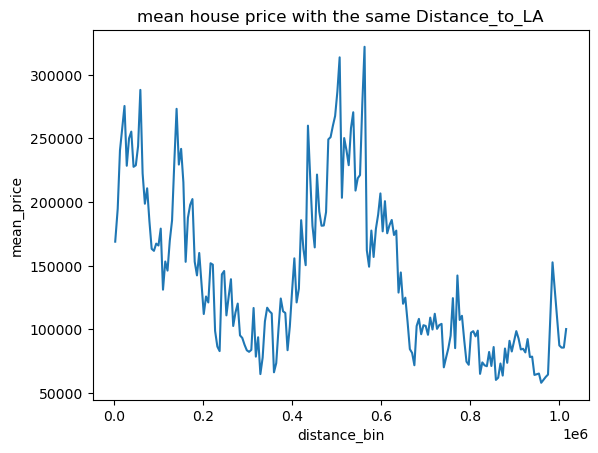
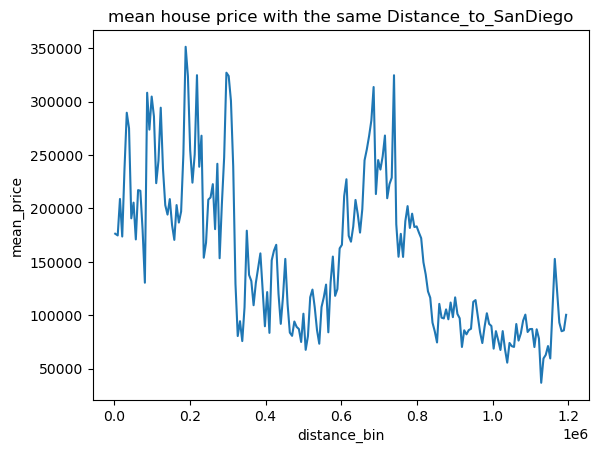
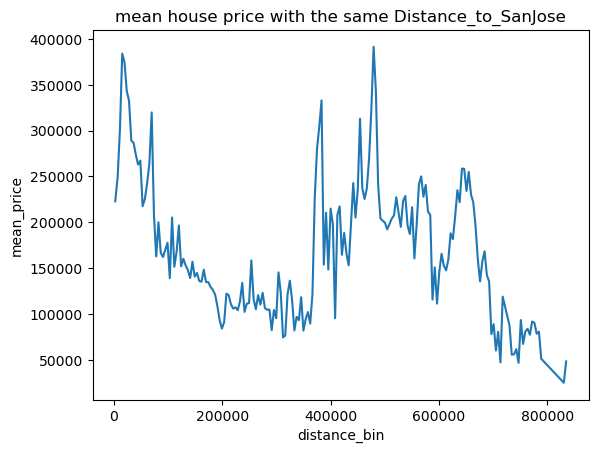
可以看出其中只有距海岸线距离似乎与房价有关系

用更直观的折线图表示平均房价与海岸线与城市距离关系

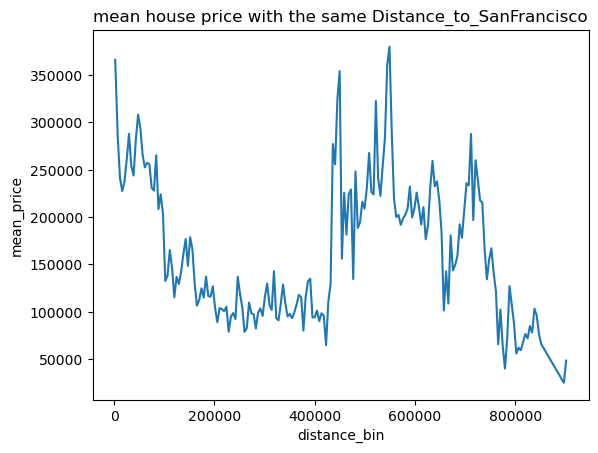
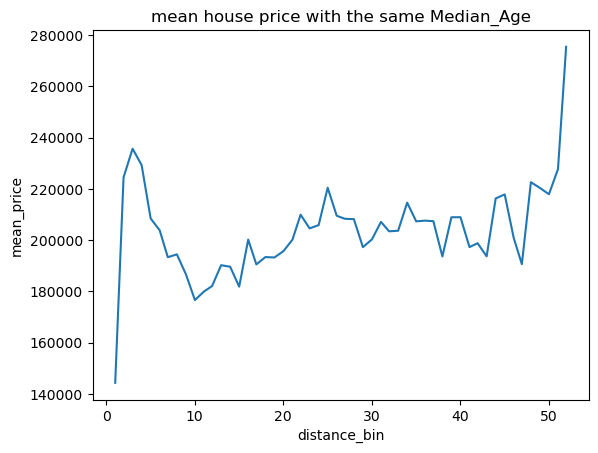
1
2
for pla in places:
    draw_mean_lineplot(dis=pla,val='Median_House_Value')
png
png
png
png
png

根据可视化发现，只有海岸线距离与房价有类似线性关系

房屋数和卧室数与房价是否相关

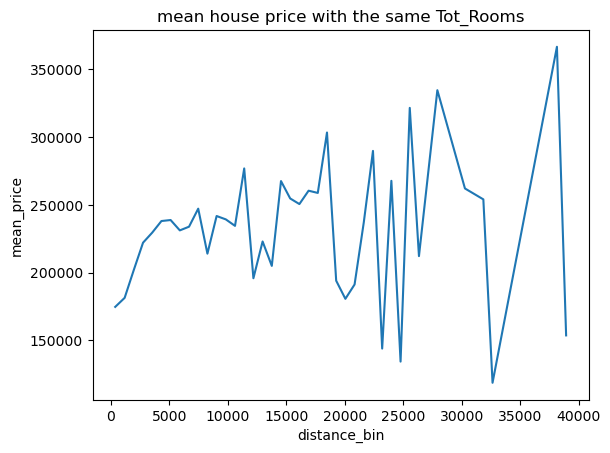
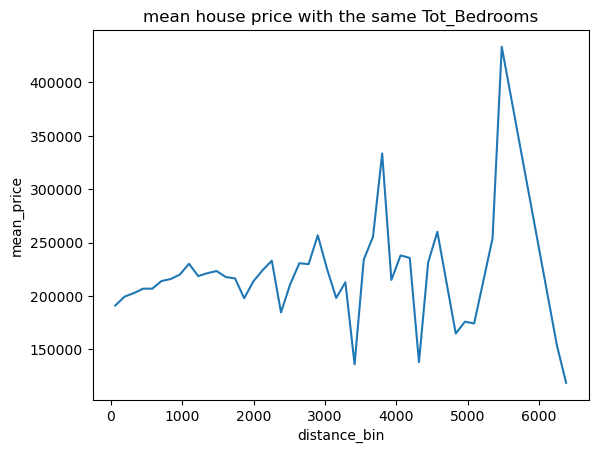
1
2
draw_mean_lineplot(dis='Tot_Rooms',val='Median_House_Value',thisbins=50)
draw_mean_lineplot(dis='Tot_Bedrooms',val='Median_House_Value',thisbins=50)
png
png

可以看出单独两列和房价都无明显关系

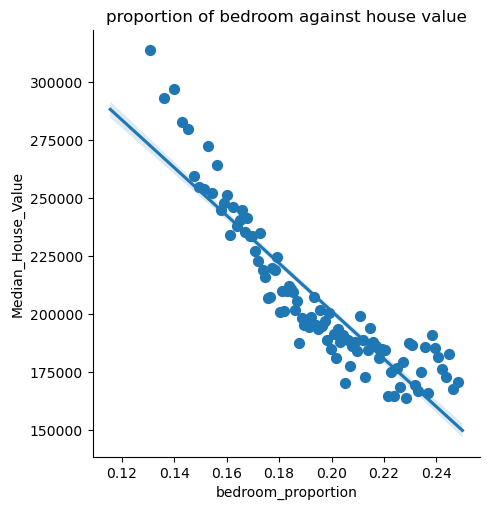
1
2
3
training_data['bedroom_proportion'] =training_data['Tot_Bedrooms'] / training_data['Tot_Rooms']
training_data=remove_outliers(training_data,'bedroom_proportion',0,0.25)
draw_lmplot(x_col='bedroom_proportion',name='bedroom')
png

两者比例和房价近似线性有关

和房屋年龄关系

1
draw_mean_lineplot(dis='Median_Age',val='Median_House_Value',thisbins=500)
png

可以看出和年龄没有明显关系

和家庭平均人口数的关系

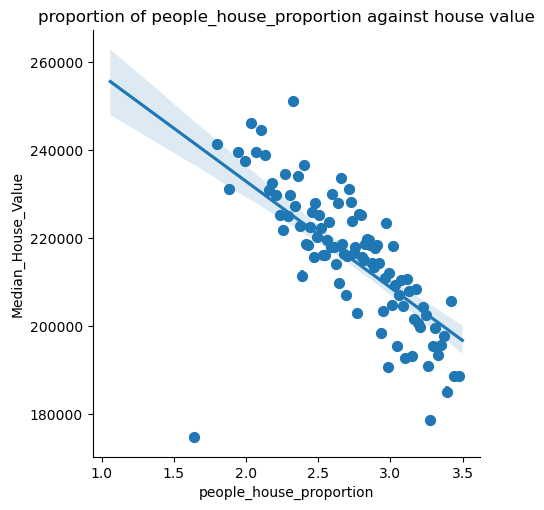
1
2
3
training_data['people_house_proportion'] =training_data['Population'] / training_data['Households']
training_data=remove_outliers(training_data,'people_house_proportion',0,3.5)
draw_lmplot(x_col='people_house_proportion',name='people_house_proportion')
png
1
training_data['people_house_proportion'].describe()
count    9213.000000
mean        2.722022
std         0.422372
min         1.060606
25%         2.432647
50%         2.740845
75%         3.044444
max         3.499266
Name: people_house_proportion, dtype: float64

可以看出和家庭平均人数有近似线性关系

与中位数收入的关系

1
draw_lmplot(x_col='Median_House_Value',name='Median_House_Value',ci=95)
png

可以看出和中位数收入线性有关

验证——相关性可视化

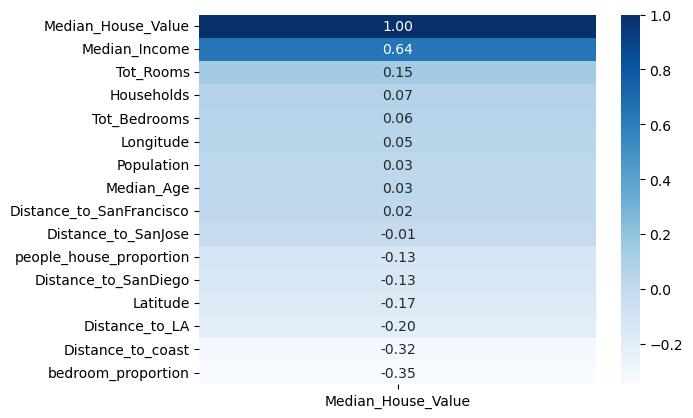
1
2
3
correlation = training_data.corr()['Median_House_Value'].sort_values(ascending = False).to_frame()
sns.heatmap(correlation, annot = True, cmap = 'Blues', fmt = '.2f')

<Axes: >
png

建立模型

由于数据呈现出较为标准的线性关系，选取了线性回归，决策树，随机森林，k近邻回归等回归模型，这些模型适合处理线性数据关系，并且其原理和训练方法容易理解。 缺点则是都是比较简单的模型，因此准确度不算特别理想，也不适宜处理关系复杂的数据

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#用到的辅助函数：

#划分数据为valid和train
def divide_datas(train,valid,list):
    X_train = train[list]
    y_train = train[['Median_House_Value']]
    X_valid = valid[list]
    y_valid = valid[['Median_House_Value']]
    return X_train,y_train,X_valid,y_valid

#把series转换成dataframe
def series_to_df(predict):
    predictions_series = pd.Series(predict[:,0])
    predictions_df = predictions_series.to_frame()
    predictions_df=predictions_df.rename(columns={0: 'house_value'})
    return predictions_df
    
#把n*1的series转换成1*n的series
def to_series(predict):
    s = pd.Series(predict)
    df = s.to_frame()
    return df.values

1
2
3
4
5
6
7
train_m1, valid_m1 = train_val_split(training_data)
train_m2, valid_m2 = train_val_split(training_data)
features=['Median_Income','Distance_to_coast','bedroom_proportion','people_house_proportion']
#模型1
X_train_m1,y_train_m1,X_valid_m1,y_valid_m1 = divide_datas(train_m1,valid_m1,['Median_Income'])
#模型2
X_train_m2,y_train_m2,X_valid_m2,y_valid_m2 = divide_datas(train_m2,valid_m2,features)

建立线性模型

\[ \hat{y}_i = \theta_0 + \theta_1 x_i \]

建立线性回归模型，并可视化预测值的分布与实际分布比较

1
2
3
4
5
6
7
8
9
from sklearn import linear_model as lm
linear_model_m1 = lm.LinearRegression()
linear_model_m2 = lm.LinearRegression()
# Fit the 1st model
linear_model_m1.fit(X_train_m1, y_train_m1)
# Compute the fitted and predicted values for 1st model
y_predicted_m1 = linear_model_m1.predict(X_valid_m1)
predictions_df=series_to_df(y_predicted_m1)

1
2
3
linear_model_m2.fit(X_train_m2, y_train_m2)
y_fitted_m2 = linear_model_m2.predict(X_train_m2)
y_predicted_m2 = linear_model_m2.predict(X_valid_m2)
1
linear_model_m1.score(X_train_m1, y_train_m1)
0.405456747259772
1
linear_model_m2.score(X_train_m2, y_train_m2)
0.5238399282191235

可以看出使用更多特征列的模型二有更好的性能

主成分分析（PCA）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from sklearn.decomposition import PCA
linear_model_m3 = lm.LinearRegression()
train_m3, valid_m3 = train_val_split(training_data)
#模型3
X_train_m3,y_train_m3,X_valid_m3,y_valid_m3 = divide_datas(train_m3,valid_m3,features)
#对特征数据进行奇异值分解
pca = PCA(n_components=4)
pca.fit(X_train_m3)
principal_components = pca.transform(X_train_m3)

pca.fit(X_valid_m3)
principal_components_valid = pca.transform(X_valid_m3)
#用PCA处理后的数据来训练模型
linear_model_m3.fit(principal_components, y_train_m3)

# 计算模型预测的数据
y_fitted_m3 = linear_model_m3.predict(principal_components)
y_predicted_m3 = linear_model_m3.predict(principal_components_valid)
1
2
linear_model_m3.score(principal_components, y_train_m3)

0.5185359815322779

正则化

1
2
3
4
5
#l1正则化模型
lasso_model = lm.Lasso(alpha=3)
lasso_model.fit(X_train_m3, y_train_m3)
y_predicted_lasso = lasso_model.predict(X_valid_m3)
y_predicted_lasso=to_series(y_predicted_lasso)
1
2
3
4
#l2正则化模型
ridge_model = lm.Ridge(alpha=3)
ridge_model.fit(X_train_m3, y_train_m3)
y_predicted_ridge = ridge_model.predict(X_valid_m3)
1
ridge_model.score(X_train_m3, y_train_m3)
0.5177135759219753
1
lasso_model.score(X_train_m3, y_train_m3)
0.5185322538476318

决策树模型

1
2
3
4
5
6
#分类模型
from sklearn import tree
decision_tree_model = tree.DecisionTreeClassifier(max_depth=50,min_samples_split=4)
decision_tree_model = decision_tree_model.fit(X_train_m3, y_train_m3)
y_predicted_tree=decision_tree_model.predict(X_valid_m3)
y_predicted_tree=to_series(y_predicted_tree)
1
2
3
4
5
#回归模型
decision_tree_model_regression = tree.DecisionTreeRegressor(criterion='absolute_error',min_samples_split=3)
decision_tree_model_regression = decision_tree_model_regression.fit(X_train_m3, y_train_m3)
y_predicted_tree_regression=decision_tree_model_regression.predict(X_valid_m3)
y_predicted_tree_regression=to_series(y_predicted_tree_regression)
1
decision_tree_model.get_depth()
50
1
2
3
4
5
#随机森林回归模型
from sklearn.ensemble import RandomForestRegressor
forest_model = RandomForestRegressor(criterion='absolute_error',max_depth=50,random_state=0,min_samples_leaf=3,n_jobs=4)
forest_model = forest_model.fit(principal_components,y_train_m3)

1
2
y_predicted_forest=forest_model.predict(principal_components_valid)
y_predicted_forest=to_series(y_predicted_forest)

k近邻回归

1
2
3
4
from sklearn.neighbors import KNeighborsRegressor
KE_model=KNeighborsRegressor(n_neighbors=2,weights='distance') 
KE_model=KE_model.fit(X_train_m3,y_train_m3)
y_predicted_ke=KE_model.predict(X_valid_m3)

模型评估

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#用到的辅助函数：
#误差分析
def rmse(predicted, actual):
    return np.sqrt(np.mean((actual - predicted)**2))
def mae(predicted,actual):
    return np.mean(np.abs(predicted - actual))
def accuracy(preditcted,actual,num=500):
    return (abs(preditcted - actual)<=num).mean().mean()

#用以上三个误差评估函数评估预测数据
def evaluate_model(predicted,valid,num=500):
    rmse_val = rmse(predicted, valid)
    mae_val = mae(predicted,valid)
    accuracy_val = accuracy(predicted,valid,num)
    return {'rmse': rmse_val, 'mae': mae_val, 'accuracy' : accuracy_val}

#计算出最后结果，存储到df
def make_result(predicts,df):
    for predict in predicts:
        df.loc[len(df)] = evaluate_model(predict, y_valid_m3,10000)
    return df

#画出误差散点图
def scatter_plot(predict,actual,name):
    residuals = abs(predict - actual)
    plt.scatter(predict, residuals, alpha=0.5, s=3)
    plt.xlabel('Sale Price') 
    plt.ylabel('Residuals')
    plt.title('Residuals vs. Sale Price for '+name)
    ax=axs[1]
    plt.show()

#画出预测结果和验证集的分布图
def two_x_histplot(df1,df2,col1,col2):
    min_value = min(df1[col1].min(), df2[col2].min())
    max_value = max(df1[col1].max(), df2[col2].max())
    bins = np.linspace(min_value, max_value, 50)
    sns.histplot(data=df1, x=col1, alpha=0.5,bins=bins,color='#66ccff')
    sns.histplot(data=df2, x=col2, alpha=0.3,bins=bins,color='y')
    ax=axs[0]
    plt.show()

1
2
3
4
5
6
7
8
#最终结果汇总
results = pd.DataFrame(columns=['rmse', 'mae', 'accuracy']) 
results.loc[len(results)] = evaluate_model(y_predicted_m1, y_valid_m1,10000)
results.loc[len(results)] = evaluate_model(y_predicted_m2, y_valid_m2,10000)
pres=[y_predicted_m3,y_predicted_lasso,y_predicted_ridge,y_predicted_tree,y_predicted_tree_regression,y_predicted_forest,y_predicted_ke]
results=make_result(pres,results)
results.index=['lm_model1','lm_model2','lm_pca_model3','lasso','ridge','tree','tree_regression','forest_regression','K_neighbours']
results
rmse mae accuracy
lm_model1 60922.482902 48571.055228 0.135648
lm_model2 56846.626574 43979.354330 0.160608
lm_pca_model3 55342.558354 43704.366177 0.154097
lasso 55311.818220 43551.728305 0.150841
ridge 55434.380284 43656.940158 0.150841
tree 77547.042415 58941.074335 0.141617
tree_regression 73484.094196 56195.496473 0.127509
forest_regression 52955.981209 40886.882257 0.170917
K_neighbours 74706.010594 52427.281809 0.204558 
1
2
3
4
5
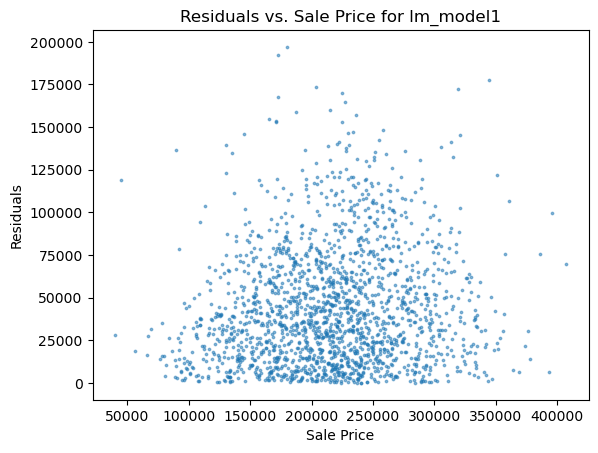
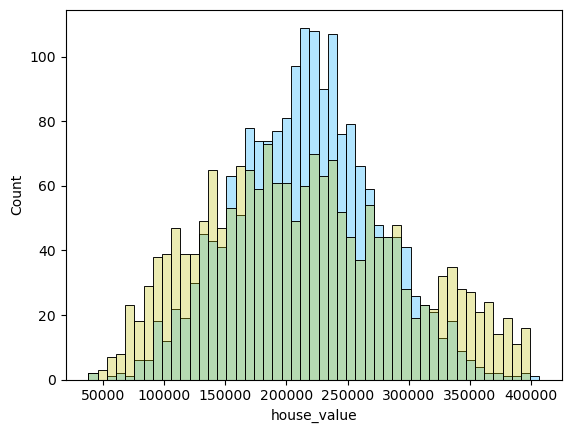
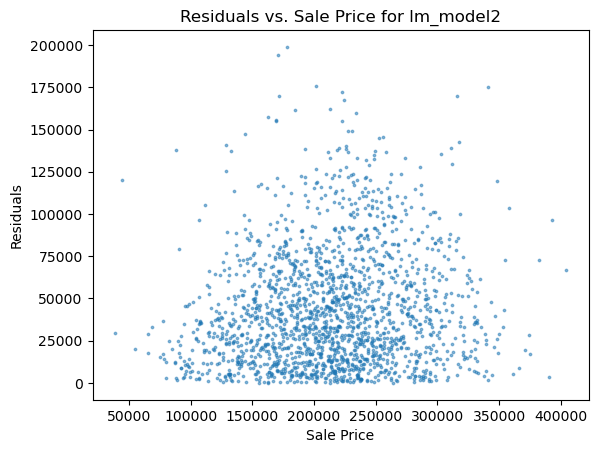
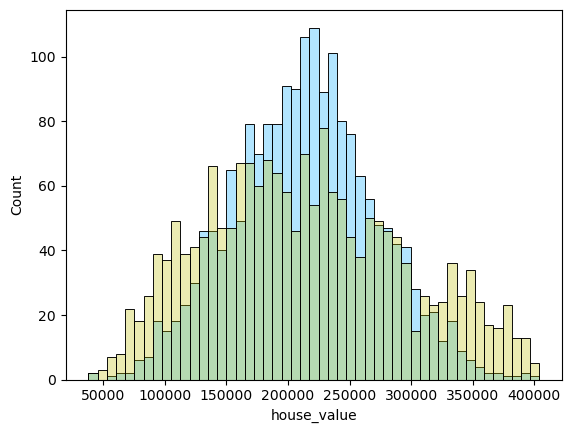
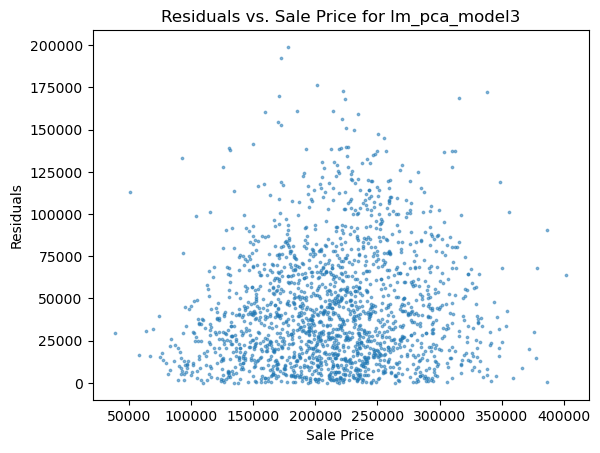
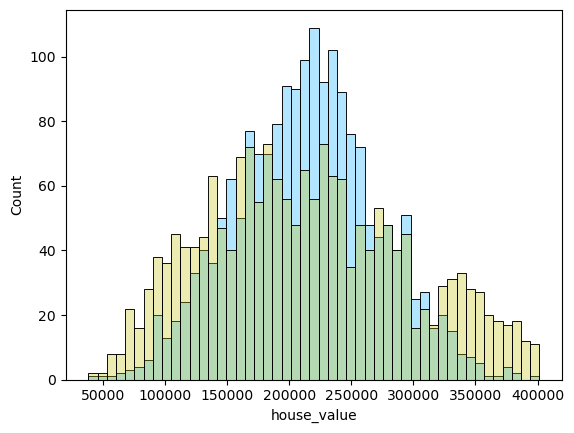
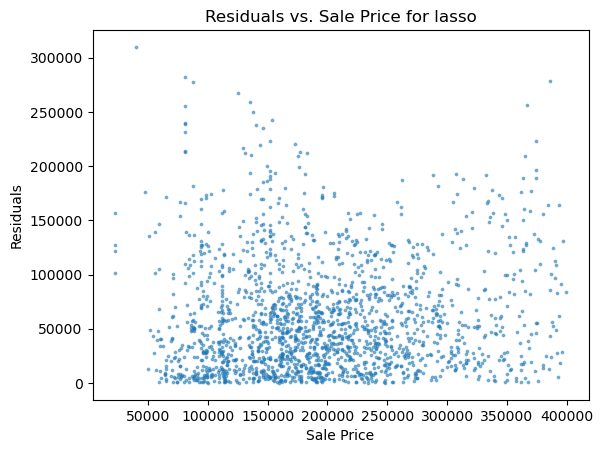
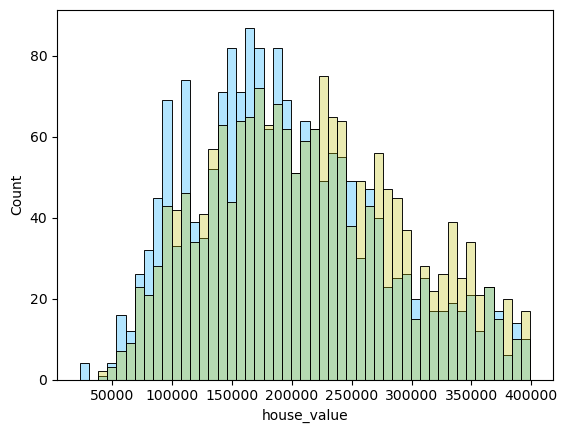
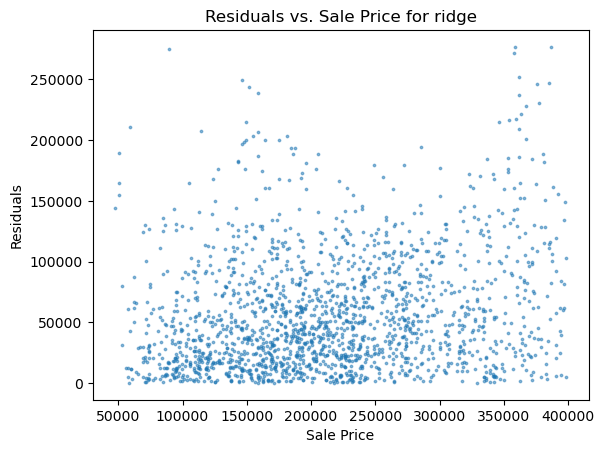
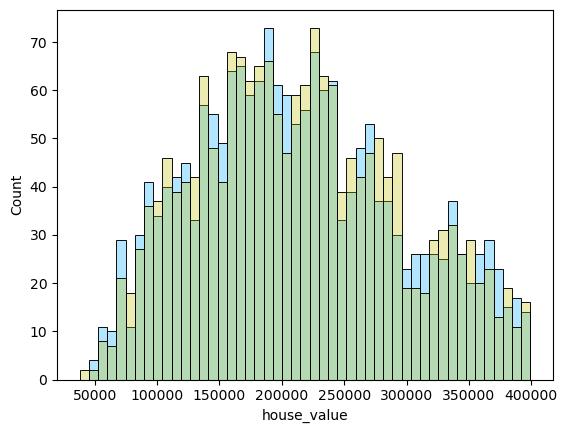
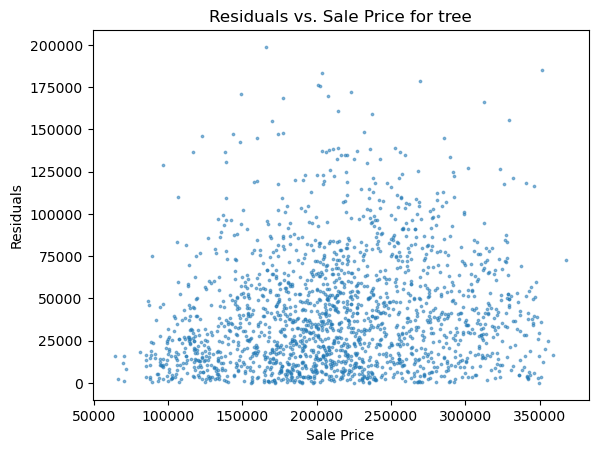
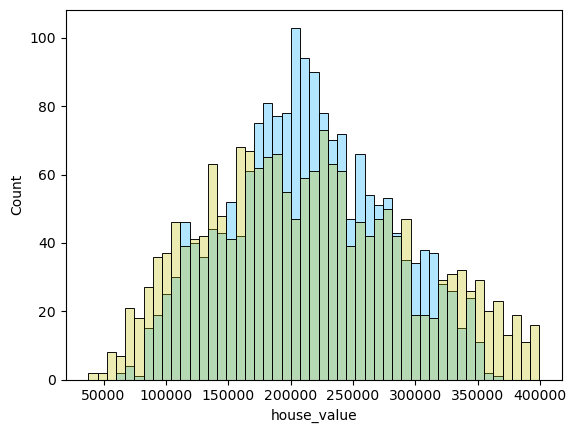
6
#误差可视化
for i in range(len(pres)):
    names=['lm_model1','lm_model2','lm_pca_model3','lasso','ridge','tree','tree_regression','forest_regression','K_neighbours']
    scatter_plot(pres[i],y_valid_m3,names[i])
    two_x_histplot(series_to_df(pres[i]),y_valid_m3,"house_value","Median_House_Value")
    plt.show()
png
png
png
png
png
png
png
png
png
png
png
png
png
png

交叉验证

1
2
3
4
5
6
7
8
9
from sklearn.model_selection import cross_val_predict
def cross_validation(mls,is_series):
    result_df=pd.DataFrame(columns=['rmse', 'mae', 'accuracy']) 
    for i in range(len(models)):
        predicted=cross_val_predict(mls[i], X_train_m3, y_train_m3, cv=10,n_jobs=-1)
        if (is_series[i]): predicted=to_series(predicted)
        result_df.loc[len(result_df)]=evaluate_model(predicted, y_train_m3,10000)
    return result_df

1
2
3
4
5
linear_model_m1 = lm.LinearRegression()
models=[linear_model_m3,lasso_model,ridge_model,decision_tree_model,decision_tree_model_regression,forest_model,KE_model]
tf=[0,1,0,1,1,1,0]
cross_results=cross_validation(models,tf)
cross_results.index=['lm_model','lasso','ridge','tree','tree_regression','forest_regression','K_neighbours']
1
cross_results
rmse mae accuracy
lm_model 55984.041030 43744.485025 0.150611
lasso 55984.270526 43748.196798 0.151018
ridge 56032.724551 43836.923361 0.149661
tree 76236.606876 58051.316147 0.139620
tree_regression 75482.497313 56896.289009 0.147083
forest_regression 53620.108361 40894.203324 0.174763
K_neighbours 76776.253905 55102.977787 0.192130