研distance——数据结构部分
概念
数据
数据:信息的载体,在计算机中是符号的集合数据元素:数据的基本单位,一个整体,由一些不可分割的数据项组成,例如一个学生档案数据对象:有相同性质的数据元素集合,是数据的子集数据类型:数据值的类型,和对这个类型特定操作的集合数据结构:相互之间存在特殊关系的数据元素的集合,这种特殊关系就是所谓的结构。
数据结构包括三个方面
逻辑结构(数据的逻辑关系,和怎么存储在计算机中无关)存储结构(数据在计算机中的表示)顺序存储:元素存储在相邻的地址间,不需要额外索引,可以随机读写,但容易产生外部碎片链式存储:每个元素不仅存储值,还存储指向下一个元素的指针,不会产生碎片,但占用空间较大索引存储:建立一个外部索引表,利用索引表对数据进行读写,需要额外空间并管理表格散列存储:对每个元素用一个哈希函数计算其存储的地址,需要恰当的哈希函数
数据的运算
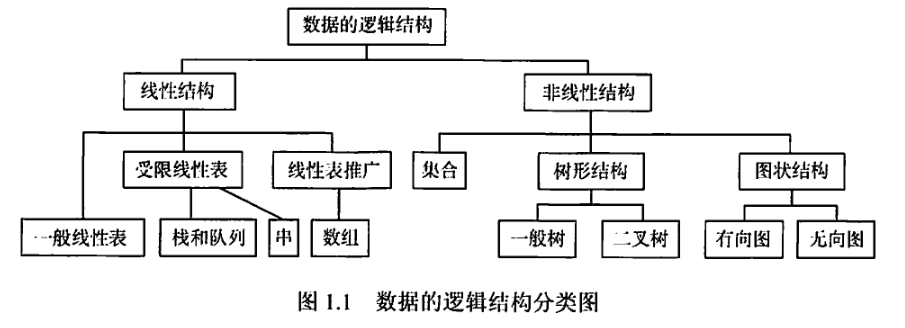
ADT(抽象数据类型)构成一个完整的数据结构定义
算法
算法是对指定输入的一系列指令 特性:
有穷性,执行时间和指令次数有穷确定性,指令有确定的含义,相同输入输出一定相同可行性,指令都是以及明确实现有定义的输入:有零个或者多个输入输出:有一个或以上的输出
需要实现的目标:正确,可读,健壮(对于非法数据,也输出可控),效率
复杂度:略
线性表
定义:有相同数据类型的n个数据元素的有限序列,元素直接存在前后关系,且只能线性前后排列,其中的元素都是数据元素,类型相同
类别:逻辑结构,而非顺序表链表等存储结构
基本操作:
- 初始化
- 按值查找
- 按位查找
- 删除元素
- 输出(如输出到ostream)
- 求表长
- 销毁
- 判空
顺序表
定义:线性表的顺序存储是顺序表,用连续的地址存储表内元素,让逻辑顺序和物理顺序相同
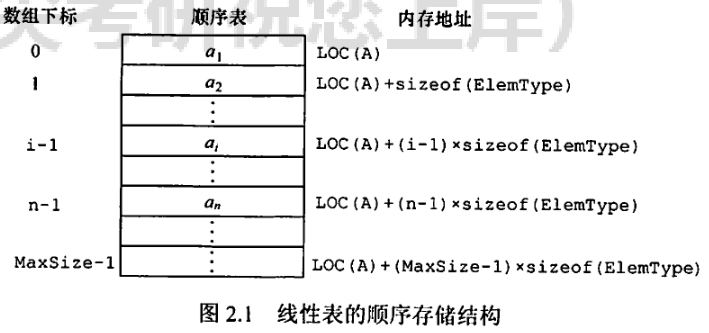
1
2
3
4
5
6
7
typedef struct{
ElemType* data[Maxsize]; //顺序表的元素
int length; //顺序表的当前长度
}SeqList; //顺序表的类型定义
L.data=new ElemType[InitSize]; //动态分配
- 插入操作
1 | bool ListInsert(sqList &L, int i, ElemType e) { |
平均时间分析:
\(\sum_{i=1}^{n+1}p_{i}(n-i+1)=\sum_{i=1}^{n+1}{\frac{1}{n+1}}(n-i+1)={\frac{1}{n+1}}\sum_{i=1}^{n+1}(n-i+1)={\frac{1}{n+1}}{\frac{n(n+1)}{2}}={\frac{n}{2}}\)
- 删除操作
平均时间分析:
\(\sum_{i=1}^{n}p_{i}(n-i)=\sum_{i=1}^{n}{\frac{1}{n}}(n-i)={\frac{1}{n}}\sum_{i=1}^{n}(n-i)={\frac{1}{n}}{\frac{n(n-1)}{2}}={\frac{n-1}{2}}\)
1 | bool ListDelete(SqList &L,int i,Elemtype &e) { |
- 按值查找
1 | int LocateElem(SqList L, ElemType e) { |
平均情况:假设pi是(pi=1/n)是查找的元素在第i(1<=i<=L.length)个位置上的概率
\(\sum_{i=1}^{n}p_{i}\times i=\sum_{i=1}^{n}{\frac{1}{n}}\times i={\frac{1}{n}}{\frac{n(n+1)}{2}}={\frac{n+1}{2}}\)
- 线性表的顺序存储结构是一种随机存取的存储结构,此处的顺序存取指的是只能线性遍历的数据结构,而顺序表可以随机存取
- 本书中的时间复杂度默认指渐进时间复杂度,即n默认趋近正无穷,而不是常数
时间O(n),空间O(1)的删除表内一个值的算法:
1 | void del(SqList& L, ElemType x) { |
练习代码:
1 |
|
链式表示
1 | typedef struct LNodef { //定义单链表结点类型 |
一般会用一个头结点指向单链表,头结点的数据没有意义,空链表时指针是一个空指针
头指针指向单链表的第一个节点,对有头指针的链表就是指向头结点
头结点的优点:
- 所有数据节点都可以用相同的办法处理
- 由于有
头节点,头指针不会是一个空指针,空表和非空表也可以统一处理
基本操作
c++实现的一些基本操作: 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
using namespace std;
struct LNode { // 定义单链表结点类型
int data = 0; // 数据域
struct LNode* next = NULL; // 指针域
};
struct DoubleLNode { // 定义双链表结点类型
int data = 0; // 数据域
struct DoubleLNode* prior = NULL; // 指针域
struct DoubleLNode* next = NULL; // 指针域
};
typedef LNode* LinkList;
typedef DoubleLNode* DLinkList;
// 遍历且打印链表,略过头结点
void print_linklist(LinkList L) {
L = L->next;
int i = 1;
while (L != NULL) {
cout << i++ << ":" << L->data << endl;
L = L->next;
}
}
// 遍历且打印循环单链表,略过头结点
void print_loop_linklist(LinkList L) {
LinkList head = L;
L = L->next;
if (L == NULL) return;
int i = 1;
while (L != head) {
cout << i++ << ":" << L->data << endl;
L = L->next;
}
}
//遍历且打印循环双链表
void print_linklist(DLinkList L) {
DLinkList head = L;
L = L->next;
int i = 1;
while (L != head) {
cout << i++ << ":" << L->data << endl;
L = L->next;
}
}
//根据数组以尾插法生成链表
LinkList build_nodelist(LinkList& L, int lst[], int length) {
LNode* r = L;
for (int i = 0; i < length; i++) {
LNode* s = new LNode; // 创建新结点
s->data = lst[i];
r->next = s;
r = s;
}
r->next = NULL;
return L;
}
//根据数组以尾插法生成循环单链表
LinkList build_loop_list(LinkList& L, int lst[], int length) {
LNode* r = L;
for (int i = 0; i < length; i++) {
LNode* s = new LNode; // 创建新结点
s->data = lst[i];
r->next = s;
r = s;
}
r->next = L;
return L;
}
//根据数组以尾插法生成循环双链表
DLinkList build_loop_double_list(DLinkList& L, int lst[], int length) {
DoubleLNode* r = L;
for (int i = 0; i < length; i++) {
DoubleLNode* s = new DoubleLNode; // 创建新结点
s->data = lst[i];
s->prior = r;
r->next = s;
r = s;
}
L->prior = r;
r->next = L;
return L;
}
//头插法生成链表,即遍历顺序和输入顺序相反
LinkList List_HeadInsert(LinkList& L) {
LNode* s;
int x;
cout << "输入结点的值:" << endl;
cin >> x; // 输入结点的值
while (x != 9999) { // 输入9999表示结束
s = new LNode; // 创建新结点
s->data = x;
s->next = L->next;
L->next = s; // 将新结点插入表中,L为头指针
cout << "输入结点的值:" << endl;
cin >> x; // 输入结点的值
}
return L;
}
//尾插法生成链表,即遍历顺序和输入顺序一致
LinkList List_TailInsert(LinkList& L) {
int x;
LNode* r = L;
cout << "输入结点的值:" << endl;
cin >> x; // 输入结点的值
while (x != 9999) {
LNode* s = new LNode;
s->data = x;
r->next = s;
r = s; // r指向新的表尾结点
cout << "输入结点的值:" << endl;
cin >> x; // 输入结点的值
}
r->next = NULL; // 尾结点指针置空
return L;
}
//按值查找节点,不存在返回NULL
LNode* LocateElem_byval(LinkList L, int e) {
LNode* p = L->next;
while (p != NULL && p->data != e) // 从第1个结点开始查找data域为e的结点
p = p->next;
return p; // 找到后返回该结点指针,否则返回NULL
}
//按序号定位结点,如果越界返回NULL
LNode* LocateElem_byno(LinkList L, int i) {
if (i < 1)
return NULL;
int j = 1;
LNode* p = L->next;
while (p != NULL && j < i) {
p = p->next;
j++;
}
return p;
}
//插入删除略,删除时要用delete回收内存!!!
LinkList merge_list(LinkList head, LinkList tail) {
LinkList temp = head;
while (temp->next != NULL) temp = temp->next;
temp->next = tail->next;
return head;
}
循环单链表表尾结点*r的next域指向L,故表中没有指针域为NULL的结点,判空条件是当前节点是否等于头指针
有时对循环单链表不设头指针而仅设尾指针,若设的是头指针,对在表尾插入元素需要O(n)的时间复杂度,而若设的是尾指针r,r->next即为头指针,对在表头或表尾插入元素都只需要O(1)的时间复杂度
循环双链表中,头结点的prior指针还要指向表尾结点,为空时,头结点的前后指针都指向自己
静态链表借助数组来描述线性表的链式存储结构,其指针是结点的相对地址(数组下标),又称游标,需要预先分配一块连续的内存空间 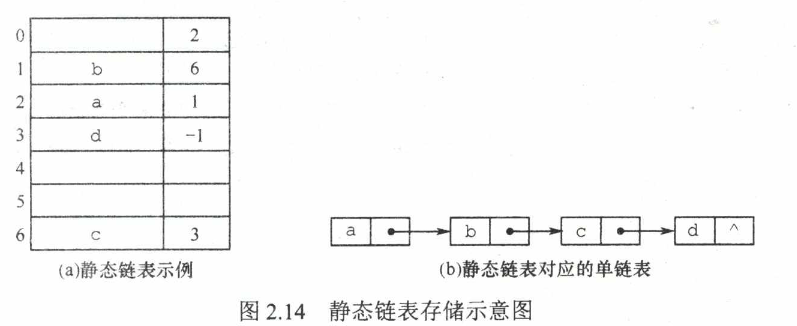
1
2
3
4
5
typedef struct{
ElemType data;
int next;
} SLinkList[MaxSize];
顺序表和链表的比较:
- 顺序表可以顺序存取,也可以随机存取,链表只能从表头顺序存取元素
- 采用顺序存储时,逻辑上相邻的元素,对应的物理存储位置也相邻。而采用链式存储时,逻辑上相邻的元素,物理存储位置不一定相邻
- 顺序存储需要连续空间,一旦溢出,动态分配成本较大,而链表更灵活,可以一直O(1)时间添加元素
- 链表存储密度更小,必然小于1,且实现更复杂
练习代码: 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
// 1.递归删除不带头结点链表值为x的节点
void del_by_val(LinkList& L, const int& x) {
if (L == NULL) return;
if (L->data == x) {
LinkList l = L;
L = L->next; // 这里L为调用该函数的外层L->next,故这里实现了L->next=L-next->next
delete l;
del_by_val(L, x);
}
else
del_by_val(L->next, x);
}
// 2.在带头结点的单链表L中,删除所有值为x的结点
void del_by_val_withhead(LinkList p, int x) { // p是先驱节点,最初是头结点
LinkList q = p->next;
while (q != NULL) { // 循环检查后继结点的值是否是x
if (q->data == x) {
p->next = q->next;
LinkList temp = q;
q = p->next;
delete temp;
}
else {
p = p->next;
q = p->next;
}
}
}
// 3.带头结点的单链表从尾到头反向输出每个结点的值
void print_linklist_rev(LinkList L) {
if (L == NULL)
return;
else
print_linklist_rev(L->next);
cout << L->data << endl;
}
LinkList remove_head(LinkList head) {
if (head->next == NULL) return NULL;
return head->next;
}
// 4.在带头结点的单链表L中删除一个最小值结点(假设唯一)
void del_min_withhead(LinkList L) {
if (L->next == NULL) return;
LinkList prev = L;
L = L->next;
LinkList min_node, min_prev;
int min_val = INT16_MAX;
while (L != NULL) {
if (L->data < min_val) min_node = L, min_prev = prev, min_val = L->data;
prev = L;
L = L->next;
}
min_prev->next = min_node->next;
delete min_node;
cout << "删除的节点值为:" << min_val << endl;
}
//5.将带头结点的单链表就地逆置
LinkList rev_insite_withhead(LinkList L) {
LinkList head = L, temp; //暂存头结点
L = L->next;
LinkList p = L->next; //L和p分别是先驱后继节点
L->next = NULL;
while (p != NULL) {
temp = p->next; //暂存p之后的链表
p->next = L; //反转L和p
L = p;
p = temp;
}
head->next = L;
return head;
/*另一种解法
LNode* p, * r;
p = L->next;
L->next = NULL;
while (p != NULL) {
r = p->next;
p->next = L->next;
L->next = p;//将P结点插入到头结点之后
p = r;
}
return L;*/
}
/*6.插入排序带头结点的单链表L
1. 排序部分初始为头结点及其后续一个节点,未排序部分是head->next->next为首的链表
2. 取一个未排序节点,遍历找到插入位置
3. 插入节点,将leaft指向之前暂存的未排序部分首个结点
*/
void insertsort_list(LinkList L) {
LinkList leaft = L->next;//leaft是未排序部分的首个节点
LinkList remains = leaft->next;
leaft->next = NULL;
leaft = remains;
while (leaft != NULL) {
remains = leaft->next;
LinkList prev = L;
while (prev->next != NULL && leaft->data > prev->next->data) prev = prev->next;
//注意要先判断next是否为空,否则会访问空指针出现异常!!!
leaft->next = prev->next;
prev->next = leaft;
leaft = remains;
}
}
//7. 删除无序带头结点单链表介于[x,y]内的值
void del_val_inrange(LinkList L, int x, int y) {
LinkList p = L, q = L->next;
while (q != NULL) {
if (q->data < y && q->data >x) {
LinkList temp = q;
p->next = q->next;
delete temp;
q = p->next;
continue;
}
p = p->next;
q = q->next;
}
}
/*8.找出两个链表的公共结点
若有公共结点,则从其开始,两链表完全一致,因此必出现在距离尾部距离一致的地方
因此可以将较长的链表截断到较短链表长度,随后遍历寻找公共结点
*/
int len_of_list(LinkList L);
LinkList find_public_node(LinkList L1, LinkList L2) {
int len1 = len_of_list(L1->next);
int len2 = len_of_list(L2->next);
LinkList longer, shorter;
longer = (len1 > len2) ? L1->next : L2->next;
shorter = (len1 > len2) ? L2->next : L1->next;
longer = (len1 == len2) ? longer : LocateElem_byno(longer, abs(len1 - len2));
while (longer != NULL) {
if (longer == shorter) return longer;
longer = longer->next;
shorter = shorter->next;
}
return NULL;
}
int len_of_list(LinkList L) {
int len = 0;
while (L != NULL) {
len++;
L = L->next;
}
return len;
}
//9.按递增次序输出单链表中各结点的数据元素,并释放结点,就地算法
void print_and_del_sorted_list(LinkList& L) {
if (L->next == NULL) return;
LinkList iter = L->next->next, min = L->next, prev = min, prev_min = L;
while (iter != NULL) {
if (min->data > iter->data) min = iter, prev_min = prev;
prev = iter;
iter = iter->next;
}
prev_min->next = min->next;
cout << min->data << endl;
delete min;
print_and_del_sorted_list(L);
}
//10.将一个带头结点的单链表按奇偶分解成两个链表
pair<LinkList, LinkList> tear_list(LinkList L) {
int signal = 1;
LinkList L1head = new LNode, L2head = L;
LinkList q = L->next;
L->next = NULL;
while (q != NULL) {
LinkList temp = q->next;
if (signal == 1) {
signal = 0;
q->next = L1head->next;
L1head->next = q;
}
else {
signal = 1;
q->next = L2head->next;
L2head->next = q;
}
q = temp;
}
return make_pair(L1head, L2head);
}
//11.C= {a1, b1,...,an,bn}线性表,采用带头结点的单链表存放,设计一个就地算法,将其拆分为两个线性表,使得A = (a1 a2,,,an}, B= bn,,,b2,b1}
//即一个头插法,一个尾插法
pair<LinkList, LinkList> tear_list_rev(LinkList L) {
LinkList L1head = new LNode, L1tail = L1head, L2head = L;
LinkList node = L->next;
L2head->next = NULL;
int signal = 0;
while (node != NULL) {
LinkList temp = node->next;
if (signal == 0) {
signal = 1;
L1tail->next = node;
L1tail = node;
}
else {
signal = 0;
node->next = L2head->next;
L2head->next = node;
}
node = temp;
}
L1tail->next = NULL;
return make_pair(L1head, L2head);
}
//12.递增有序的线性表去除重复元素
void remove_samepart_list(LinkList L) {
LinkList prev = L->next, q = prev->next;
while (prev->next != NULL) {
q = prev->next;
if (prev->data == q->data) {
prev->next = q->next;
delete q;
continue;
}
prev = prev->next;
}
}
/*13.两个按元素值递增次序排列的单链表,归并为一个按元素值递增次序排列的单链表,不创造新节点
如果是递减版本,则需要使用头插法
*/
LinkList merge_and_sort(LinkList L1, LinkList L2) {
LinkList l1node = L1->next, l2node = L2->next, l1tail = L1;
L1->next = NULL;
while (l1node != NULL && l2node != NULL) {
LinkList temp;
if (l1node->data < l2node->data) {
l1tail->next = l1node;
l1tail = l1node;
l1node = l1node->next;
}
else {
l1tail->next = l2node;
l1tail = l2node;
l2node = l2node->next;
}
}
l1tail->next = (l1node == NULL) ? l2node : l1node;
delete L2;
return L1;
}
//14.两个递增有序单链表,用其公共元素产生一个新链表
LinkList build_list_from_public(LinkList L1, LinkList L2) {
LinkList prev1 = L1, prev2 = L2;
LinkList L3 = new LNode;
while (prev1->next != NULL && prev2->next != NULL) {
if (prev1->next->data == prev2->next->data) {
LinkList new_node = new LNode;
new_node->data = prev1->next->data;
new_node->next = L3->next;
L3->next = new_node;
prev1 = prev1->next;
prev2 = prev2->next;
}
else if (prev1->next->data < prev2->next->data) prev1 = prev1->next;
else prev2 = prev2->next;
}
return L3;
}
//15.两个链表分别表示两个集合,其元素递增排列,将其交集存放于A链表
LinkList list_intersection(LinkList L1, LinkList L2) {
LinkList prev1 = L1, prev2 = L2, l1tail = L1;
while (prev1->next != NULL && prev2->next != NULL) {
if (prev1->next->data == prev2->next->data) {
l1tail->next = prev1->next;
l1tail = prev1->next;
prev1 = prev1->next;
prev2 = prev2->next;
}
else if (prev1->next->data < prev2->next->data) prev1 = prev1->next;
else prev2 = prev2->next;
}
l1tail->next = NULL;
return L1;
}
/*16.两个链表分别是一个整数序列,判断B是否是A的子序列
1. 不断比较两个先驱指针的next
2. 若相等,同时后移
3. 若不等,有两种可能,
1. 如果该节点是一个子序列的开始,则比较其后续节点与son的后续节点
2. 否则,比较其后续结点和son的开始节点
*/
bool if_sonlist(LinkList parent, LinkList son) {
LinkList sonhead = son;
while (parent->next != NULL) {
if (son->next == NULL) return true;
if (parent->next->data == son->next->data) {
parent = parent->next;
son = son->next;
}
else if (parent->next->data == sonhead->next->data) {
parent = parent->next;
son = sonhead->next;
}
else {
parent = parent->next;
son = sonhead;
}
}
return false;
}
//17. 判断带头结点的循环双链表是否对称
bool if_symmetry(DLinkList L) {
DLinkList lft = L->next, rht = L->prior;
while (lft != rht && lft != rht->next) {//边界有两种情况,偶数时,lft会跑到rht右边,奇数时,两者碰到一起
if (lft->data == rht->data) {
lft = lft->next;
rht = rht->prior;
}
else return false;
}
return true;
}
//18.两个循环单链表,将链表h2链接到链表hl之后,要求链接后的链表仍保持循环链表形式
LinkList merge_loop_list(LinkList L1, LinkList L2) {
LinkList l1tail = L1, l2tail = L2;
while (l1tail->next != L1) l1tail = l1tail->next;
while (l2tail->next != L2) l2tail = l2tail->next;
l1tail->next = L2->next;
l2tail->next = L1;
return L1;
}
//19.反复找出循环单链表中结点值最小的结点并输出,然后将该结点从中删除,直到单链表空为止,再删除表头结点
void find_and_del_minnode_loop(LinkList L) {
LinkList node = L->next;
if (node == L) return;
LinkList min_node_prev = L, work_node = node;
while (work_node->next != L) {
if (work_node->next->data < min_node_prev->next->data) min_node_prev = work_node;
work_node = work_node->next;
}
cout << "del min_node:" << min_node_prev->next->data << endl;
LinkList temp = min_node_prev->next;
min_node_prev->next = min_node_prev->next->next;
delete temp;
find_and_del_minnode_loop(L);
}
//20.判断单链表是否有环
bool if_has_cycle(LinkList L) {
LinkList slow = L, fast = L;
while (1) {
slow = slow->next;
fast = fast->next->next;
if (slow == fast) return true;
if (fast == NULL || fast->next == NULL) return false;
}
return false;
}
LNode* FindLoopStart(LNode* head) {
LNode* fast = head, * slow = head;
while (fast != NULL && fast->next != NULL) {
slow = slow->next; //每次走一步
fast = fast->next->next; //每次走两步
if (slow == fast) break; //相遇
}
if (fast == NULL || fast->next == NULL)
return NULL; //没有环,返回NULL
LNode* pl = head, * p2 = slow;
while (pl != p2) {
//分别指向开始点、相遇点
pl = pl->next;
p2 = p2->next;
}
return pl; //返回入口点
}
//真题1.查找带头结点的链表中倒数第k个位置上的结点
int find_k_rev_node(LinkList L, int k) {
LinkList prev = L, after = L;
for (int i = 0;i < k;i++) {
if (after == NULL) return 0;
after = after->next;
}
while (after != NULL) {
after = after->next;
prev = prev->next;
}
cout << "the node is:" << prev->data << endl;
return 1;
}
//真题2.strl和str2分别指向两个单词所在单链表的头结点,找出由strl和str2所指向两个链表共同后缀的起始位置
LinkList find_public_charnode(LinkList L1, LinkList L2) {
if (L1->next == NULL || L2->next == NULL) return NULL;
int len1 = len_of_list(L1->next), len2 = len_of_list(L2->next);
LinkList longer = (len1 > len2) ? L1->next : L2->next;
LinkList shorter = (len1 > len2) ? L2->next : L1->next;
for (int i = 0;i < abs(len1 - len2);i++) longer = longer->next;
while (longer != NULL) {
if (longer == shorter) return longer;
longer = longer->next;
shorter = shorter->next;
}
return longer;
}
//真题3.用单链表保存m个整数,其绝对值均小于n,对于链表中data的绝对值相等的结点,仅保留第一次出现的结点而删除其余绝对值相等的结点
LinkList remove_sameabs(LinkList& L, int n) {
bool bucket[n];
for (int i = 0;i < n;i++) bucket[i] = 0;
LinkList prev = L;
while (prev->next != NULL) {
if (bucket[abs(prev->next->data)] == true) {
LinkList temp = prev->next;
prev->next = prev->next->next;
delete temp;
}
else {
bucket[abs(prev->next->data)] = true;
prev = prev->next;
}
}
print_linklist(L);
return L;
}
//真题4.线性表L =(a1,a2,,an)采用带头结点的单链表保存,就地将其排序为(a1,an,a2,an-1,,,)
LinkList resort_list(LinkList L) {
LinkList p = L, q = L, r;
while (q != NULL && q->next != NULL) {//寻找中点
q = q->next->next;
p = p->next;
}
q = p->next;//令q为后半段第一个节点
p->next = NULL;//断开前半段
while (q != NULL) {//逆置后半段
r = q->next;
q->next = p->next;
p->next = q;
q = r;
}
LinkList prev;
prev = L->next;//前半段第一个节点
q = p->next;//后半段第一个节点
while (q != NULL) {//也可以是prev!=p
r = q->next;//暂存的r是后半段链表下一个要处理的节点
q->next = prev->next;
prev->next = q;//将n-i+1号节点插入到i号节点后
prev = q->next;
q = r;
}
p->next = NULL;//最后形成的链表到p为止
return L;
}
int main() {
int temp[8] = { 2, 12, 23, 33,54, 72, 83, 99 };
int temp2[3] = { 3,17, 23 };
LinkList nodes = new LNode;
LinkList nodes2 = new LNode;
build_nodelist(nodes, temp,
sizeof(temp) / sizeof(temp[0])); // 生成带头结点的测试链表
build_nodelist(nodes2, temp2,
sizeof(temp2) / sizeof(temp2[0])); // 生成带头结点的测试链表
/* DLinkList doublelist = new DoubleLNode;
build_loop_double_list(doublelist, temp, sizeof(temp) / sizeof(temp[0])); */
//nodes2 = merge_list(nodes2, nodes);
// del_by_val(nodes->next,22);//传入头结点的next就可以视为无头结点链表
// del_by_val_withhead(nodes,22);
// print_linklist_rev(remove_head(nodes));
// del_min_withhead(nodes);
//nodes = rev_insite_withhead(nodes);
//insertsort_list(nodes);
//del_val_inrange(nodes,10,30);
//find_public_node(nodes,nodes2);
//print_and_del_sorted_list(nodes2);
/* auto listpair = tear_list(nodes);
print_linklist(listpair.first);
print_linklist(listpair.second); */
/* auto nodespair = tear_list_rev(nodes);
print_linklist(nodespair.first);
print_linklist(nodespair.second); */
//remove_samepart_list(nodes);
//nodes = merge_and_sort(nodes2, nodes);
//print_linklist(build_list_from_public(nodes,nodes2));
//print_linklist(list_intersection(nodes,nodes2));
//cout << "A is B's parent?" << if_sonlist(nodes, nodes2) << endl;
//cout << "symmetry? " << if_symmetry(doublelist) << endl;
//print_loop_linklist(merge_loop_list(build_loop_list(nodes, temp, sizeof(temp) / sizeof(temp[0])), build_loop_list(nodes2, temp2, sizeof(temp2) / sizeof(temp2[0]))));
//find_and_del_minnode_loop(build_loop_list(nodes, temp, sizeof(temp) / sizeof(temp[0])));
//cout << "has a cycle?" << if_has_cycle(nodes) << endl;
//find_k_rev_node(nodes, 8);
//find_public_charnode(nodes, nodes2);
//remove_sameabs(nodes, 200);
print_linklist(resort_list(nodes));
//print_linklist(doublelist);
//print_linklist(nodes);
}
栈&&队列&&矩阵
栈
c++表示:
1 |
|
注意进出栈对应修改data和top的顺序相反
链栈的优点是便于多个栈共享存储空间和提高其效率,且不存在栈满上溢的情况。通常采用单链表实现,并规定所有操作都是在单链表的表头进行的。
实现中规定链栈没有头结点,Lhead指向栈顶元素
两个顺序栈可共享一个连续数组框架,增长方向相对,一个栈底是0,一个是MaxSize-1,只当top1-top0==1时栈满
将中缀表达式转换为后缀表达式的算法思想如下:
从左向右开始扫描中缀表达式;
遇到数字时,加入后缀表达式;
遇到运算符时:
a. 若为(,入栈;
b. 若为),则依次把栈中的运算符加入后缀表达式,直到出现(,从栈中删除(;
c. 若为除括号外的其他运算符,当其优先级高于除(外的栈顶运算符时,直接入栈。否则从栈顶开始,依次弹出比当前处理的运算符优先级高和优先级相等的运算符,直到一个比它优先级低的或遇到了一个左括号为止。
当扫描的中缀表达式结束时,栈中的所有运算符依次出栈加入后缀表达式。
队列
先进先出的数据结构,但其顺序实现会产生难以判满的问题,即rear==MaxSize时,可能前有空槽
循环队列:
- 初始时:
Q.front=Q.rear=0 - 队首指针进1:
Q.front= (Q.front+1)%MaxSize - 队尾指针进1:
Q.rear=(Q.rear+1)%MaxSize - 队列长度:
(Q.rear+MaxSize-Q.front)%MaxSize
可以约定以队头指针在队尾指针的下一位置作为队满的标志,即减少一个存储单元,此时:
- 队满条件:
(Q.rear+1)%MaxSize==Q.front - 队空条件:
Q.front==Q.rear
或者增设size成员,tag成员,tag等于0时,若因删除导致Q.front==Q.rear,则为队空;tag等于1时,若因插入导致Q.front==Q.rear,则为队满
增设一个tag的整型变量,进队时置tag为1,出队时置tag为0,以tag判断满空
1 |
|
链式队列:
需要队头和队尾指针,front指向第一个节点,rear指向最后一个节点
队空条件:front==rear==NULL
也可以设置一个头结点,统一插入和删除操作
1 |
|
双端队列:
允许两端都可以进行入队和出队操作的队列
- 输出受限的双端队列:允许在一端进行插入和删除,但在另一端只允许插入
- 输入受限的双端队列:允许在一端进行插入和删除,但在另一端只允许删除
栈被应用于:递归,前后缀运算符,括号匹配
而队列应用于:按广度遍历,操作系统的任务调度
数组与矩阵
一维数组可视为一个线性表;二维数组可视为其元素也是定长线性表的线性表,数组是定长的,在逻辑上有自己的维数和长度(但c与c++不检查是否越界)
一维数组:\({\mathsf{L O C}}(a_{i})={\mathsf{L O C}}(a_{0})+i\times L\ \ (0\leq i<n)\)
二维数组(h1,h2分别是行列的最大值) 按行存储时:
\[{\mathrm{LOC}}(a_{i,j})={\mathrm{LOC}}(a_{0,0})+\left[i\times(h_{2}+1)+j\right]\times L\]
按列存储时:
\[\mathrm{LOC}(a_{i,j})=\mathrm{LOC}(a_{0,0})+\bigl[j\times(h_{1}+1)+i\bigr]\times L\]
二维数组一般从0开始索引,矩阵一般从1开始
矩阵可以用一些方法压缩
- 对称矩阵 ,元素下标之间的对应关系:\(k=\frac{i(i-1)}{2}+j-1,\qquad i\geqslant j(i<j时两者互换)\)
- 下三角矩阵(上三角区元素都是常量)
\[k= \begin{cases} \frac{i(i-1)}{2}+j-1,\qquad i\geq j \\ \frac{n(n+1)}{2},\qquad\qquad\qquad i<j \\ \end{cases}\]
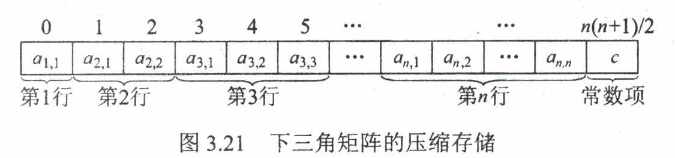
按列存储且数组从1开始索引时: \(k=(j-1)(2n-j+2)/2+i-j+1\)
- 上三角矩阵,与下三角相反 \[k= \begin{cases} \frac{(i-1)(2n-i+2)}{2}+(j-i)\qquad i\le{j}\\ \frac{n(n+1)}{2},\qquad\qquad\qquad\qquad i>j \\ \end{cases}\]

按列存储且数组从1开始索引时: \(k=j(j-1)/2+i\)
- 三对角矩阵,对任意\(|i-1|> 1\)有\(a_{i,j}=0\)
\(i = \left\lfloor(k+1)/3+1\right\rfloor \qquad j = k-2i+3\)

- 稀疏矩阵:非零元素远少于零元素的矩阵,用三元组(i,j,value)储存

也可以用十字链表(行单链表和列单链表)存储
树
- 树是递归定义的
- 一个结点的孩子个数称为该结点的度,树中结点的最大度数称为树的度
- 度大于0的结点称为分支结点(又称非终端结点);度为0 (没有子女结点)的结点称为叶结点(又称终端结点)
- 结点的层次从树根开始定义,根结点为第1层,它的子结点为第2层,以此类推。双亲在同一层的结点互为堂兄弟
- 结点的深度是从根结点开始自顶向下逐层累加的。
- 结点的高度是从叶结点开始自底向上逐层累加的。
- 树的高度(或深度)是树中结点的最大层数
- 路径长度是路径上所经过的边的个数
- 森林是树的集合
基本性质:
- 树中的结点数等于所有结点的度数之和加1(根节点)
n0+n1+...+nk = n1+2*n2+...+k*nk+1 - 度m的数第i层至多有 \(m^{i-1} 且 i\ge1\)
- 高度h的m叉树最多有 \((m^{h}-1)/(m-1)\)个结点
- n个结点的m叉树最小高度为 \(\lceil\log_{m}(n(m-1)+1)\rceil\)
二叉树
每个结点至多只有两棵子树的树,子树分左右,即使只有一个节点
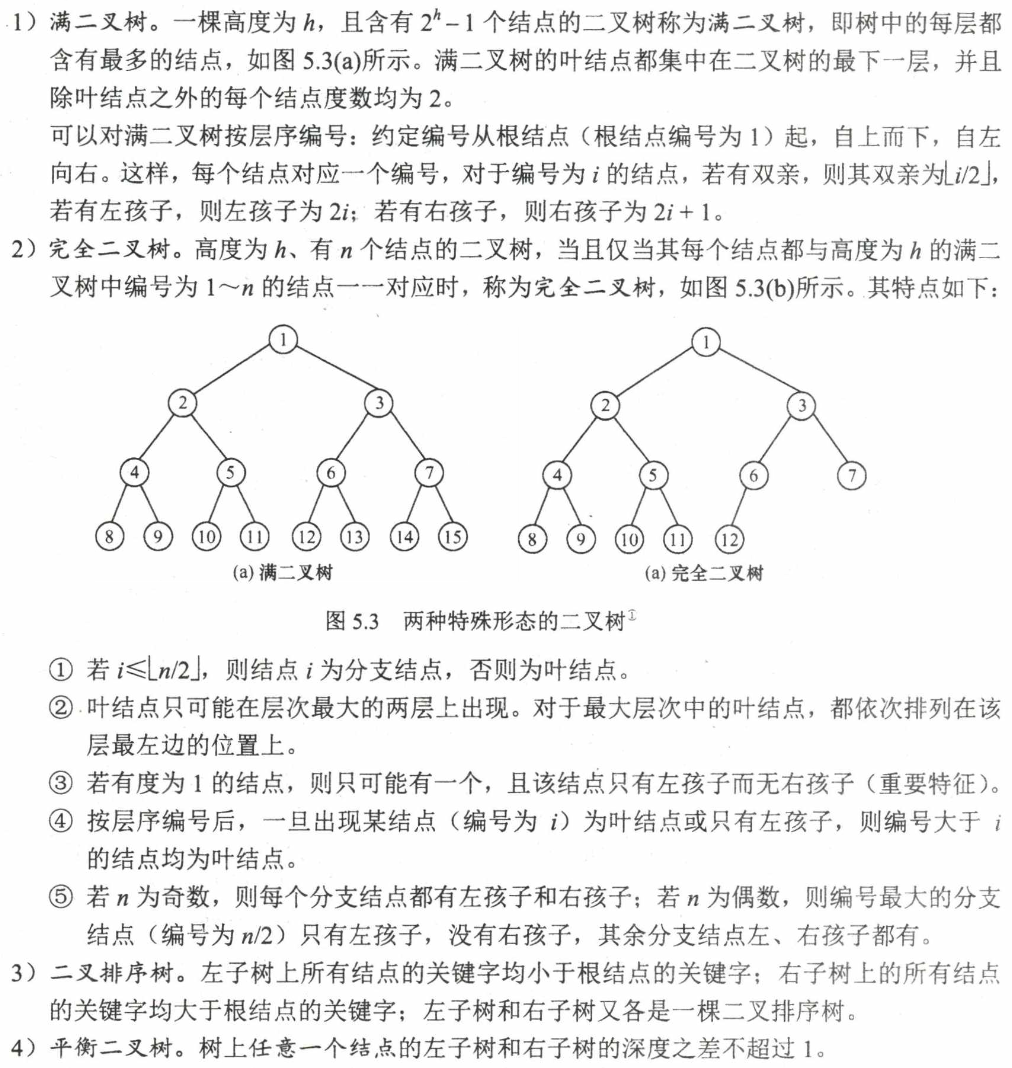
基本性质:
- ni表示度i的节点数,则
n0 = n2 + 1 - 非空二叉树第k层最多有 \(2^{k-1}\) 个结点
- 高度h的二叉树至多有\(2^h-1个结点\)
- 对完全二叉树编号:
- 当i>1时,结点i的双亲的编号为 \(\lfloor i/2 \rfloor\) ,即当i为偶数时,其双亲的编号为i/2,它是双亲的左孩子;当i为奇数时,其双亲的编号为(i-1)/2,它是双亲的右孩子
- 当 \(2i \le n\) 时,结点i的左孩子编号为2i,否则无左孩子
- 当 \(2i+1 \le n\) 时,结点i的右孩子编号为2i+1,否则无右孩子
- 结点i所在层次(深度)为 \(\lfloor\log_{2}i\rfloor+1\)
- 具有n个(n>0)结点的完全二叉树的高度为 \(\lceil\log_{2}(n+1)\rceil\ 或 \lfloor\log_{2}n\rfloor+1\)
\[2^{h^{-1}}-1\lt n\leqslant2^{h}-1\]
存储结构:
- 顺序存储,一般从1开始索引,a[i]结点的左右子节点分别是a[2i],a[2i+1],父节点(如果存在)是ai/2
- 链式存储,n个结点产生2n个链域,其中n-1个结点占据一个链域(除了根节点),因此含有n个结点的二叉链表中,含有n + 1个空链域
中序加任何一种其他顺序可以确定一颗二叉树,而只知道先后序列不行
基本操作的cpp实现:
1 | { |
线索二叉树
n个结点的链式数有n+1个空链接,利用这些指针来存储前驱和后继节点
规定若无左子树,令lchild指向其前驱结点;若无右子树,令rchild指向其后继结点,并用两个tag标记前后驱节点是否启用
tag==0时,表示节点是孩子节点,否则是前后节点
线索二叉树的先驱后继是相对于一种遍历顺序的,例如先序线索时如图: 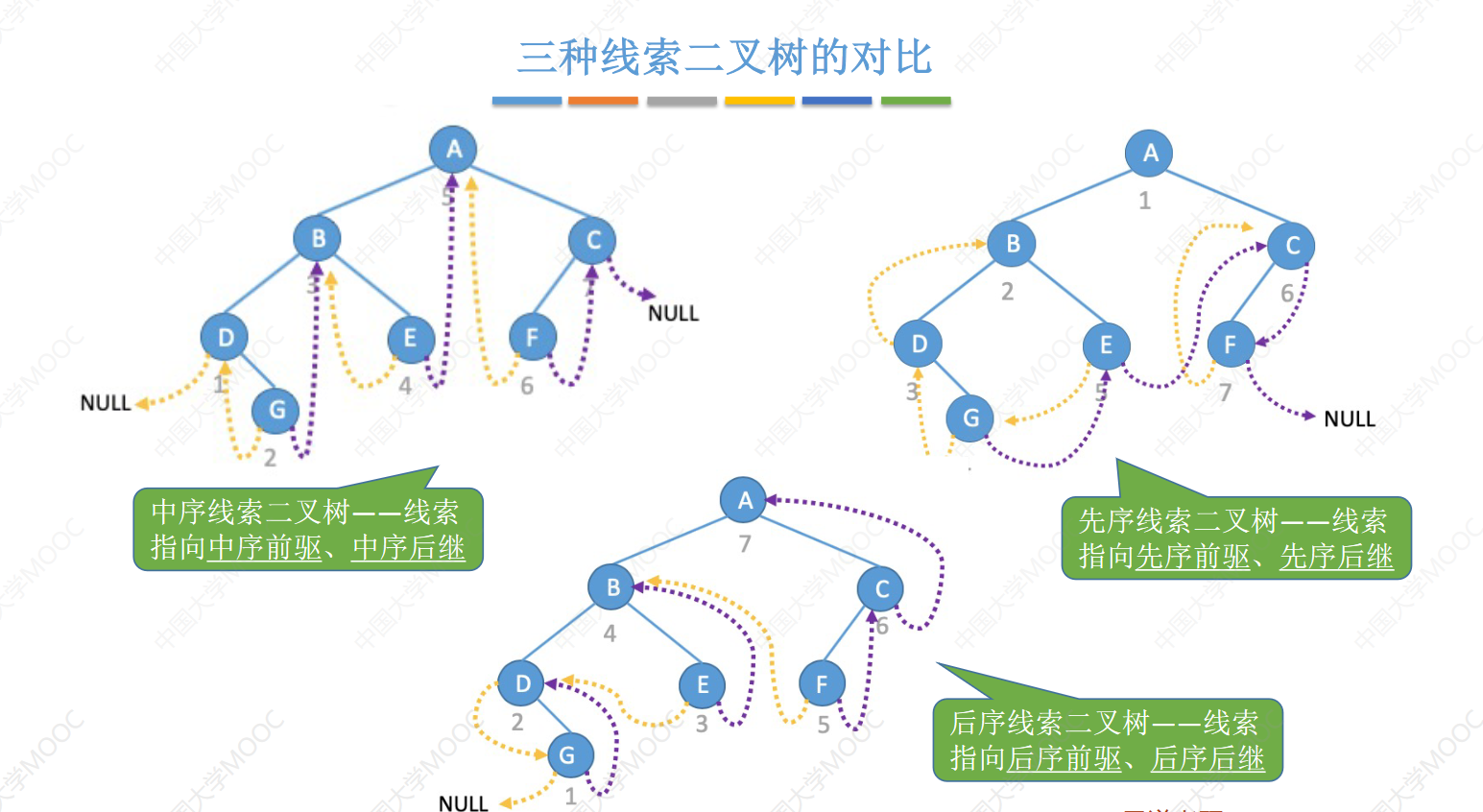 先序线索二叉树无法确定前驱节点,后序线索二叉树无法确定后继节点
先序线索二叉树无法确定前驱节点,后序线索二叉树无法确定后继节点
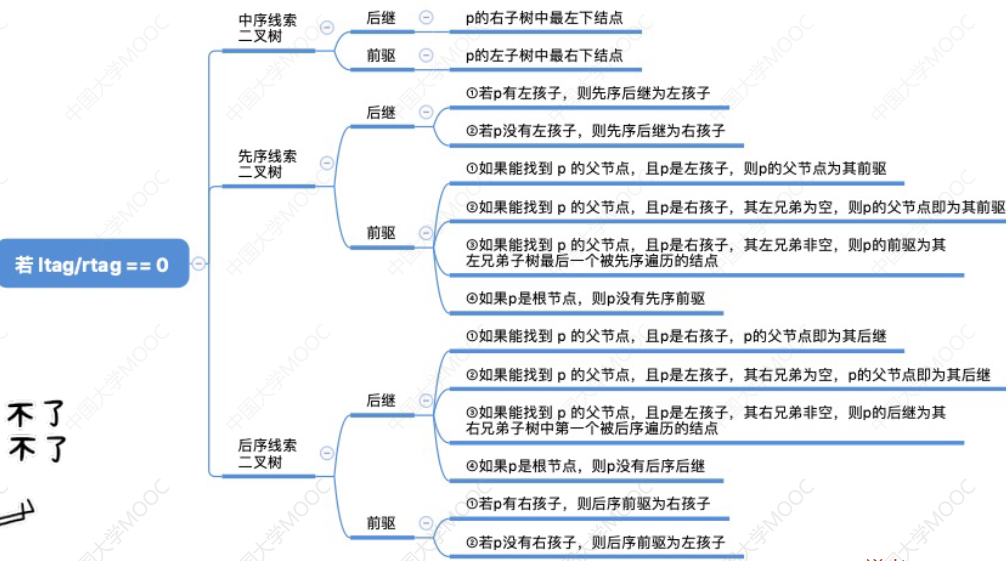
1 | //线索二叉树 |
- 后向遍历可以输出子节点到祖先结点的路径
森林
可以表示任何树的方法:
双亲表示法:采用一组连续空间来存储每个结点,同时在每个结点中增设一个伪指针,指示其双亲结点在数组中的位置,求结点的孩子时则需要遍历整个结构
1
2
3
4
5
6
7
8
9
10//树的双亲节点表示法
struct PTNode {
ElemType data;
int parent;
};
struct PTree {
PTNode nodes[MaxSize];
int n;
};孩子表示法,将每个结点的孩子结点都用单链表链接起来,每个结点都有自己的孩子链表(可以为空),寻找双亲的操作需要遍历
孩子兄弟表示法,以二叉链表作为树的存储结构,即二叉树的左指针是孩子链表,右指针是兄弟链表,从当前结点查找其双亲结点比较麻烦,也是树和二叉树相互转化的方法
1 | struct CSNode { |
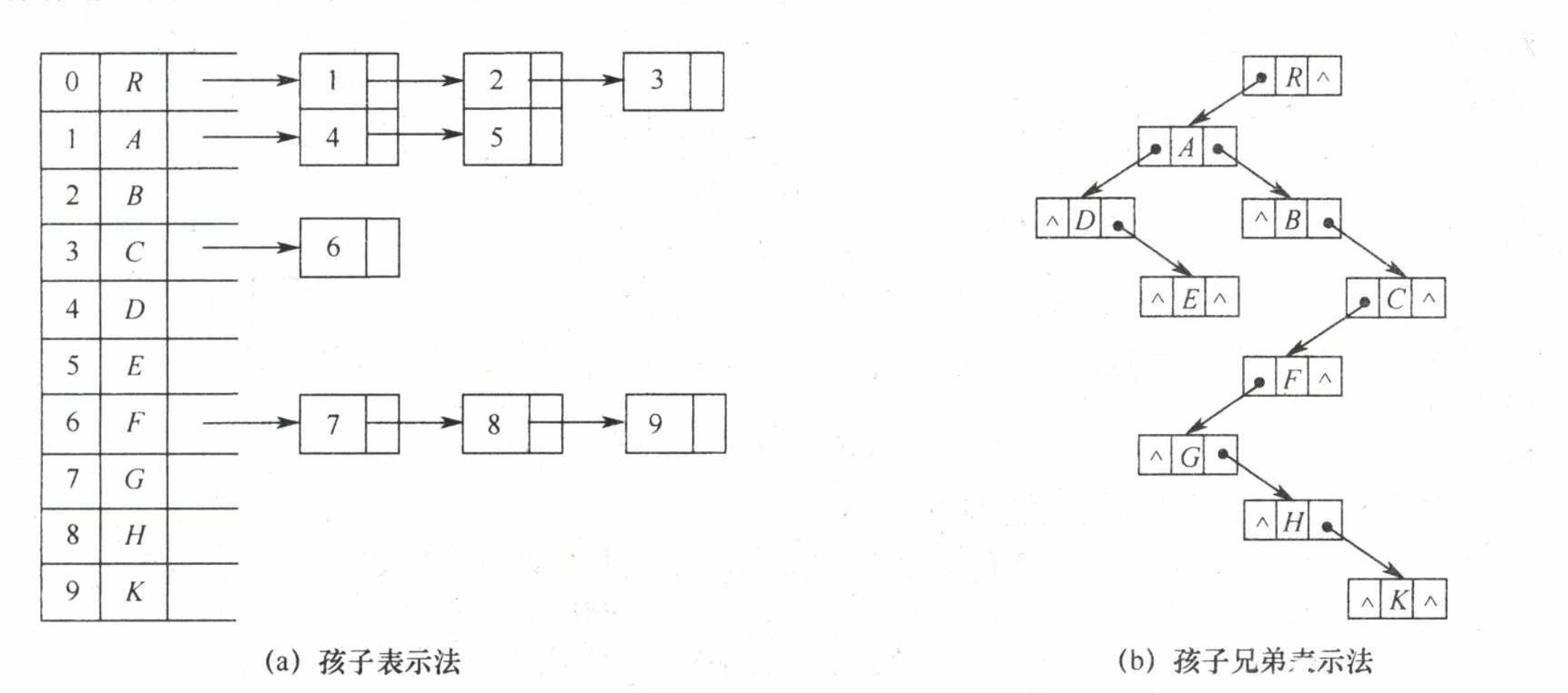 任意一棵和树对应的二叉树的右子树必空
任意一棵和树对应的二叉树的右子树必空 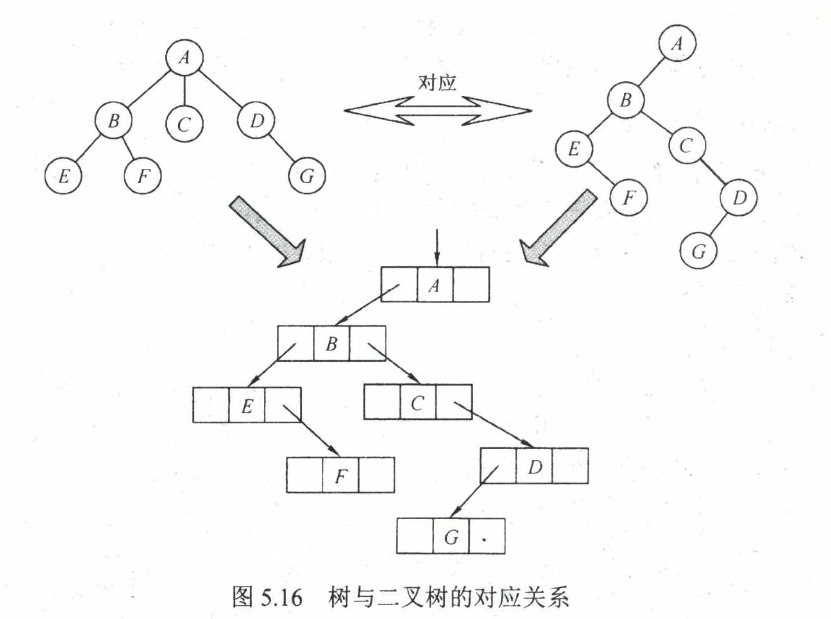
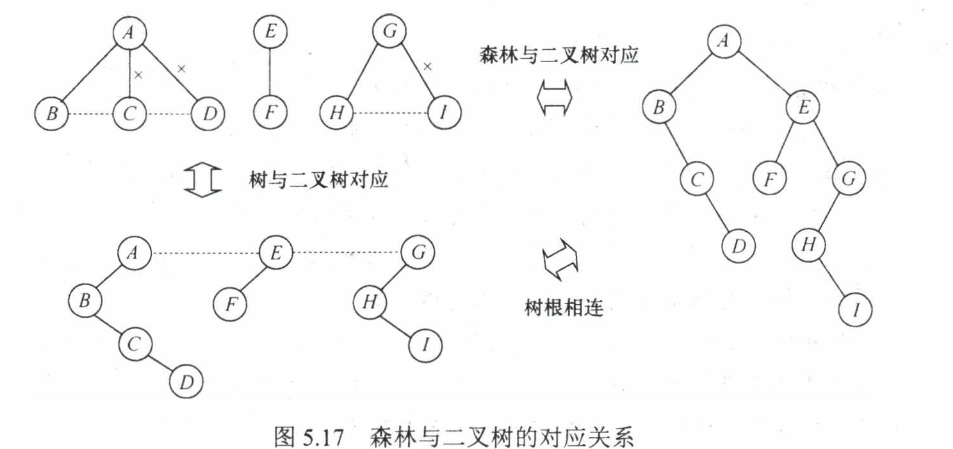
森林和二叉树的转化类似树和二叉树,每一棵树转化成二叉树,视为第一个树的兄弟,被连接至根节点的右侧
- 树的遍历分为先根和后根,因为转化成二叉树时根节点只有左子树,所以不需要区分左右
- 森林的遍历则有先序和中序
- 先序指先访问第一棵树的根节点,然后递归访问其子节点与其他树
- 中序指先递归访问第一棵树的子节点,然后访问其根节点,最后递归访问其他树
森林的中序也可以理解成后序,因为对每棵树来说,根节点被最后访问
- 转换为二叉树时,树的每个分支结点的所有子结点中的最右子结点无右孩子,根结点转换后也没有右孩子,因此,对应二叉树中无右孩子的结点个数=分支结点数+1
树的应用
从树的根到任意结点的路径长度(经过的边数)与该结点上权值的乘积,称为该结点的带权路径长度
含有n个带权叶结点的二叉树中,其中带权路径长度(WPL)最小的二叉树称为哈夫曼树,也称最优二叉树
将一段文本的字符频率作为权值的哈夫曼树,则可以用来进行哈夫曼编码,实现文本的压缩传输,这也是cs106b的期末作业,代码如下
1 | //作业其实都用的斯坦福自己的数据结构库,相比stl操作更简单 |
并查集
简单地说并查集就是用数组树来表示的集合,其基本操作如下 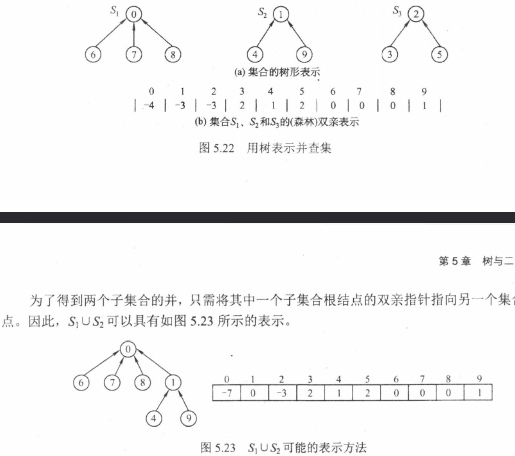
1 | int UFSets[MaxSize]; //集合元素数组(双亲指针数组) |
- 可用于实现克鲁斯卡尔算法(判断是否加入一条边之前,先查找这条边关联的两个顶点是否属于同一个集合)
- 可用于判断无向图的连通性,即整个图遍历后,连通分量一一对应集合
- 可用二叉树检查编码是否满足前缀不重复特性,即只有编码树的叶节点能对应被编码的一个字符
练习题汇总: 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285//0.找到顺序存储二叉树的公共父节点
int find_public_parent(Arraytree T, int i, int j) {
if (i < 1 || j < 1) return -1;
while (i != j) {
if (i > j) i = parent(i);
else j = parent(j);
}
if (i == j && i > 0) return T.data[i];
return -1;
}
//1.二叉树的自下而上、从右到左的层次遍历算法
void rev_levelOrder(LinkTree T) {//相当于层次遍历的相反顺序,即用栈来存储队列遍历产生的结果
stack<TreeNode*> stack;
queue<LinkTree> qe;
qe.push(T);
while (!qe.empty()) {
TreeNode* node = qe.front();
qe.pop();
stack.push(node);
if (node->left != nullptr)
qe.push(node->left); // 左子节点入队
if (node->right != nullptr)
qe.push(node->right); // 右子节点入队
}
while (!stack.empty()) {
visit(stack.top());
stack.pop();
}
}
//2.递归求二叉树高度
int height(LinkTree T) {
if (T == nullptr) return 0;
return max(height(T->left), height(T->right)) + 1;//优雅的两行实现,但不是尾递归?
}
//3.非递归算法求二叉树的高度
int height2(LinkTree T) {//层序遍历中存储每层最右侧指针,每次出队元素和最右侧指针相同时,高度++
if (T == nullptr) return 0;
int height = 0;
TreeNode* last = T;
queue<LinkTree> qe;
qe.push(T);
while (!qe.empty()) {
LinkTree node = qe.front();
qe.pop();
if (node->left != nullptr) qe.push(node->left);
if (node->right != nullptr) qe.push(node->right);
if (node == last) {
height++;
last = qe.back();
}
}
return height;
}
//4.先序遍历序列和中序遍历序列分别存于两个一维数组,构建二叉树
LinkTree build_tree_from_pre_and_in(int pre[], int in[], int pre1, int pre2, int in1, int in2) {
//pre1,pre2分别是先序的第一和最后一个节点下标
LinkTree root = new TreeNode;
root->data = pre[pre1];
int i;
for (i = in1;in[i] != root->data;i++);//找到根节点来划分左右子树
int left_len = i - in1;
int right_len = in2 - i;
if (left_len != 0) root->left = build_tree_from_pre_and_in(pre, in, pre1 + 1, pre1 + left_len, in1, in1 + left_len - 1);
else root->left = nullptr;
if (right_len != 0) root->right = build_tree_from_pre_and_in(pre, in, pre2 - right_len + 1, pre2, in2 - right_len + 1, in2);
else root->right = nullptr;
return root;
}
//5.判别给定二叉树是否是完全二叉树
bool if_complete(LinkTree T) {
queue<LinkTree> qe;
qe.push(T);
while (!qe.empty()) {
LinkTree node = qe.front();
qe.pop();
if (node) {
qe.push(node->left);
qe.push(node->right);
}
else {
while (!qe.empty()) {
if (qe.front()) return false;
qe.pop();
}
}
}
return true;
}
//6.求给定二叉树的所有双分支结点个数
int num_of_twinnode(LinkTree& T) {//优雅的递归
if (T == nullptr) return 0;
if (T->left && T->right) return 1 + num_of_twinnode(T->left) + num_of_twinnode(T->right);
else return num_of_twinnode(T->left) + num_of_twinnode(T->right);
}
//7.交换所有结点的左右子树
void swap_lr(LinkTree& T) {
if (T) {
swap_lr(T->left);
swap_lr(T->right);
LinkTree L = T->left;
T->left = T->right;
T->right = L;
}
}
//8.求先序遍历序列中第k个节点的值
int preOrder_kth_node(LinkTree T, int& i, int& k) {
if (k <= 0) return INT32_MIN;//输入不合理,直接退出
if (k == i) return T->data;//由于每次递归i只+1,因此达到k时必然立刻返回
int val;
if (T->left) val = preOrder_kth_node(T->left, ++i, k);//存储对左子树遍历后的值
if (i == k) return val;//如果遍历完左子树,且i==k,那么返回值必然是ith节点的data
else if (T->right) return preOrder_kth_node(T->right, ++i, k);//如果右孩子不空,才可以++i
else return INT16_MIN;
}
//9.对于树中每个元素值为x的结点,删除以x为根的子树,并释放相应的空间
void del_val_x_node_helper(LinkTree& T, int& x, LinkTree& pre, bool is_lft) {
if (!T) return;
del_val_x_node_helper(T->left, x, T, 1);
del_val_x_node_helper(T->right, x, T, 0);
if (T->data == x) {
del_node(T);//递归删除T的所有子节点
if (is_lft) pre->left = nullptr;
else pre->right = nullptr;
}
}
void del_val_x_node(LinkTree& T, int x) {
if (T->data == x) del_node(T);
else {
del_val_x_node_helper(T->left, x, T, 1);
del_val_x_node_helper(T->right, x, T, 0);
}
}
//10.打印值为x的结点的所有祖先,假设值为x的结点不多于一个
bool print_ancestor_helper(LinkTree& T, int& x);
void print_ancestor_of_xval(LinkTree& T, int x) {
print_ancestor_helper(T, x);
}
bool print_ancestor_helper(LinkTree& T, int& x) {
//递归返回true表示该节点的子节点中有x节点,因此可以打印,否则不能打印
if (!T) return false;
if (T->data == x) return true;
bool val1 = print_ancestor_helper(T->left, x);
if (val1 == 1) cout << T->data << '\n';
bool val2 = print_ancestor_helper(T->right, x);
if (val2 == 1) cout << T->data << '\n';
return val1 || val2;
}
//非递归实现用到栈,访问到值为x的结点时,栈中所有元素均为该结点的祖先,依次出栈打印
//11.p和q分别为指向该二叉树中任意两个结点的指针,寻找其最近公共祖先
//祖先有两种可能:1.该节点左右子树各自存在pq 2.节点本身是p或q且其左子树或右子树有另一个孩子节点
bool ancestor_helper(LinkTree tree, LinkTree& p, LinkTree& q, LinkTree& res) {
if (!tree) return false;
bool is_lft_son = ancestor_helper(tree->left, p, q, res);
bool is_rht_son = ancestor_helper(tree->right, p, q, res);
if ((is_lft_son && is_rht_son) || ((tree->data == p->data || tree->data == q->data) && (is_lft_son || is_rht_son))) {
res = tree;
}
return is_lft_son || is_rht_son || (tree->data == p->data || tree->data == q->data);
}
LinkTree find_ancestor_root(LinkTree root, LinkTree p, LinkTree q) {
LinkTree res = nullptr;
ancestor_helper(root, p, q, res);
return res;
}
//12.求非空二叉树的宽度(结点数最多的一层的结点个数)
int width_of_tree(LinkTree& T) {
if (!T) return 0;
int max_layer = 1;
queue<LinkTree> qe;
queue<LinkTree> next_qe;
qe.push(T);
while (true) {
while (!qe.empty()) {
LinkTree t = qe.front();
qe.pop();
if (t->left) next_qe.push(t->left);
if (t->right) next_qe.push(t->right);
}
if (next_qe.empty()) break;
max_layer = max(int(next_qe.size()), max_layer);
qe = next_qe;
while (!next_qe.empty()) next_qe.pop();
}
return max_layer;
}
//13.一棵满二叉树(所有结点值均不同),已知其先序序列为pre,求其后序序列post。
void find_post_from_pre(int pre[], int l1, int h1, int post[], int l2, int h2) {
int half;
if (h1 >= l1) {
post[h2] = pre[11];
half = (h1 - l1) / 2;
find_post_from_pre(pre, 11 + 1, 11 + half, post, 12, 12 + half - 1); //转换左子树
find_post_from_pre(pre, 11 + half + 1, h1, post, 12 + half, h2 - 1); //转换右子树
}
}
//14.将二叉树的叶结点按从左到右的顺序连成一个带头结点单链表,表头指针为head,叶结点的右指针域来存放单链表指针
void tree_to_link_helper(LinkTree t, LinkTree& tail) {
if (!t->left && !t->right) {
tail->right = t;
tail = t;
}
else {
tree_to_link_helper(t->left, tail);
tree_to_link_helper(t->right, tail);
}
}
LinkTree tree_to_link(LinkTree& T) {
LinkTree head = new TreeNode;
LinkTree tail = head;
head->data = INT16_MIN;
head->left = nullptr;
head->right = tail;
tree_to_link_helper(T, tail);
return head;
}
/*15.判断二叉树是否相似,相似的定义:
T1和T2都是空的二叉树或都只有一个根结点;
或者T1的左子树和T2的左子树相似,且T1的右子树和T2的右子树相似
*/
bool if_tree_similar(LinkTree& T1, LinkTree& T2) {
if (!T1 && !T2) return true;
if (!T1 || !T2) return false;
return if_tree_similar(T1->left, T2->left) && if_tree_similar(T1->right, T2->right);
}
//真题1.求出二叉树中所有叶结点的带权路径长度之和,需要权值乘层高
//视data为weight
void sum_weight_helper(LinkTree t, int& sum, int path_weight, int depth) {
if (!t) return;
if (!t->left && !t->right) {
sum += path_weight + t->data * depth;
}
path_weight += t->data * depth;
sum_weight_helper(t->left, sum, path_weight, depth + 1);
sum_weight_helper(t->right, sum, path_weight, depth + 1);
}
int sum_weight(LinkTree& t) {
int w = 0;
sum_weight_helper(t, w, 0, 0);
return w;
}
//16.在中序线索二叉树里查找指定结点在后序的前驱结点
ThreadTree find_pre_node(ThreadTree& t, ThreadTree& p) {
//在中序线索二叉树t中,求指定结点p在后序下的前驱结点q
ThreadTree q;
if (p->rtag == 0) //若p有右子女,则右子女是其后序前驱
q = p->rchild;
else if (p->ltag == 0) //若p只有左子女,则左子女是其后序前驱
q = p->lchild;
else if (p->lchild == NULL)
q = NULL; //p是中序序列第一结点,无后序前驱
else { //顺左线索向上找p的祖先,若存在,再找祖先的左子女
while (p->ltag == 1 && p->lchild != NULL)
p = p->lchild;
if (p->ltag == 0)
q = p->lchild; //p结点的祖先的左子女是其后序前驱
else
q = NULL; //仅有单支树(p是叶子),己到根结点,p无后序前驱
}
return q;
}
图
图G由顶点集V和边集E组成,即G=(V,E)
其中,E的组成是(u,v)
可分为有向和无向图
- 有向图的边用<1,2>表示
- 无向图的边用(1,2)表示
- 不存在重复边,没有连接自己的边的图是简单图
- 某两个顶点之间的边数大于1条,又允许顶点通过一条边和自身关联,则称图G为多重图
- 对无向图,任意两个结点都有边连接的无向图称为完全图,即n(n-1)/2条边,有向完全图的边数则是完全图边数的翻倍
- V和E的子集构成的图(必须能构成图),是原图的子图,若两者的V相等,则称为生成子图
- 极大连通子图是无向图的连通分量、极大即要求该连通子图包含其所有的边;极小连通子图是既要保持图连通又要使得边数最少的子图。
- 无向图中,任意两个节点连通(存在路径)的图是连通图,无向图中的极大连通子图称为连通分量
- 在有向图中,如果有一对顶点V和W,从V到W和从W到V间都有路径,则称这两个顶点是强连通的。若图中任何一对顶点都是强连通的,则称此图为强连通图。有向图中的极大强连通子图称为有向图的强连通分量
- 连通图的生成树是包含图中全部顶点的一个极小连通子图(n-1条边),减少一条边则不连通,增加一条边则形成环
- 无向图中顶点v的度是指依附于顶点v的边的条数,即TD(v),无向图的全部顶点的度的和等于边数的2倍
- 有向图的全部顶点的入度之和与出度之和相等,并且等于边数
- 边有权的图称为带权图(网)
- 稀疏和稠密是相对概念,一般VlogV是分界点
- 若一个图有n个顶点,并且有大于n-1条边,则此图一定有环
- 顶点不重复出现的路径称为简单路径,除第一个顶点和最后一个顶点外,其余顶点不重复出现的回路称为简单回路
- 两个结点间最短路径的长度是两者的距离,不连通时为无穷
- 一个顶点的入度为0、其余顶点的入度均为1的有向图,称为有向树
存储
邻接矩阵法
一个一维数组存储图中顶点的信息,用一个二维数组存储图中边的信息
A[i][j]可以表示边是否存在(1/0),也可以表示权值(此时0/无穷表示不存在)
1
2
3
4
5
6
7using VertexType = char;
using EdgeType = int;
struct Matrix_Graph {
VertexType Vex[MaxVertexNum];
EdgeType Edge[MaxVertexNum][MaxVertexNum]; //邻接矩阵,边表
int vexnum, arcnum; //图的当前顶点数和弧数
};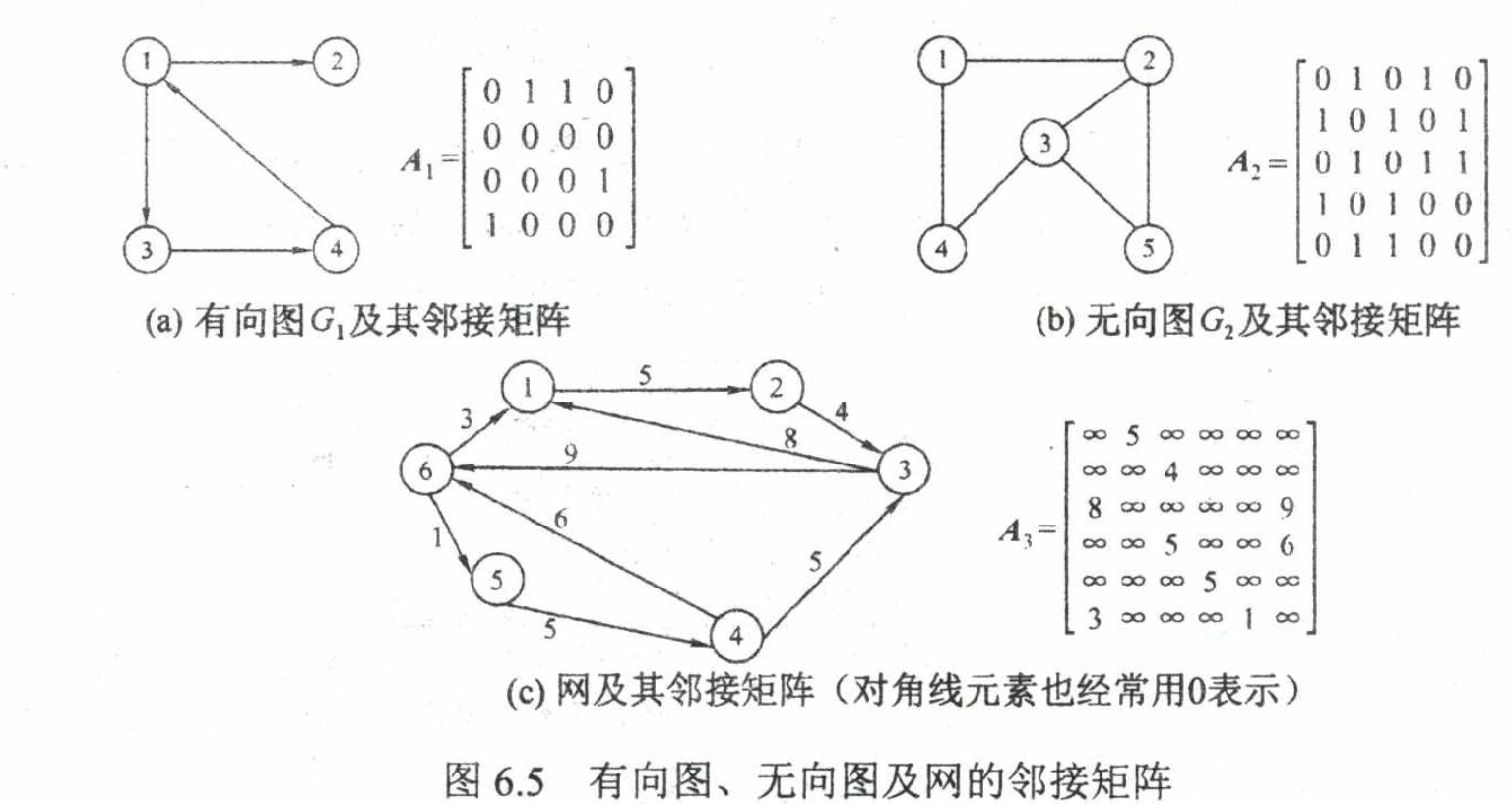
- 对无向图来说,可以用上三角矩阵储存边,其第i行或列的边数量就是顶点i的度
- 对有向图来说,第i行非零元素的个数正好是顶点i的出度,第i列则是其入度
- 易于检测节点间关系,但边需要遍历
- 适合稠密图
邻接表法
每个顶点V建立一个单链表,第i个单链表中的结点表示依附顶点Vi的边(对于有向图则是以顶点Vi为尾的弧),这个单链表就称为顶点Vi的边表(对于有向图则称为出边表)
同时需要顶点表存储顶点,与边表区分 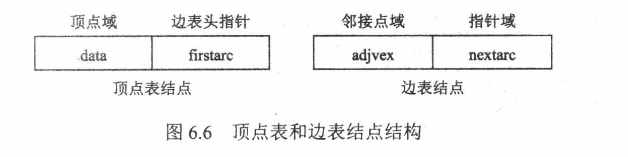
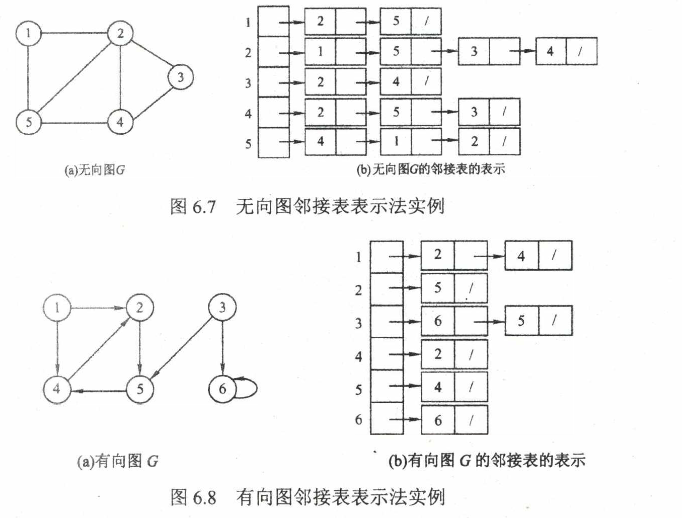
1 |
|
- 无向图的存储空间O(V+2E),有向图是O(V+E)
- 适合稀疏图
- 容易找到一个顶点的所有邻居,但难以判断给定两节点关系
- 求一个给定顶点的出度只需计算其邻接表中的结点个数;但求其顶点的入度则需要遍历全部的邻接表(逆邻接表相反)
- 链接次序任意,因此不唯一
十字链表
有向图的存储结构
在十字链表中,对应于有向图中的每条弧有一个结点,对应于每个顶点也有一个结点,顶点结点之间是顺序存储的
弧结点中:
- tailvex和headvex两个域分别指示弧尾和弧头这两个顶点的编号
- hlink域指向弧头相同的下一个弧结点
- tlink域指向弧尾相同的下一个弧结点
- info域存放该弧的相关信息
- 弧头相同的弧就在同一个链表上,弧尾相同的弧也在同一个链表上
顶点结点中:
- data域存放该顶点的数据信息,如顶点名称
- firstin域指向以该顶点为弧头的第一个弧结点
- firstout域指向以该顶点为弧尾的第一个弧结点
容易求得顶点的出度和入度。图的十字链表表示是不唯一的,但一个十字链表表示确定一个图

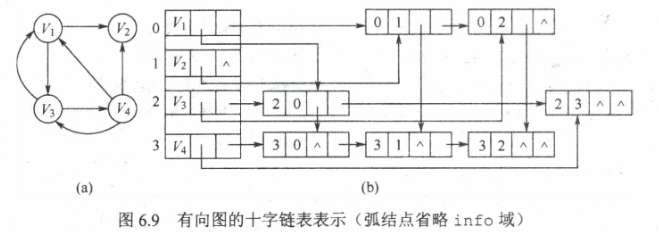
邻接多重表
无向图的存储结构
所有依附于同一顶点的边串联在同一链表中,由于每条边依附于两个顶点,因此每个边结点同时链接在两个链表中
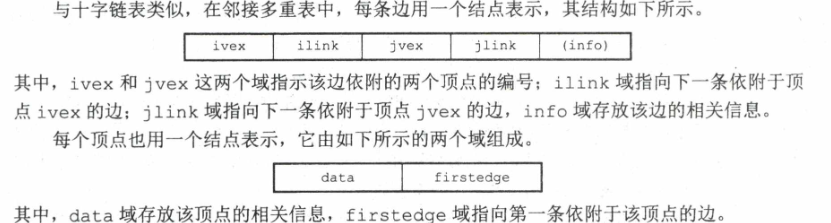
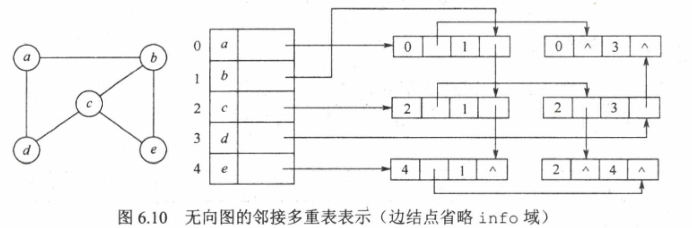
基本操作
- Adjacent (G, x, y):判断图G是否存在边(x,y)
- Neighbors (G, x):列出图G中与结点x邻接的边
- InsertVertex (G, x):在图 G 中插入顶点 x
- DeleteVertex (G, x):从图 G 中删除顶点 x
- AddEdge (G, x, y):若无向边(x,y)或有向边
<x,y>不存在,则向图G中添加该边 - RemoveEdge (G, x, y):若无向边(x,y)或有向边
<x,y>存在,则从图G中删除该边 - FirstNeighbor (G, x):求图G中顶点x的第一个邻接点,若有则返回顶点号。若x没有邻接点或图中不存在x,则返回-1
- NextNeighbor (G, x, y):假设图G中顶点y是顶点x的一个邻接点,返回除y外顶点x的下一个邻接点的顶点号,若y是x的最后一个邻接点,则返回-1
- Get_edge_value (G, x, y):获取图G中边(x,y)或对应的权值
- Set_edge_value (G, x, y, v):设置图G中边(x,y)对应的权值为v
- 有向图的邻接表存储结构中,顶点V在边表中出现的次数是顶点v的入度(题中的边表不包括顶点表,任何顶点u对应的边表中存放的都是以u为起点的边所对应的另一个顶点V)
- 邻接矩阵\(A^m\)的i行j列节点的值,是i节点到j节点长度为m的路径数
遍历
BFS/DFS中邻接表的时间复杂度是O(V+E),邻接矩阵的时间复杂度是O(\(V^2\))
- 广度遍历是分层查找,需要使用队列
- 邻接矩阵查找每个结点的邻边需要O(V)邻接表为O(E)
- 使用BFS可以求解非带权图的单源最短路径问题
- 广度遍历的过程中可以得到一棵遍历树,称为广度优先生成树,其是否唯一取决于邻接表和矩阵存储表示是否唯一
- 深度遍历需要使用栈或者递归
- 基于邻接矩阵的遍历所得到的DFS序列和BFS序列是唯一的,基于邻接表的遍历所得到的DFS序列和BFS序列是不唯一的
- 空间复杂度为O(V)
- 对连通图调用DFS才能产生深度优先生成树,否则会得到森林,这样的生成不唯一
- DFS可以得到一个拓扑排序序列
- 可用于检测环,如果遍历时遇到已经访问的结点,则有环
很容易看出非连通图的遍历可能需要进行多次,一般通过循环实现
hello-algo的比较规范的实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
/* 广度优先遍历 */
// 使用邻接表来表示图,以便获取指定顶点的所有邻接顶点
vector<Vertex*> graphBFS(GraphAdjList& graph, Vertex* startVet) {
// 顶点遍历序列
vector<Vertex*> res;
// 哈希表,用于记录已被访问过的顶点
set<Vertex*> visited = { startVet };
// 队列用于实现 BFS
queue<VNode*> que;
que.push(startVet);
// 以顶点 vet 为起点,循环直至访问完所有顶点
while (!que.empty()) {
Vertex* vet = que.front();
que.pop(); // 队首顶点出队
res.push_back(vet); // 记录访问顶点
// 遍历该顶点的所有邻接顶点
auto adjVet = vet->first;
while (adjVet) {
if (visited.count(adjVet->adjvex)) {
adjVet = adjVet->next;
continue; // 跳过已被访问的顶点
}
que.push(adjVet->adjvex); // 只入队未访问的顶点
visited.emplace(adjVet->adjvex); // 标记该顶点已被访问
adjVet = adjVet->next;
}
}
// 返回顶点遍历序列
return res;
}
/* 深度优先遍历辅助函数 */
void dfs(ALGraph& graph, set<VNode*>& visited, vector<VNode*>& res, VNode* vet) {
res.push_back(vet); // 记录访问顶点
visited.emplace(vet); // 标记该顶点已被访问
// 遍历该顶点的所有邻接顶点
auto adjVet = vet->first;
vector<VNode*> temp = {};
while (adjVet) {
temp.push_back(adjVet->adjvex);
adjVet = adjVet->next;
}
for (auto V : temp) {
if (visited.count(V))
continue; // 跳过已被访问的顶点
dfs(graph, visited, res, V); // 递归访问邻接顶点
}
}
/* 深度优先遍历 */
// 使用邻接表来表示图,以便获取指定顶点的所有邻接顶点
vector<VNode*> graphDFS(ALGraph& graph, VNode* startVet) {
// 顶点遍历序列
vector<VNode*> res;
// 哈希表,用于记录已被访问过的顶点
set<VNode*> visited;
dfs(graph, visited, res, startVet);
return res;
}
应用
最小生成树
生成树是指一个图连接所有节点的,且边数为n-1的子图
边的权值之和最小的生成树即为图的最小生成树,树形不唯一,但权值的和唯一(即所有权值不相等时树形也唯一)
有多种算法,普遍思路是从最小边开始贪心
- prim算法,由于用c++写出过于复杂,以下仅文字描述
- 加入一个随机未访问节点
- 选取起始顶点已访问,指向顶点未访问的边中权值最小的,加入树
- 重复2.直到访问所有节点
- 时间复杂度O( \(V^2\) ),适合密集图
- Kruskal算法
- 初始化一个边集为空
- 从图取出权值最小的边,若两点不都被访问过,加入边集
- 重复2.直到边集有n-1条边
- 如果用最小堆实现,则复杂度O( \(E\log_{2}E\) ),适合稀疏图
带权图的最短路径
- 迪杰斯特拉算法(猎魔人那个),属于一种贪心算法
- 初始化dist和path数组,前者记录v0到vi的最短路径长,初始化为两者边长或无穷(出发点一般是0);后者记录源点到顶点vi之间的最短路径的前驱结点
- 选出当前已知且未访问过的最短路径终点Vj,标记访问
- 进行所谓的放松操作,就是查看j的可达节点k,经过j的路径是否比dist数组中的
dist[k]小,如果小就更新dist - 重复2.3.一共n-1次,即访问所有节点
- 时间复杂度O(\(V^2\))
- 在加入的过程中,由于每次选最小边,总保持从源点v到已访问顶点集s中各顶点的最短路径长度不大于从源点v到未访问顶点集中任何顶点的最短路径长度,即s中顶点已经求到其最短路径,而负权值会打破这个条件
- Floyd算法
- 设置矩阵序列A0~Ak,其中 \(A^{(k)}[i][j]\) 表示元素i到j,考虑序号小于k的中间节点的最短路径长度,即迭代到n-1时得出整个图的最短路径(节点序号从0索引),k=-1时表示i->j直接路径或正无穷
- 即每次迭代时k+1, \(A^{(k)}[i][j]=\mathrm{Min}\{A^{(k-1)}[i][j],\ A^{(k-1)}[i][k]+A^{(k-1)}[k][j]\},\quad k=0,1,\cdots,n-1\) ,这样每次迭代就多考虑一个中间节点
- 时间复杂度为O( \(V^3\)),但常数系数较小,输入中等规模时很有效,允许图中有带负权值的边,但不允许有包含带负权值的边组成的回路;同样适用于带权无向图
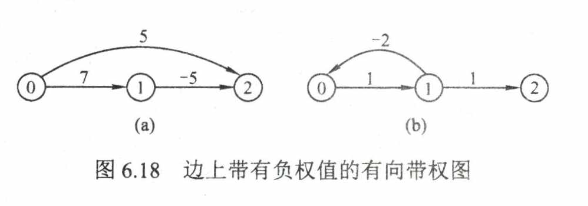
拓扑排序
有向无环图DAG可以用于简化存储空间(dag表示的表达式不可能出现重复的操作数顶点) 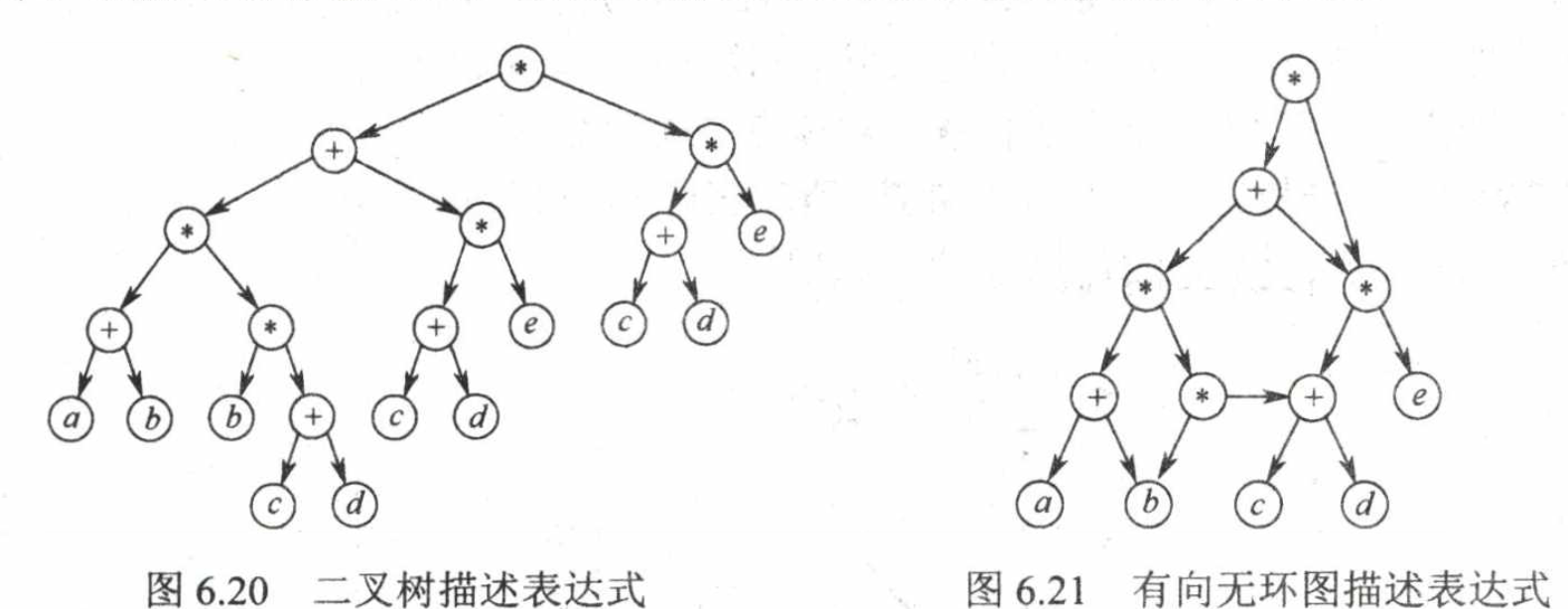
AOV网:若用DAG图表示一个工程,其顶点表示活动,用有向边<Vi,Vj>表示活动Vi必须先于活动Vj,则将这种有向图称为顶点表示活动的网络,记为AOV网.活动Vi是活动Vj的直接前驱,活动Vj是活动Vi的直接后继,这种前驱和后继关系具有传递性,且任何活动不能以它自己作为自己的前驱或后继
一个由DAG图中全部节点构成的无重复序列,且若顶点A在序列中排在顶点B的前面,则在图中不存在从顶点B到顶点A的路径,那么这个序列就是一个拓扑排序
深度遍历会直接产生一个拓扑排序,此外的常见思路:
- 从AOV网中选择一个没有前驱的顶点并输出
- 从网中删除该顶点和所有以它为起点的有向边
- 重复1.和2.直到当前的AOV网为空或当前网中不存在无前驱的顶点为止。后一种情况说明有向图中必然存在环
cpp实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25bool TopologicalSort(ALGraph G, int indegree[]) {
vector<VNode*> res;
stack<VNode*> s;
int i;
for (i = 0;i < G.vexnum;i++)
if (indegree[i] == 0)
s.push(&G.vertices[i]);
int count = 0;
while (!s.empty()) {
VNode* i = s.top();
res.push_back(i);
++count;
s.pop();
ArcNode* p = i->first;//将所有i指向的顶点的入度减1,并且将入度减为0的顶点压入栈S
while (p) {
--indegree[p->adjvex->no];
if (indegree[p->adjvex->no] == 0) s.push(p->adjvex);
p = p->next;
}
}//while
if (count < G.vexnum)
return false; //排序失败,有向图中有回路
else
return true;
}
由于输出每个顶点的同时还要删除以它为起点的边,故采用邻接表存储时拓扑排序的时间复杂度为O(V+E),采用邻接矩阵存储时拓扑排序的时间复杂度为O(\(V^2\))
逆拓扑排序:
- 从AOV网中选择一个没有后继(出度为0)的顶点并输出。
- 从网中删除该顶点和所有以它为终点的有向边。
- 重复1.和2.直到当前的AOV网为空
- 每个顶点有唯一的前驱后继关系时,拓扑排序的结果是唯一的
- 由于AOV网中各顶点的地位平等,每个顶点编号是人为的,因此可以按拓扑排序的结果重新编号,生成AOV网的新的邻接存储矩阵,这种邻接矩阵可以是三角矩阵;但对于一般的图来说,若其邻接矩阵是三角矩阵,则存在拓扑序列;反之则不一定成立
关键路径
带权有向图中,以顶点表示事件,以有向边表示活动,以边上的权值表示完成该活动的开销(如完成活动所需的时间),称之为用边表示活动的网络,简称AOE网
- 只有在某顶点所代表的事件发生后,从该顶点出发的各有向边所代表的活动才能开始
- 只有在进入某顶点的各有向边所代表的活动都已结束时,该顶点所代表的事件才能发生
- AOE网中仅有一个入度为0的顶点,称为开始顶点(源点),它表示整个工程的开始;网中也仅存在一个出度为0的顶点,称为结束顶点(汇点),它表示整个工程的结束
从源点到汇点的所有路径中,具有最大路径长度的路径称为关键路径,而把关键路径上的活动称为关键活动,关键路径代表完成整个工程的最短时间
一些关键名词:
事件vk的最早发生时间ve(k)
\(\nu e(k)=\mathrm{Max}\left\{\nu\mathrm{e}(j)+\mathrm{Weight}(\nu_{j},\,\nu_{k})\right\}\)
vk是vj的任意后缀节点
按从前往后的顺序进行,可以在拓扑排序的基础上计算事件vk的最迟发生时间vl(k)
在不推迟整个工程完成的前提下,即保证它的后继事件vj在其最迟发生时间vl(j)能够发生时,该事件最迟必须发生的时间
\(\nu l(k)=\mathrm{Min}\left\{\nu l(j)-\mathrm{Weight}(\nu_{k},\,\nu_{j})\right\}\)
设一个栈以记录拓扑序列,拓扑排序结束后从栈顶至栈底便为逆拓扑有序序列,可以逆拓扑序列进行vl的计算活动ai的最早开始时间e(i),即该活动弧的起点所表示的事件的最早发生时间,若边
<vk,vj>表示活动ai,则有e(i) = ve(k)活动ai的最迟开始时间l(i),即该活动弧的终点所表示事件的最迟发生时间与该活动所需时间之差。若边
<vk,vj>表示活动ai,则有 \(l(i)=v l(j)-\operatorname{Weight}(\nu_{k},\,\nu_{j})\)一个活动ai的最迟开始时间l(i)和其最早开始时间e(i)的差d(i)=l(i)-e(i)
指该活动完成的时间余量,为0的活动需要立即完成,称为关键活动
- 从源点出发,令ve(源点)= 0,按拓扑有序求其余顶点的最早发生时间ve()
- 从汇点出发,令vl(汇点)= ve(汇点),按逆拓扑有序求其余顶点的最迟发生时间vl()
- 根据各顶点的ve()值求所有弧的最早开始时间e()
- 根据各顶点的vl()值求所有弧的最迟开始时间l()
- 求AOE网中所有活动的差额d(),找出所有d() = 0的活动构成关键路径
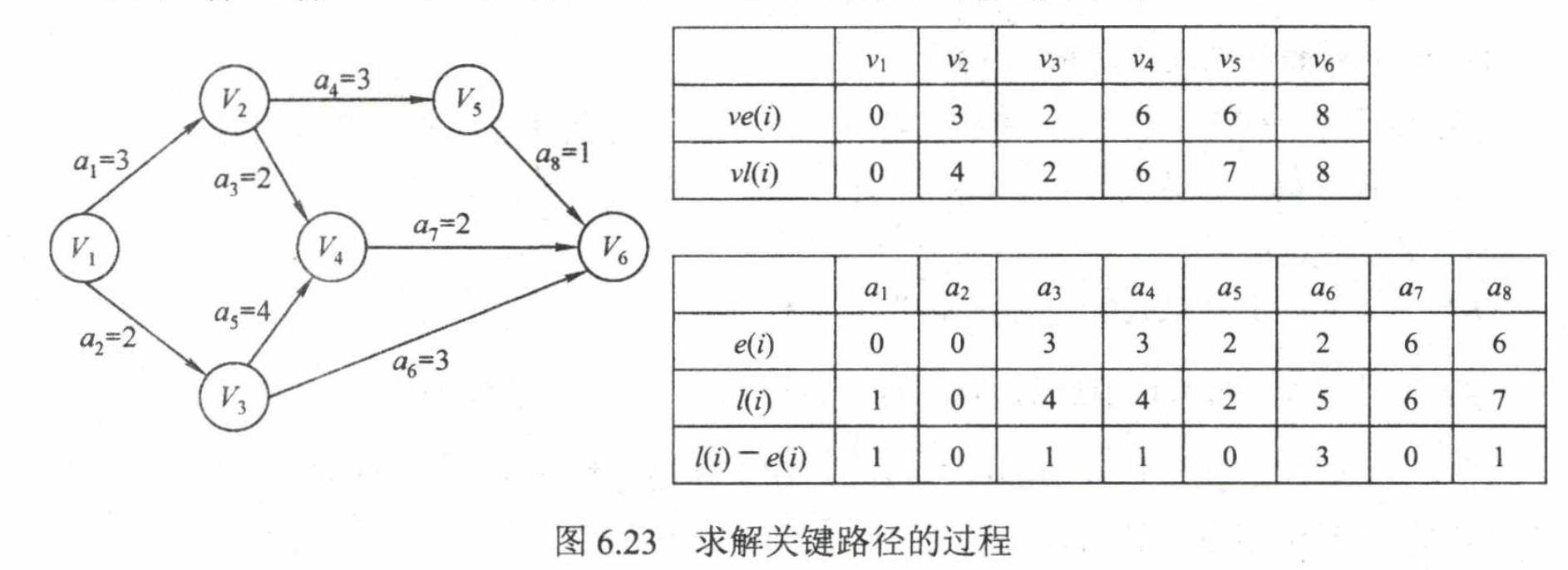 关键路径上的所有活动都是关键活动,网中的关键路径并不唯一,加快那些包括在所有关键路径上的关键活动才一定能达到缩短工期的目的
关键路径上的所有活动都是关键活动,网中的关键路径并不唯一,加快那些包括在所有关键路径上的关键活动才一定能达到缩短工期的目的
- 若一个有向图的顶点不能排成一个拓扑序列,则含有顶点数大于1的强连通分量
- 对有向图中的顶点适当地编号,使其邻接矩阵为三角矩阵且主对角元全为零的充分必要条件是,该有向图可以进行拓扑排序
查找
- 在数据集合中寻找满足某种条件的数据元素的过程称为查找
- 用于查找的数据集合称为查找表,根据是否可以增加删除元素分为静态和动态
- 数据元素中唯一标识该元素的某个数据项的值是关键字
- 一次查找的长度是指需要比较的关键字次数,而平均查找长度则是所有查找过程中进行关键字的比较次数的平均值,定义为:\(\mathrm{ASL}=\sum_{i=1}^{n}P_{i}C_{i}\)
- 用于指示查找边界的特殊数据元素称为哨兵,例如数组末尾放置一个正无穷表示结束
给定n个元素的线性表,定位第i个元素时,需进行n-i + 1次比较,设n是查找表的长度;Pi是查找第i个数据元素的概率,一般认为每个数据元素的查找概率相等,即Pi=1/n; Ci是找到第i个数据元素所需进行的比较次数,平均长度为:
\(\mathrm{ASL}_{\mathrm{成功}}=\sum_{i=1}^{n}P_{i}(n-i+1)\)
每个元素查找概率相等时:
\(\mathrm{ASL}_{成功}=\sum_{i=1}^{n}P_{i}(n-i+1)=\frac{n+1}{2}\)
不成功时,查找长度是n+1
基本分类
顺序查找
查找成功的平均查找长度和一般线性表的顺序查找一样
对有序表来说,查找失败的平均查找长度:
\(\mathrm{ASL}_{不成功}=\sum_{j=1}^{n}q_{j}(l_{j}-1)={\frac{1+2+\cdots+n+n}{n+1}}={\frac{n}{2}}+{\frac{n}{n+1}}\)
其中\(q_j\)是到达第j个失败节点的概率,相等概率时为 \(\frac{1}{n+1}\) \(l_j\)是第j个失败节点所在判断树的层数
可以是链式存储结构
二分查找
概念略,其判断树是平衡二叉树,平均查找长度:
\(\operatorname{ASL}={\frac{1}{n}}\sum_{i=1}^{n}l_{i}={\frac{1}{n}}(1\times1+2\times2+\cdots+h\times2^{h-1})={\frac{n+1}{n}}\log_{2}(n+1)-1\approx\log_{2}(n+1)-1\)
最大查找长度: \(\lceil\log_2^{n+1}\rceil\) 也是查找不成功时的比较次数 其中h是树高
分块查找
分为彼此间有顺序关系,但内部无序的块,平均查找长度为索引查找和块内查找的平均长度之和
将长度为n的查找表均匀地分为b块,每块有s个记录,等概率的情况下:
\(s={\sqrt{n}}\)时,取最小值 \({\sqrt{n}}+1\)
- 折半查找过程所对应的判定树是平衡二叉树,左右子树高度相差最多为1
- 根据上一条可推断,查找失败时,比较次数最多相差1
使用树的查找
BST
对二叉排序树BST进行中序遍历,可以得到一个递增的有序序列
查找效率取决于是否平衡
基本操作:
- 查找
- 从根节点出发,根据当前节点与key大小关系向下前进
- 找到或进入空节点时,返回当前节点
- 插入
- 类似查找,但记录前驱节点
- key和当前节点重合时,直接退出
- 正常应前进到空节点,此时根据key与pre节点的大小关系决定插入点
- 删除(最复杂)
- 类似查找,但记录前驱
- 查找无结果时,直接退出
- 找到后分两种情况
- 0或1一个孩子,优先和存在的孩子交换,然后删除即可
- 2个孩子,遍历右子树的最左节点(相反也行),和当前节点交换,然后(递归)删除交换后对应子树的待删除节点
c++实现: 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102/* 查找节点 */
TreeNode* search(TreeNode* root, int num) {
TreeNode* cur = root;
// 循环查找,越过叶节点后跳出
while (cur != nullptr) {
// 目标节点在 cur 的右子树中
if (cur->data < num)
cur = cur->right;
// 目标节点在 cur 的左子树中
else if (cur->data > num)
cur = cur->left;
// 找到目标节点,跳出循环
else
break;
}
// 返回目标节点
return cur;
}
/* 插入节点 */
void insert(TreeNode* root, int num) {
// 若树为空,则初始化根节点
if (root == nullptr) {
root = new TreeNode(num);
return;
}
TreeNode* cur = root, * pre = nullptr;
// 循环查找,越过叶节点后跳出
while (cur != nullptr) {
// 找到重复节点,直接返回
if (cur->data == num)
return;
pre = cur;
// 插入位置在 cur 的右子树中
if (cur->data < num)
cur = cur->right;
// 插入位置在 cur 的左子树中
else
cur = cur->left;
}
// 插入节点
TreeNode* node = new TreeNode(num);
if (pre->data < num)
pre->right = node;
else
pre->left = node;
}
/* 删除节点 */
void remove(TreeNode* root, int num) {
// 若树为空,直接提前返回
if (root == nullptr)
return;
TreeNode* cur = root, * pre = nullptr;
// 循环查找,越过叶节点后跳出
while (cur != nullptr) {
// 找到待删除节点,跳出循环
if (cur->data == num)
break;
pre = cur;
// 待删除节点在 cur 的右子树中
if (cur->data < num)
cur = cur->right;
// 待删除节点在 cur 的左子树中
else
cur = cur->left;
}
// 若无待删除节点,则直接返回
if (cur == nullptr)
return;
// 子节点数量 = 0 or 1
if (cur->left == nullptr || cur->right == nullptr) {
// 当子节点数量 = 0 / 1 时, child = nullptr / 该子节点
TreeNode* child = cur->left != nullptr ? cur->left : cur->right;
// 删除节点 cur
if (cur != root) {
if (pre->left == cur)
pre->left = child;
else
pre->right = child;
}
else {
// 若删除节点为根节点,则重新指定根节点
root = child;
}
// 释放内存
delete cur;
}
// 子节点数量 = 2
else {
// 获取中序遍历中 cur 的下一个节点
TreeNode* tmp = cur->right;
while (tmp->left != nullptr) {
tmp = tmp->left;
}
int tmpVal = tmp->data;
// 递归删除节点 tmp
remove(root, tmp->data);
// 用 tmp 覆盖 cur
cur->data = tmpVal;
}
}
平衡二叉树AVL(Balanced Binary Tre)
平衡二叉树的定义:
- 一棵空树
- 具有下列性质的二叉树
- 它的左子树和右子树都是平衡二叉树
- 左子树和右子树的高度差的绝对值不超过1
定义结点左子树与右子树的高度差为该结点的平衡因子,则平衡二叉树结点的平衡因子的值只可能是-1、0或1
1 | /* AVL 树节点类 */ |
旋转
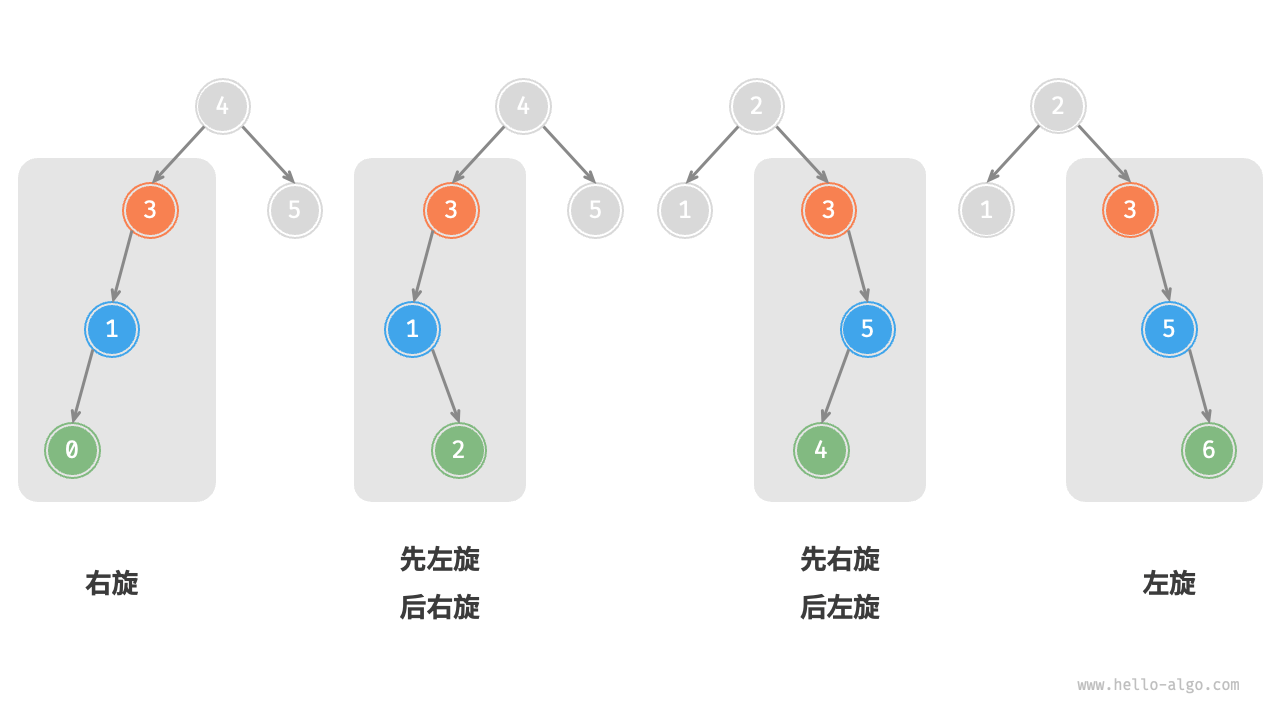
- 右旋LL:失衡节点的左子树加入新节点高度+1,失衡因子达到2
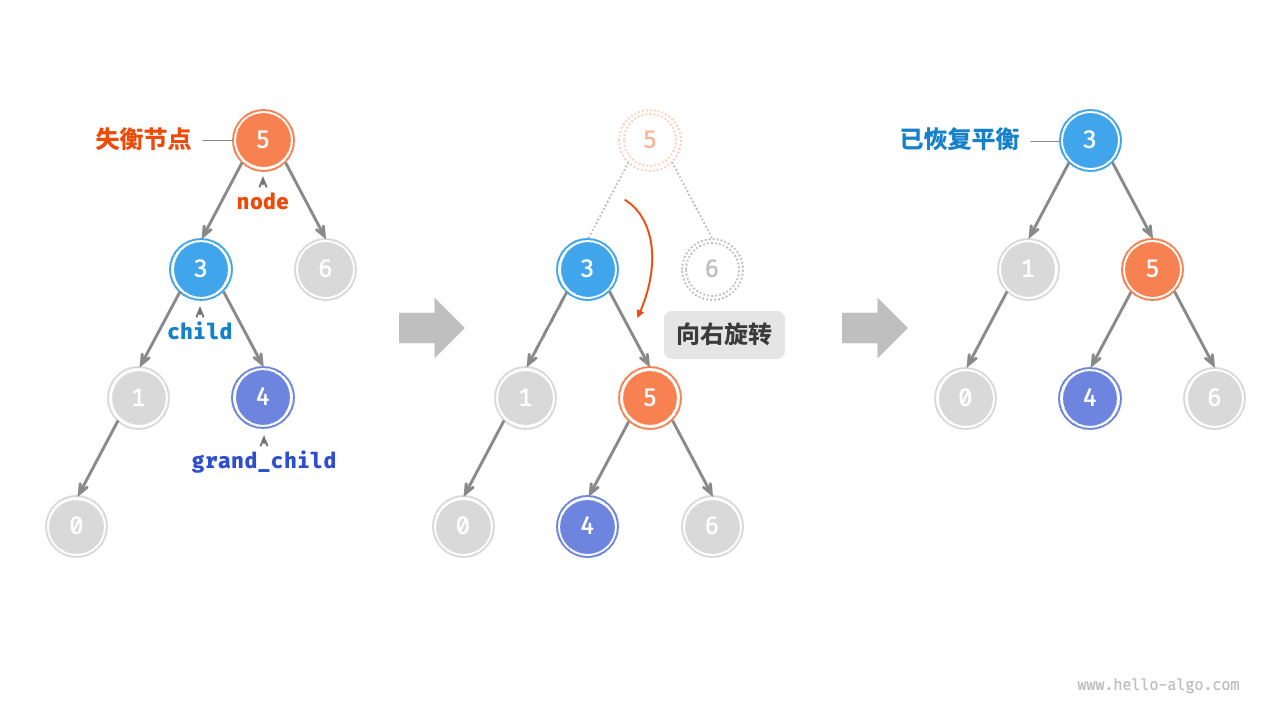
- 左旋RR:右旋的镜像
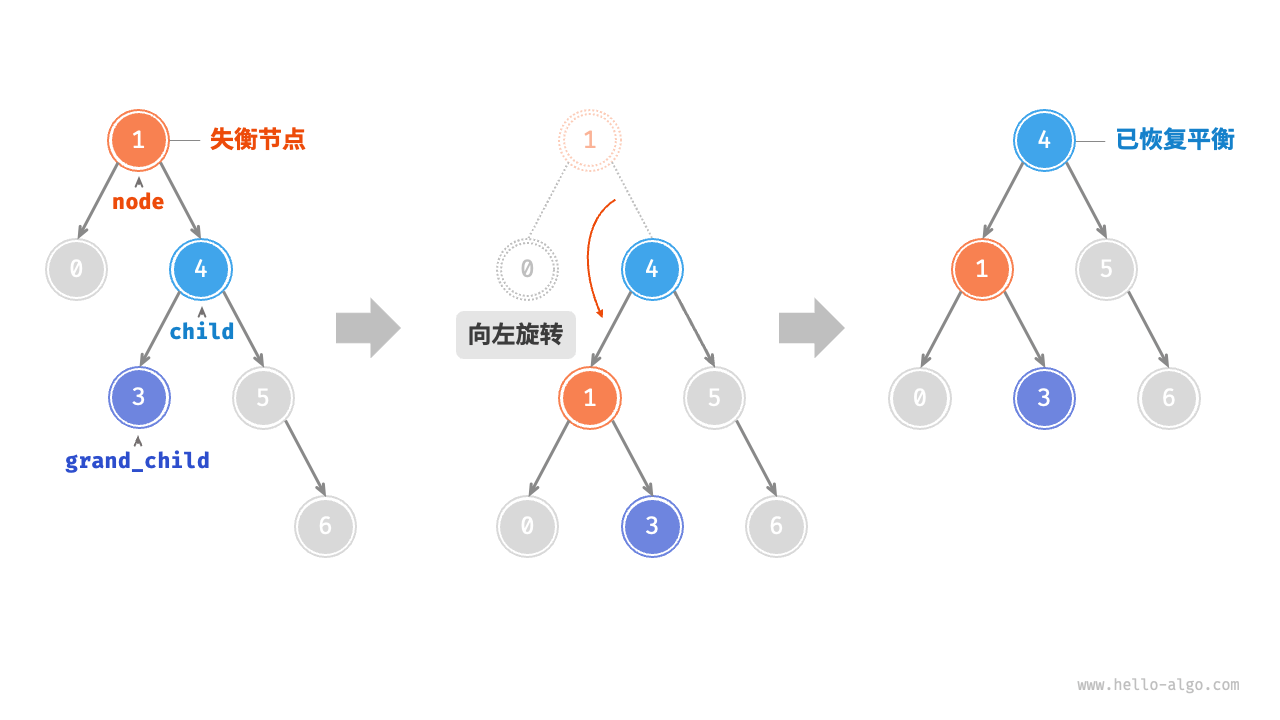
- 先左旋后右旋LR: 失衡节点左倾,其子节点右倾
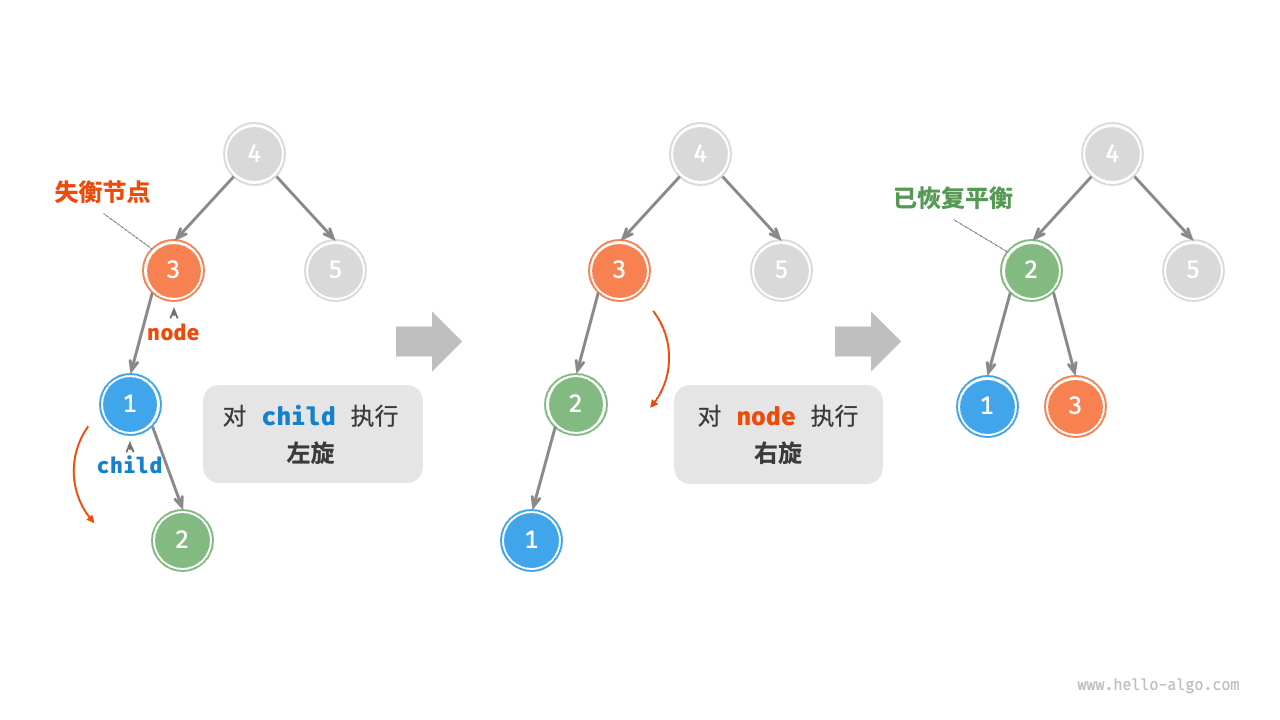
- 先右旋后左旋RL:LR的镜像
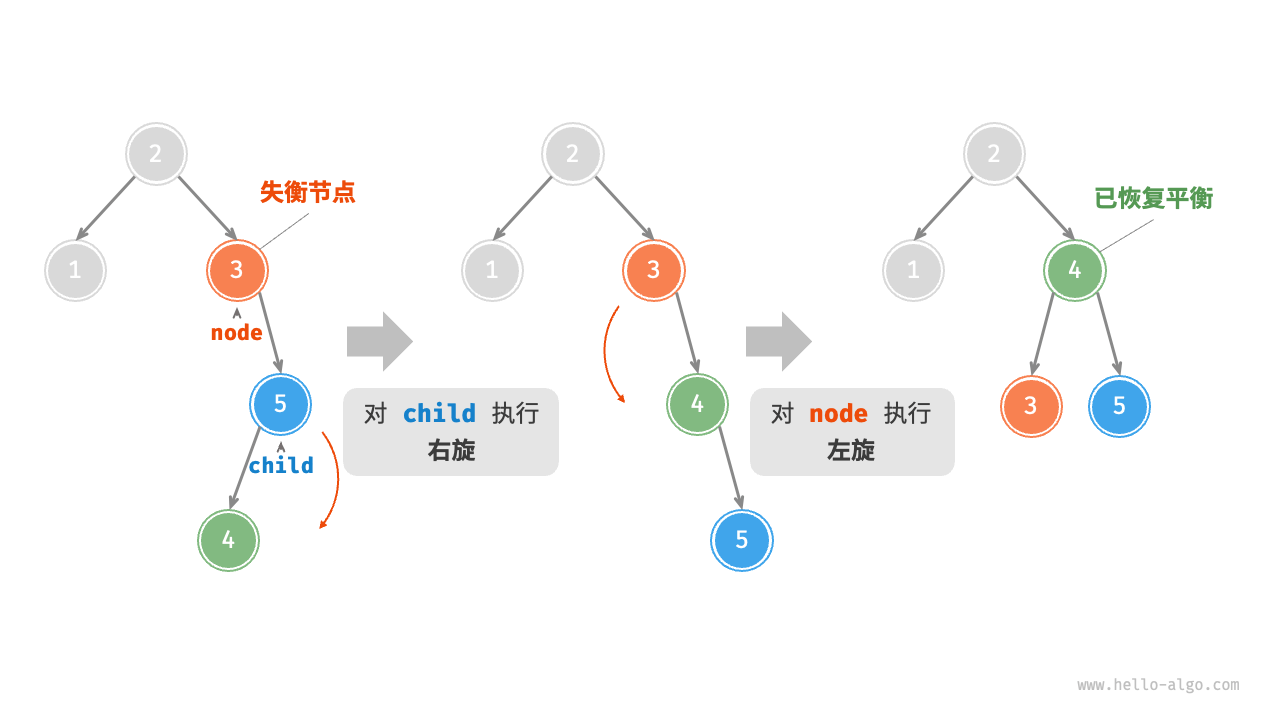
| 失衡节点平衡因子 | 子节点平衡因子 | 旋转方法 |
|---|---|---|
| >1 | ≥0 | 右旋 |
| >1 | <0 | 先左旋后右旋 |
| < -1 | ≤0 | 左旋 |
| < -1 | >0 | 先右旋后左旋 |
常见操作
- 插入:类似BST,唯一的区别在于,在 AVL 树中插入节点后,从该节点到根节点的路径上可能会出现一系列失衡节点。因此从该节点开始,自底向上执行旋转操作,使所有失衡节点恢复平衡
- 删除:类似BST,在BST的删除节点方法的基础上,需要从底至顶执行旋转操作(或者从找到的第一个不平衡子树开始向上),使所有失衡节点恢复平衡
- 构造:执行n次插入
红黑树
满足如下红黑性质的二叉排序树:
- 每个结点或是红色,或是黑色的.
- 根结点是黑色的.
- 叶结点(虚构的外部结点、NULL结点)都是黑色的。
- 不存在两个相邻的红结点(即红结点的父结点和孩子结点均是黑色的)。
- 对每个结点,从该结点到任意一个叶结点的简单路径上,所含黑结点的数量相同。
性质:
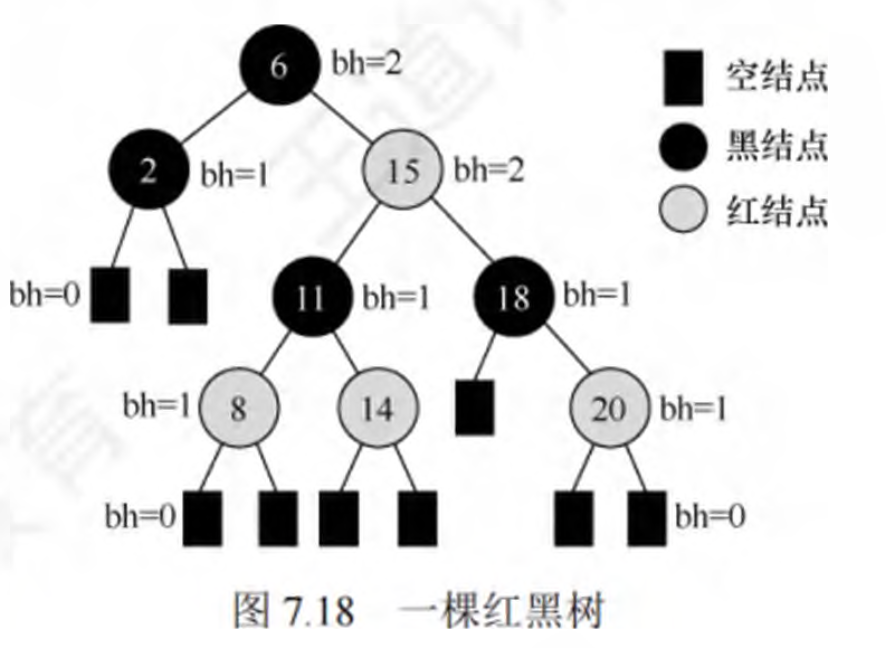
- 从某结点出发(不含该结点)到达一个叶结点的任意一个简单路径上的黑结点总数称为该结点的黑高(记为bh),黑高的概念是由性质5确定的;根结点的黑高称为红黑树的黑高
- 从根到叶结点的最长路径不大于最短路径的2倍
- 由5.从根到任意一个叶结点的简单路径最短时,这条路径必然全由黑结点构成
- 由4.某条路径最长时,这条路径必然是由黑结点和红结点相间构成的
- 有n个内部结点的红黑树的高度 h≤2 $ log_2^{n+1} $
- 从根到叶结点(不含叶结点)的任何一条简单路径上都至少有一半是黑结点,因此,根的黑高至少为h/2,因此 $ n≥2^{h/2}-1 $ (可以数学归纳法证明)
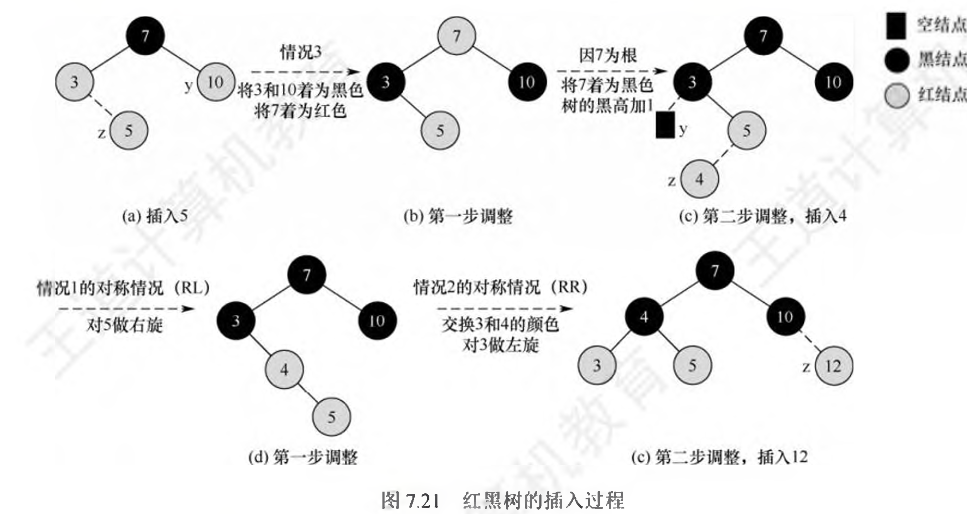
- 新插入红黑树中的结点z初始着为红色,过程:
- 若新插入结点z的父结点是黑色的,无须做任何调整,此时就是一棵标准的红黑树
- 若结点z是根结点,则将z着为黑色(树的黑高增1)
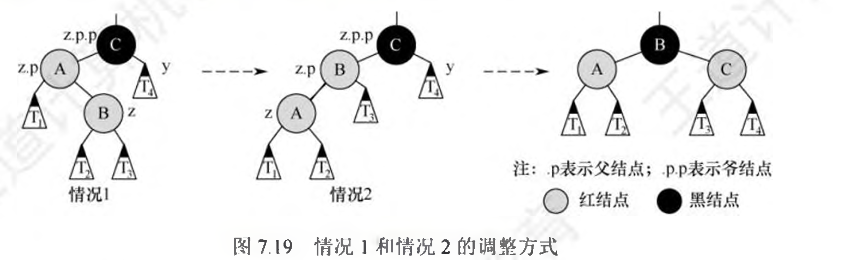
- 若结点z不是根结点,且z的父结点z.p是红色的:
- 若z的叔结点y是黑色的,且z是一个右孩子:先左旋,再右旋
- 若z的叔结点y是黑色的,且z是一个左孩子:右单旋
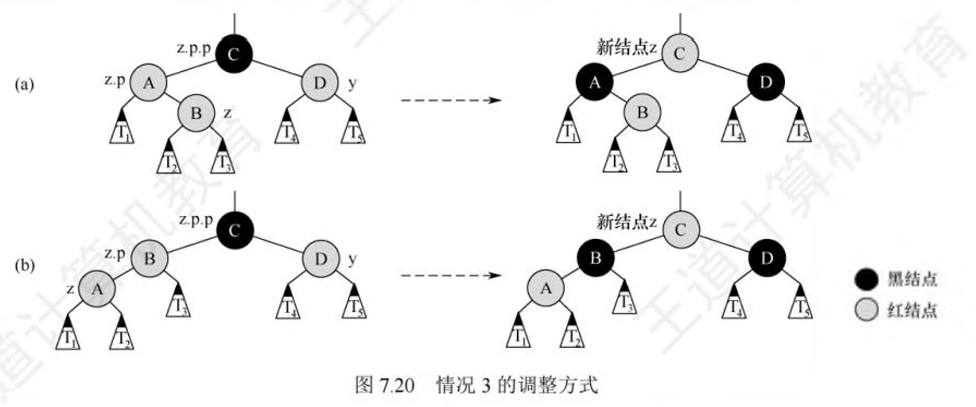
- 若z的叔结点y是红色的:将z.p和y都着为黑色,将z.p.p着为红色;然后,把z.p.p作为新结点z来重复循环,指针z在树中上移两层
红黑树任意一个结点左右子树的高度,相差不超过2倍(例如C++中的map和set;Java中的TreeMap和TreeSet用红黑树实现)
B树
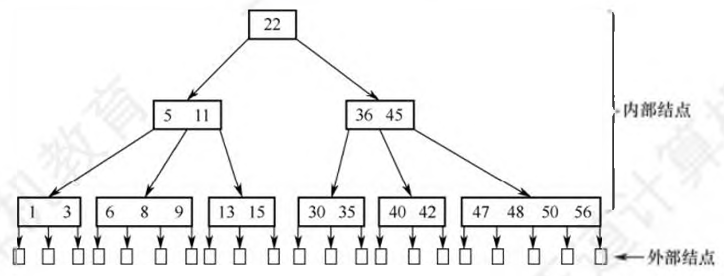
m阶B树是所有结点的平衡因子均等于0的m路平衡查找树
一棵m阶B树或为空树,或为满足如下特性的叉树:
- 树中每个结点至多有m棵子树,即至多有m-1个关键字
- 若根结点不是叶结点,则至少有2棵子树,即至少有1个关键字
- 除根结点外的所有非叶结点至少有 \(\lceil m/2 \rceil\) 棵子树,即至少有 \(\lceil m/2 \rceil -1\) 个关键字
- 所有的叶结点.都出现在同一层次上,并且不带信息(可以视为外部结点或类似于折半查找判定树的失败结点,实际用空指针表示)
- 所有非叶结点的结构如下:
| n | P0 | K1 | P1 | K2 | P2 | …… | Kn | Pn |
|---|
其中:
- Ki为结点的关键字,且从K1至Kn递增
- Pi(从0开始)为指向子树根结点的指针,即指针数为关键字数+1
- P(i-1)所指子树中所有结点的关键字均小于Ki
- Pi所指子树中所有结点的关键字均大于Ki
- \(n\ \left(\lceil m/2\rceil-1\leqslant n\leqslant m-1\right)\) 为结点中关键字的个数
常见操作
查找:
- 在B树中找结点(常在磁盘,找到后读入内存)
- 在结点内找关键字(常在内存)
磁盘存取次数(高度): B树中的大部分操作所需的磁盘存取次数与B树的高度成正比
若n≥1,则对任意一棵包含n个关键字、高度为h、阶数为m的B树:
- 若让每个结点中的关键字个数达到最多,则容纳同样多关键字的B树的高度达到最小
- 关键字的个数满足 \(n\leq(m-1)(1+m+m^{2}+\cdots+m^{h-1})=m^{h}-1\)
- h满足 \(h\geq\log_{m}(n+1)\)
- 若让每个结点中的关键字个数达到最少,则容纳同样多关键字的B树的高度达到最大
- 对查找不成功的节点满足 \(n+1\geq2(\lceil m/2\rceil)^{h-1}\)
- h满足 \(h\leq\log\lceil_{m/2}\rceil((n+1)/2)+1\)
插入:
- 查找算法找出插入该关键字的终端结点
- 每个非根结点的关键字个数都有范围 \([\lceil~m/2\rceil-1,~m-1]\)
- 若结点插入后的关键字个数小于m,可以直接插入
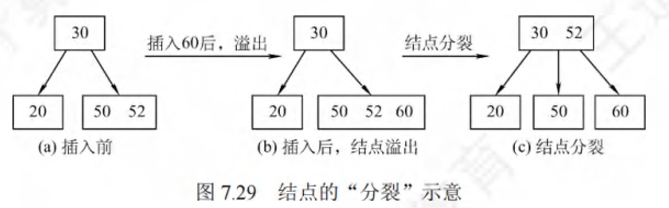
- 若结点插入后的关键字个数大于m-1,对结点进行分裂
- 取一个新结点,在插入key后的原结点,从中间位置 \(\lceil m/2 \rceil\) 将其中的关键字分为两部分,左半留在原结点,右半给新结点,中间位置结点插入原结点的父结点
- 若导致其父结点的关键字个数也超过了上限,则继续进行这种分裂操作,直至这个过程传到根结点为止,进而导致B树高度增1
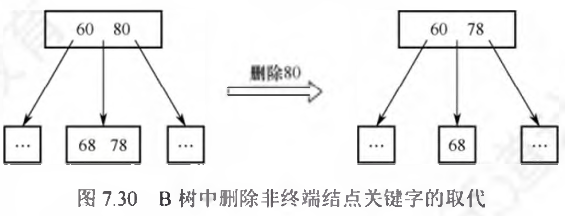
删除:
- 被删关键字k不在终端结点中时,用k的前驱或者后继替代k,并在来源结点删除这个替代元素
- 被删关键字k在终端结点中时
- 若k所在结点删除前的关键字个数 $ ≥m/2 $ ,则可直接删除该关键字
- k所在结点删除前的关键字个数 $ =m/2 $, 该结点相邻节点关键字个数 $ ≥m/2 $,则借一个兄弟的结点过来(先父子换位,然后借一个兄弟给父结点)
- k所在结点删除前的关键字个数 $ =m/2 $, 该结点相邻节点关键字个数 $ =m/2 $ ,将关键字删除后与左(或右)兄弟结点及双亲结点中的关键字进行合并
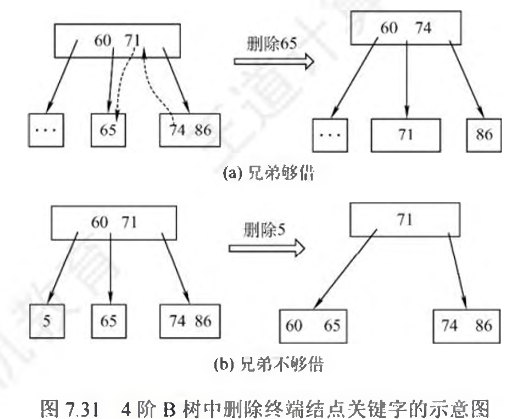
若其双亲结点是根结点且关键字个数减少至0(根结点关键字个数为1时,有2棵子树),则直接将根结点删除,合并后的新结点成为根;
若双亲结点不是根结点,且关键字个数减少不满足要求,则向上递归直到满足要求
B+树
B+树是应数据库所需而出现的一种B树的变形
一棵m阶B+树应满足下列条件:
- 每个分支结点最多有m棵子树(孩子结点)
- 非叶根结点至少有两棵子树,其他每个分支结点至少有 \(\lceil m/2 \rceil\) 棵子树
- 结点的子树个数与关键字个数相等
- 所有叶结点包含全部关键字及指向相应记录的指针,叶结点中将关键字按大小顺序排列,并且相邻叶结点按大小顺序相互链接起来(支持顺序查找)
- 所有分支结点(可视为索引的索引)中仅包含它的各个子结点(即下一级的索引块)中关键字的最大值及指向其子结点的指针
m阶B+树与m阶B树的主要差异:
- 在B+树中,具有n个关键字的结点只含有n棵子树,即每个关键字对应一棵子树;而在B树中,具有n个关键字的结点含有n+1棵子树
- 在B+树中,每个结点(非根内部结点)的关键字个数范围是[ \(\lceil m/2 \rceil\) , m ] (非叶根节点是
[2,m]) ;B树中,每个结点(非根内部结点)的关键字个数n的范围是 [ \(\lceil m/2 \rceil\) -1 , m - 1 ] (根节点是[1,m-1]) - B+树中,叶结点包含了全部关键字,非叶结点中出现的关键字也会出现在叶结点中;而在B树中,最外层的终端结点包含的关键字和其他结点包含的关键字是不重复的
- 在B+树中,叶结点包含信息,所有非叶结点仅起索引作用,非叶结点的每个索引项只含有对应子树的最大关键字和指向该子树的指针,不含有对应记录的存储地址。这样能使一个磁盘块存储更多的关键字,使得磁盘读/写次数更少,查找速度更快
- 在B+树中,用一个指针指向关键字最小的叶结点,将所有叶结点串成一个线性链表
注: 非叶根结点指孩子不为空的根结点
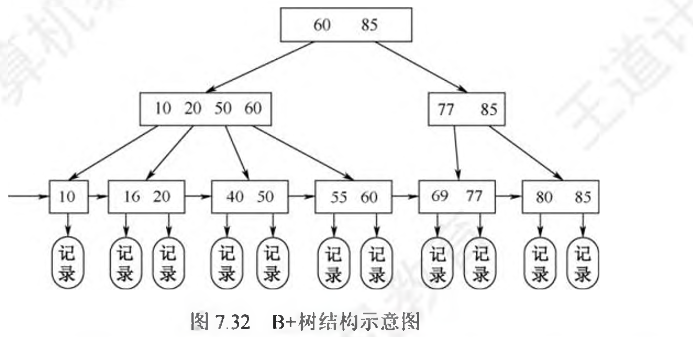
通常有两个头指针:一个指向根结点,另一个指向关键字最小的叶结点;因此可以从最小关键字开始顺序查找或者从根结点开始多路查找
B+树的查找、插入和删除操作和B树的基本类似。只是在查找过程中,非叶结点上的关键字值等于给定值时并不终止,而是继续向下查找,直到叶结点上的该关键字为止
在B+树中,无论查找成功与否,每次查找都是一条从根结点到叶结点的路径
字符串匹配KMP算法

首先,字符串"BBC ABCDAB ABCDABCDABDE"的第一个字符与搜索词"ABCDABD"的第一个字符,进行比较。因为B与A不匹配,所以搜索词后移一位

因为B与A不匹配,搜索词再往后移

就这样,直到字符串有一个字符,与搜索词的第一个字符相同为止

接着比较字符串和搜索词的下一个字符,还是相同

直到字符串有一个字符,与搜索词对应的字符不相同为止

最自然的反应是,将搜索词整个后移一位,再从头逐个比较。这样可行,但效率很差,因为要把"搜索位置"移到已经比较过的位置,重比一遍

当空格与D不匹配时,我们知道前面六个字符是"ABCDAB"。KMP算法的想法是,设法利用这个已知信息,不要把"搜索位置"移回已经比较过的位置,继续把它向后移,这样就提高了效率

怎么做到这一点呢?可以针对搜索词,算出一张《部分匹配表》(Partial Match Table)

已知空格与D不匹配时,前面六个字符"ABCDAB"是匹配的。查表可知,最后一个匹配字符B对应的"部分匹配值"为2,因此按照下面的公式算出向后移动的位数:
移动位数 = 已匹配的字符数 - 对应的部分匹配值
因为 6 - 2 等于4,所以将搜索词向后移动4位

因为空格与C不匹配,搜索词还要继续往后移。这时,已匹配的字符数为2("AB"),对应的"部分匹配值"为0。所以,移动位数 = 2 - 0,结果为 2,于是将搜索词向后移2位
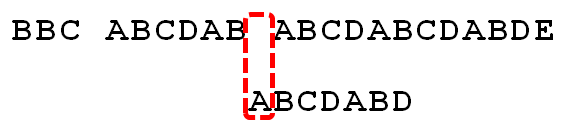
因为空格与A不匹配,继续后移一位

逐位比较,直到发现C与D不匹配。于是,移动位数 = 6 - 2,继续将搜索词向后移动4位

逐位比较,直到搜索词的最后一位,发现完全匹配,于是搜索完成。如果还要继续搜索(即找出全部匹配),移动位数 = 7 - 0,再将搜索词向后移动7位,这里就不再重复了
 前缀指除最后一个字符以外,字符串的所有头部子串;后缀指除第一个字符外,字符串的所有尾部子串;"部分匹配值"是"前缀"和"后缀"的最长的共有元素的长度
前缀指除最后一个字符以外,字符串的所有头部子串;后缀指除第一个字符外,字符串的所有尾部子串;"部分匹配值"是"前缀"和"后缀"的最长的共有元素的长度
如'ababa'的前缀{a,ab,aba,abab} ∩ 后缀{a,ba,aba,baba} = {a,aba},公共元素有两个,最长相等前后缀长度为3
部分匹配值i号表项则是对[0-i]索引的字符串的部分匹配值
对前后缀匹配可以这样理解:
- 如果一位都不匹配,直接跳到下一个字符
- 匹配了n位时,相当于这n位子串是对的,而对这个子串来说的部分匹配值表示从后面数,有个子串和前缀这个匹配正确的子串一样,因此跳转到后缀子串肯定保留着n位匹配的性质。此时,移动位数 = 已匹配的字符数 - 对应的部分匹配值
- 当第n+1位匹配失败时,如果这时移动少于kmp规定的移动次数也能匹配上,那么就会与部分匹配表矛盾
- 此时我们知道前n位匹配,第n+1位不匹配,若移动次数少于规定,那么肯定不会移到最大的公共前后缀上,也就是不会完全匹配上
- 使用反证法,假设移动次数少于规定还能完全匹配,那么字符串在最长公共后缀前的一个子串可以匹配前缀,这个匹配前缀的子串又成了新的最长公共后缀,与定义矛盾
将next数组右移一位,最左侧填-1,则匹配中每次右移位数=j-1-next[j]为了方便也可以+1
求next数组可视为以下递归过程:
- 已知
next[j]=k,即前j-1个元素中前k-1(next右移过一位且整体+1)个元素和后k-1个元素相同,j+1分为以下两种情况- pk=pj,
next[j+1]=next[j]+1 - pk!=pj,目前
p1~pj-1部分已知有k-1长度的公共前后缀(因为next加过1),但无法和pj匹配,因此在1~k-1找一个更小的公共前后缀(肯定要公共前后缀才能继续接上pj),即k=next[k],看这个更小的前公共子序列能否和pj组成更大的公共序列,如此重复- 也就是说,要求
next[j+1],当pj匹配不上pk时,查next[j]会得到j前面部分的公共前后缀长度k-1,下一个有可能匹配上的就是前面的公共前缀[1~k-1]后面第一个元素( \(p_{next[next[j]]}\) 即 \(p_{next[k]}\) )与pj,如果这次还匹配不上,就继续递归
- 也就是说,要求
- pk=pj,
next的优化:由于每次右移next[j],即下一个比较的一直是p[next[j]],如果和p[j]相同,则这样的比较没有意义,因此对相等的pj和p_next[j]要不断将next[j]修正为next[next[j]];更新后的数组命名为nextval
时间复杂度O是(m+n)
1 |
|
哈希
散列函数:一个把查找表中的关键字映射成该关键字对应的地址的函数,记为Hash(key)=Addr
散列函数可能会把两个或两个以上的不同关键字映射到同一地址,称这种情况为“冲突”,这些发生碰撞的不同关键字称为同义词。
应满足以下条件:
- 定义域必须包含全部需要存储的关键字,而值域的范围则依赖于散列表的大小或地址范围
- 计算出来的地址应该能等概率、均匀地分布在整个地址空间中,从而减少冲突
- 应尽量简单
常见的哈希函数:
- 直接定址法,直接取关键字的某个线性函数值为散列地址:\(H(\mathrm{key})=a\times \mathrm{key}+b\)
- 除留余数法,取不超过且尽可能接近表长m的质数p,\(H(\mathrm{key})=\mathrm{key}\ \% p\)
- 数字分析法,选取r进制的r个数码分布较为均匀的若干位作为散列地址
- 平方取中法,取关键字的平方值的中间几位作为散列地址
冲突处理
- 开放寻址,\(H_{i}=(H(\mathrm{key})+d_{i})\%m\) 其中 \(d_i\) 为增量序列,删除需要特殊标记(i从1开始),再散列方法(第一次散列失败后开始使用)如下:
- 线性探测法,di为
[1,m-1](循环,但下一次循环从0开始),遇到连续元素时效率较低 - 平方探测法,di为 \(0^2,1^2,-1^2,……,-k^2\) ,其中
k<=m/2,散列表长度m必须是一个可以表示成4k + 3的素数,又称二次探测法;可以避免出现“堆积”问题,缺点是不能探测到散列表上的所有单元,但至少能探测到一半单元 - 双散列法,\(d_{i}=\operatorname{Hash}_{2}(key)\),即 \(H_{i}=(H(\mathrm{key})+i\times\mathrm{Hash}_{2}(\mathrm{key}))\ \% \,m\) (i从0开始)
- 伪随机序列法,di为伪随机序列
- 线性探测法,di为
- 链接(拉链)法,映射相同哈希值的元素形成链表
哈希表的装载因子α=n/m,影响平均查找和删除时间,假设均匀散列,插入元素(需要一次查找失败)至多期望1/(1-α)次查找
- 查找的初始情况由散列函数可能的哈希值决定,例如mod的分母
排序
408设计的排序基本是将给定序列规律化。输入是线性表
稳定性:若输入两元素key相等,输出序列若两者相对顺序不变,则该算法稳定,否则不稳定
- 内部排序,是指在排序期间元素全部存放在内存中的排序
- 外部排序,是指在排序期间元素无法全部同时存放在内存中,必须在排序的过程中根据要求不断地在内、外存之间移动的排序
插入排序
介绍略
- 空间复杂度O(1)
- 平均时间复杂度O( \(n^2\) )
- 稳定,且同时适用顺序和链式
1
2
3
4
5
6
7
8
9
10
11
12/* 插入排序 */
int* Insertsort(ElemType A[], int n) {
int i, j;
for (i = 2; i < n; i++) //依次将A[2] ~A[n]插入前面己排序序列
if (A[i] < A[i - 1]) { //若A[i]关键码小于其前驱,将A[i]插入有序表
A[0] = A[i]; //复制为哨兵,A[0]不存放元素
for (j = i - 1;A[0] < A[j];--j)//从后往前查找待插入位置
A[j + 1] = A[j]; //向后挪位
A[j + 1] = A[0]; //复制到插入位置
}
return A;
}
折半插入
在已排序部分找插入点时使用二分查找,性能相对更好但复杂度不变,稳定但只适用于顺序表
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15void InsertSort_byhalf(ElemType A[], int n) {
int i, j, low, high, mid; //依次将A[2]~A[n]插入前面的巳排序序列
for (i = 2; i <= n; i++) { //将A[i]暂存到A[0]
A[0] = A[i];
low = 1;high = i - 1; //设置折半查找的范围
while (low <= high) {
mid = (low + high) / 2;
if (A[mid] > A[0]) high = mid - 1;
else low = mid + 1;
for (j = i - 1;j >= high + 1;--j)
A[j + 1] = A[j]; //统一后移元素,空出插入位置
A[high + 1] = A[0]; //插入操作
}
}
}
希尔(shell)排序
- 将表内元素以步长d1分为d1组,各组内部进行插入排序
- 取一个
d2<d1,重复上述操作,直到取到一个步长为1 - 进行插入排序
1 | void ShellSort(ElemType A[], int n) { |
- 空间复杂度O(1),当n在某个特定范围时,希尔排序的时间复杂度约为O( \(N^{1.3}\)),在最坏情况下希尔排序的时间复杂度为O( \(N^2\) )
- 当相同关键字的记录被划分到不同的子表时,可能改变相对次序,因此不稳定
- 仅适用于顺序存储
交换排序
冒泡排序
正序或逆序开始,两两排序相邻两位,一趟可以确定一个最小(大)值,最多n-1趟就能排完
1 | void BubbleSort(ElemType A[], int n) { |
- 空间复杂度O(1)
- 最坏情况下完全逆序,第i趟需要比n-i次,比较次数为 \(\sum_{i=1}^{n-1}(n-i)={\frac{n(n-1)}{2}}\),即时间复杂度O( $ N^2 $ )
- 稳定
快速排序
每次划分出以枢纽值为界的两个区间,并对左右分别递归
枢纽值可以随机确定,或取三个元素中值来保证期望复杂度为nlogn,常用第一个元素
1 | int Partition(ElemType A[], int low, int high) { //一趟划分 |
- 空间复杂度由于涉及栈,平均为logn,最坏O(N)
- 时间复杂度同理,但相对来说,最坏情况可能性较低,因此平均性能为内部排序算法最佳
- 划分时,若右端区间有两个关键字相同,且均小于基准值的记录,则在交换到左端区间后,它们的相对位置会发生变化,因此不稳定
选择排序
简单选择排序
每次选择第i小关键字和第i个元素交换,进行n-1次 1
2
3
4
5
6
7
8void SelectSort(ElemType A[], int n) {
for (int i = 0; i < n - 1; i++) { //一共进行 n-1 趟
int min = i; //记录最小元素位置
for (int j = i + 1; j < n; j++) //在A[i~n-1]中选择最小的元素
if (A[j] < A[min]) min = j; //更新最小元素位置
if (min != i) swap(A[i], A[min]); //swap()函数共移动元素 3 次
}
}
- 空间复杂度O(1)
- 比较次数必为n(n-1)/2,时间复杂度固定O( \(N^2\) )
- 在第i趟找到最小元素后,和第i个元素交换,可能会导致第i个元素与其含有相同关键字元素的相对位置发生改变,因此不稳定
堆排序
极大(小)堆的概念略,以极小堆为例的基本操作:
- 向上维护:直到该节点大于等于父节点,不断将其与父节点交换
- 向下维护:直到该节点小于其两个子节点,与一个比它大的子节点交换
- 构建:对一个数组从中点开始到起点向下维护
- 删除顶部节点:顶部节点与数组最后节点交换,然后对交换后的顶部节点向下维护
- 插入节点:插入的节点到数组尾部,对其向上维护
1 | void Swap(ElemType A[], int i, int j); |
堆排序就是不断移除首部节点的过程
- 空间复杂度O(1)
- 建堆的时间复杂度为O(N),每次移除top并维护平均需要logN复杂度,因此最好、最坏和平均情况下,堆排序的时间复杂度为O(Nlog2N)
- 进行筛选时,有可能把后面相同关键字的元素调整到前面,因此不稳定
归并排序
等长划分数组,然后排序,如此不断递归
1 | ElemType* B; //辅助数组 B |
就2路归并排序来说:
- 空间复杂度O(N)
- 需要logn趟归并,每次O(N),因此时间复杂度是O(NlogN)
- Merge()操作不会改变相同关键字记录的相对次序,因此稳定
- 比较次数的数量级与序列的初始状态无关
对于N个元素进行k路归并排序时,排序的趟数m满足 \(k^{m}=N\)
基数排序
根据r进制的每位数字,从高位或低位开始以此排序,最后就能得到有序数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45/* 获取元素 num 的第 k 位,其中 exp = 10^(k-1) */
int digit(int num, int exp) {
// 传入 exp 而非 k 可以避免在此重复执行昂贵的次方计算
return (num / exp) % 10;
}
/* 计数排序(根据 nums 第 k 位排序) */
void countingSortDigit(vector<int>& nums, int exp) {
// 十进制的位范围为 0~9 ,因此需要长度为 10 的桶数组
vector<int> counter(10, 0);
int n = nums.size();
// 统计 0~9 各数字的出现次数
for (int i = 0; i < n; i++) {
int d = digit(nums[i], exp); // 获取 nums[i] 第 k 位,记为 d
counter[d]++; // 统计数字 d 的出现次数
}
// 求前缀和,将“出现个数”转换为“数组索引”
for (int i = 1; i < 10; i++) {
counter[i] += counter[i - 1];
}
// 倒序遍历,根据桶内统计结果,将各元素填入 res
vector<int> res(n, 0);
for (int i = n - 1; i >= 0; i--) {
int d = digit(nums[i], exp);
int j = counter[d] - 1; // 获取 d 在数组中的索引 j
res[j] = nums[i]; // 将当前元素填入索引 j
counter[d]--; // 将 d 的数量减 1
}
// 使用结果覆盖原数组 nums
for (int i = 0; i < n; i++)
nums[i] = res[i];
}
/* 基数排序 */
void radixSort(vector<int>& nums) {
// 获取数组的最大元素,用于判断最大位数
int m = *max_element(nums.begin(), nums.end());
// 按照从低位到高位的顺序遍历
for (int exp = 1; exp <= m; exp *= 10)
// 对数组元素的第 k 位执行计数排序
// k = 1 -> exp = 1
// k = 2 -> exp = 10
// 即 exp = 10^(k-1)
countingSortDigit(nums, exp);
}
- 空间复杂度为O(r)
- 时间复杂度为O(d(N+r)),与序列的初始状态无关(d为趟数),与序列的初始状态无关
- 只要对相同位排序时使用的算法稳定,就稳定,除了常用的计数排序,也可以直接链接
内部排序小结
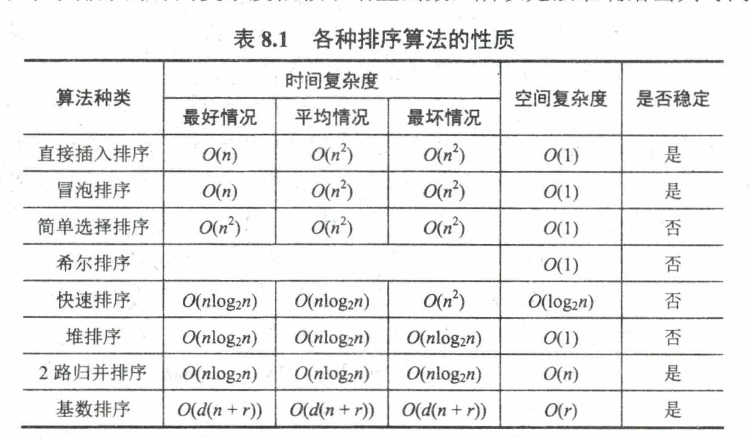
- 若n较小,可采用直接插入排序或简单选择排序
- 若初始状态基本有序,则选用直接插入或冒泡排序较好
- 若n较大,快速排序、堆排序或归并排序较好,需要稳定时只能使用归并
- 若n很大,记录的关键字位数较少且可以分解时,基数排序较好
- 比较排序的决策树是完全二叉树,因此高度h>=lg(叶节点数),叶结点数是排列数量,即n!,因此下界是nlogn
外部排序
指待排序文件较大,内存无法完全存放,需存放在外存的文件的排序
通常采用归并排序法,分为两步:
- 根据内存缓冲区大小,将外存上的文件分成若干长度为l的子文件,依次读入内存并利用内部排序方法对它们进行排序,并将排序后得到的有序子文件重新写回外存,称这些有序子文件为归并段或顺串
- 对这些归并段进行逐趟归并,直至得到整个有序文件
外部排序的总时间=内部排序所需的时间+外存信息读写的时间+内部归并所需的时间
增加路数可以显著减少IO
在k个元素中选择关键字最小的记录需要比较k-1次。每趟归并n个元素需要做(n-1)(k-1)次比较,则S趟归并总共需要的比较次数为:
\(S(n-1)(k-1)=\left \lceil \log_{k}r\right \rceil (n-1)(k-1)=\left \lceil \log_{2}r \rceil(n-1)(k-1)/\lceil\log_{2}k\right\rceil\)
为了使内部归并不受k的增大的影响,引入了败者树,k个叶结点分别存放k个归并段在归并过程中当前参加比较的记录,内部结点用来记忆左右子树中的"失败者”,而让胜者往上继续进行比较,一直到根结点。
若比较两个数,大的为失败者、小的为胜利者,则根结点指向的数为最小数
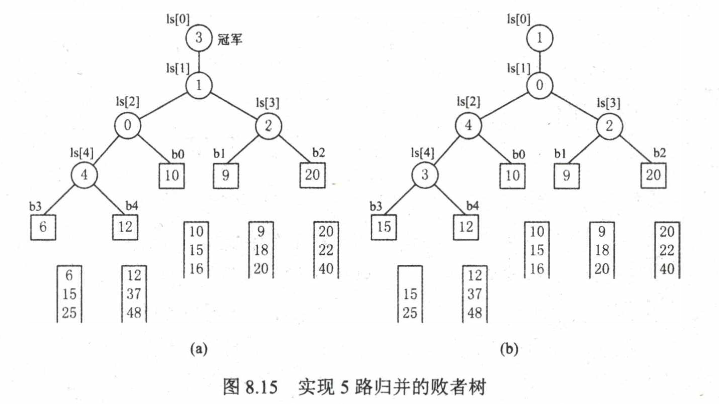
k个记录中选择最小关键字,最多需要 \(\lceil\log_2^{k}\rceil\) 次比较(败者树深度为比较次数+1)。所以总的比较次数为:
\(S(n-1)\left\lceil\log_{2}\!k\right\rceil=\left\lceil\log_{k}\!r\right\rceil(n-1)\left\lceil\log_{2}\!k\right\rceil=(n-1)\left\lceil\log_{2}r\right\rceil\)
使用败者树时,内部归并的比较次数与k无关,只要内存空间允许,增大归并路数上将有效地减少归并树的高度,减少I/O次数,提高速度
置换-选择排序
用来产生更长的初始归并段,减少段个数r,从而减少归并趟数S
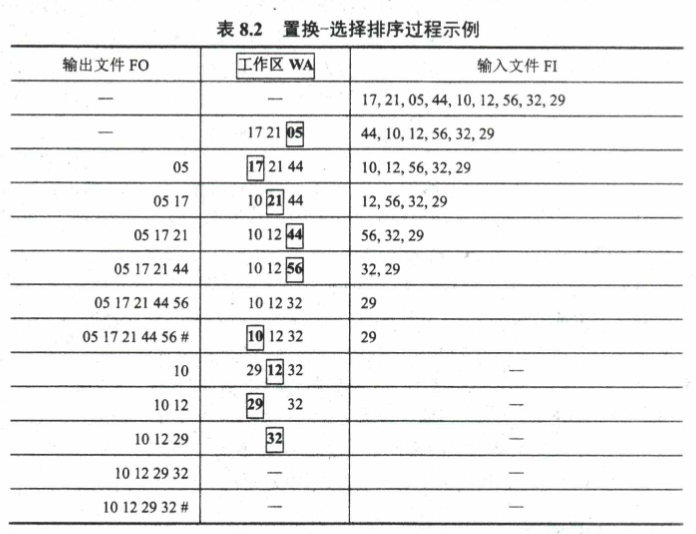
设初始待排文件为FI初始归并段输出文件为FO,内存工作区为WA, FO和WA的初始状态为空,WA可容纳w个记录:
- 从FI输入w个记录到工作区WA
- 从WA中选出其中关键字取最小值的记录,记为MINIMAX记录(选择MINIMAX记录的过程用败者树实现)
- 将MINIMAX记录输出到FO中去
- 若FI不空,则从FI输入下一个记录到WA中
- 从WA中所有关键字比MINIMAX记录的关键字大的记录中选出最小关键字记录(使用败者树),作为新的MINIMAX记录
- 重复3.~5.直至在WA中选不出新的MINIMAX记录为止,由此得到一个初始归并段,输出一个归并段的结束标志到F0中去
- 重复2.~6.直至WA为空。由此得到全部初始归并段
最佳归并树
将哈夫曼树的思想推广到m叉树的情形,在归并树中,让记录数少的初始归并段最先归并,记录数多的初始归并段最晚归并,就可以建立总的I/O次数最少的最佳归并树
若初始归并段不足以构成一棵严格k叉树时,需添加长度为0的"虚段"
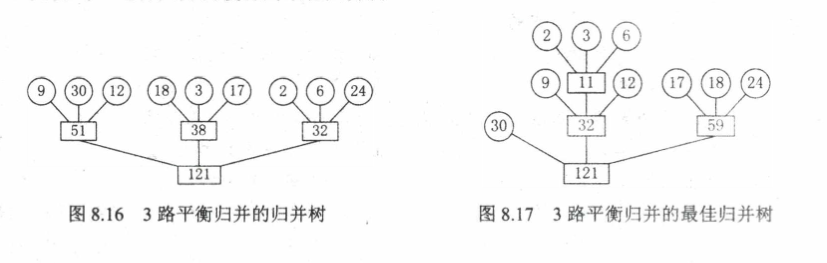
设度为0的结点有n0个,度为k的结点有nk个,归并树的结点总数为n,则:
- n=nk + n0; n=k.nk + 1
- 对严格k叉树有 \(n_0=(k-1)n_k+1\) ,由此可得 \(n_k=(n0-1)/(k- 1)\)
- 若 \((n_{0}-1)\%(k-1)==0\),则说明这n0个叶结点(初始归并段)正好可以构造k叉归并树。此时,内结点有nk个
- 若 \((n_{0}-1)\%(k-1)=u\ne0\) ,则对于这n0个叶结点,其中有u个多余,不能包含在k叉归并树中,应在原有个nk内结点的基础上再增加1个内结点
- 添加的节点取代叶节点,加上k-u-1个空归并段可以构成一颗归并树
- 每次冒泡排序后可以检查是否已经有序
- 对n个关键字进行快速排序,最多递归n次,最少logn次(二分)
- 取一大堆数据中的k个最大(最小)的元素时,优先采用堆排序
- 堆删除一个元素后,除了向下比较,还要比较左右两个子节点的大小关系,选择一个子树向下递归
- 将两个各有N个元素的有序表合并,最少比N次,最多2N-1次
- 带权连通图的任意一个环中所包含的边的权值均不相同时,其MST(最小(代价)生成树)唯一